A comparative study of adaptive dose-finding designs for phase I oncology trials of combination therapies

Abstract

Little is known about the relative performance of competing model-based dose-finding methods for combination phase I trials. In this study, we focused on five model-based dose-finding methods that have been recently developed. We compared the recommendation rates for true maximum-tolerated dose combinations (MTDCs) and over-dose combinations among these methods under 16 scenarios for 3 × 3, 4 × 4, 2 × 4, and 3 × 5 dose combination matrices. We found that performance of the model-based dose-finding methods varied depending on (1) whether the dose combination matrix is square or not; (2) whether the true MTDCs exist within the same group along the diagonals of the dose combination matrix; and (3) the number of true MTDCs. We discuss the details of the operating characteristics and the advantages and disadvantages of the five methods compared.

1. Introduction

Phase I trials in oncology are conducted to identify the maximum tolerated dose (MTD), which is defined as the highest dose that can be administered to a population of subjects with acceptable toxicity. A model-based dose-finding approach is efficient in locating the MTD in phase I trials. The continual reassessment method (CRM) [1] has provided a prototype for such an approach in single-agent phase I trials. Many other dose-finding methods have been developed for single-agent phase I trials, while in recent years, two-agent combination trials have also attracted significant attention. In two-agent combination phase I trials, we need to capture the dose-toxicity relationship for the combinations and identify a MTD combination (MTDC). To accommodate this requirement, many authors have developed combination dose-finding methods, an overview of which is given in Harrington et al. [2]. Some of these published methods can be classified as rule-based or algorithm-based designs [3–5]. A recent editorial in Journal of Clinical Oncology by Mandrekar [6] described the use of the method of Ivanova and Wang [3] in a phase I study of neratinib in combination with temsirolimus in patients with human epidermal growth factor receptor 2-dependent and other solid tumors [7]. Recently, Riviere et al. [8] compared two algorithm-based and four model-based dose-finding methods using three evaluation indices under 10 scenarios of a 3 × 5 dose combination matrix. Among their conclusions was that the model-based methods performed better than the algorithm-based ones, as has been demonstrated in single-agent studies [9].

A key assumption to phase I methods for single-agent trials is the monotonicity of the dose-toxicity curve. In this case, the curve is said to follow a ‘complete order’ because the ordering of probabilities of dose-limiting toxicity (DLT) for any pair of doses is known and administration of greater doses of the agent can be expected to produce DLTs in increasing proportions of patients. In studies testing combinations, the probabilities of DLT often follow a ‘partial order’ in that there are pairs of combinations for which the ordering of the probabilities is not known. One approach taken in early work in model-based dose finding for drug combinations was to reduce the problem to a complete order by laying out an a priori ordering of the combinations, where the initial ordering is based on single agent toxicity profiles. Korn and Simon [10] present a graphical method, called the ‘tolerable dose diagram’, based on single agent toxicity profiles, for guiding the escalation strategy. Kramar et al. [11] also lay out an a priori ordering for the combinations and estimate the MTDC using a parametric model for the probability of a DLT as a function of the doses of the two agents. The disadvantage of this approach is that it limits the number of combinations that can be considered and could produce highly misleading results if the assumed ordering is incorrect. More recent methods have moved away from reducing the two-dimensional dose-finding space to a single dimension. Thall et al. [12] proposed a six-parameter model for the toxicity probabilities in identifying a toxicity equivalence contour for the combinations. Wang and Ivanova [13] proposed a logistic-type regression that used the doses of the two agents as the covariates. The papers by Thall et al. [12] and Wang and Ivanova [13] differ from Korn and Simon [10] and Kramar et al. [11] in their view of what constitutes a ‘MTD’ for a combination. By specifying a prior ordering, Korn and Simon [10] and Kramar et al. [11] produce a single MTDC that is estimated to have acceptable toxicity. Thall et al. [12] and Wang and Ivanova [13] note that unlike the completely ordered (monotone) case, there is no unique MTDC. The set of combinations with acceptable toxicity forms an equivalence contour in two dimensions.

Our focus here is on model-based dose-finding methods for combinations, in which the primary interest is to find only one MTDC for recommendation in phase II studies. To this end, Conaway et al. [14] estimated the MTDC by determining the complete and partial orders of the toxicity probabilities by defining nodal and non-nodal parameters. A nodal parameter is one whose ordering is known with respect to all other parameters. Although the method of Conaway et al. [14] does not rely on a parametric dose-toxicity model, it is not an algorithmic-based or rule-based design, so we choose to consider it in the set of model-based approaches. This method was implemented in a phase I trial investigating induction therapy with Velcade (Takeda Pharmaceuticals International Corporation, Cambridge, MA, USA) and Vorinostat in patients with surgically resectable non-small cell lung cancer [15]. Yin and Yuan [16, 17] developed Bayesian adaptive designs based on latent 2 × 2 tables [16] and a copula-type model [17] for two agents. Braun and Wang [18] proposed a hierarchical Bayesian model for the probability of toxicity of two agents. Wages et al. [19, 20] developed both Bayesian [19] and likelihood-based [20] designs that laid out possible complete orderings associated with the partial order and used model selection techniques and the CRM to estimate the MTDC. Hirakawa et al. [21] proposed a dose-finding method based on the shrunken-predictive probability of toxicity for combinations. Some authors have compared their method with existing model-based methods [19–21]. Wages et al. [20] reported that their method was competitive with the previously proposed method of Wages et al. [19], which has been demonstrated to have a comparable performance to the methods of Conaway et al. [14] and Yin and Yuan [16, 17]. Hirakawa et al. [21] reported that their method was competitive with the methods of Yin and Yuan [17] and Wages et al. [20].

These comparisons have been made under limited and ideal settings with respect to the type of combination matrix, the position and number of true MTDCs, using few evaluation indices, and often for large sample sizes (i.e., ≈ 60). However, in practice, we often encounter complex and various settings of phase I trials as shown later in Section 3.1. Specifically, (1) the dose combination matrices are not only square type (i.e., 3 × 3 and 4 × 4) but also rectangle one (2 × 4 and 3 × 5); (2) the underlying position and number of true MTDCs are possibly various; and (3) the sample size is as small as 30 in practice. Furthermore, the operating characteristics of the dose-finding methods developed based on different principles should be compared based on many evaluation indices. In this paper, we examine performance of five methods based on six evaluation indices under 16 toxicity scenarios. In general, our goal is to evaluate (1) how well each method identifies MTDC’s at and around the target rate; (2) how well each method allocates patients to combinations at and around the true MTDC; and (3) how feasible is it to implement each method given its respective prior specifications and software capabilities. We organize the results by the types of dose-combination matrix and the position and number of true MTDCs. We provide some recommendations on the use of the five model-based dose-finding methods for practitioners who design a phase I trial with some discussions about the rationale for the performance differences among the methods.

The compared methods can be roughly categorized into two groups: (1) those using a flexible model, with/without an interaction term, to jointly model the DLT probability at each dose pair of the two agents and (2) those that take a more underparameterized approach, relying upon single-parameter ‘CRM-type’ models and/or order-restricted inference [22]. For those in group (1), we focus on the method based on a copula-type [17] model, termed the YYC. We also evaluate the method using a hierarchical Bayesian model [18], termed the BW method. Finally, we evaluate the likelihood-based dose-finding method using a shrinkage logistic model [21], termed the HHM method. For those methods in group (2), we choose likelihood-based CRM for partial ordering [20], termed the WCO method and the order-restricted inference method of Conaway et al. [14], which we term CDP. This will be the first time, to our knowledge, that CDP will be compared to competing methods in a drug combination matrix setting. Of course there are other methods that have been left out of this comparison such as latent contingency table approach of Yin and Yuan [16] and a recent method by Braun and Jia [23]. However, we have included at least one method by these authors in our comparison, and the included methods have the advantage of having user-friendly software available on the web. During review of this manuscript, Riviere et al. [24] proposed a Bayesian dose-finding design based on the logistic model, while Mander and Sweeting [25] published a curve-free method that relies on the product of independent beta probabilities.

In the simulation studies, we compared the recommendation rates for true MTDCs and overdose combinations (ODCs). Average number of patients allocated to true MTDCs, overall percentage of observed toxicities, average number of patients allocated to a dose combination above the true MTDCs, and an index that reflects a design’s accuracy were also evaluated. The designs vary in terms of (1) whether they are one-stage or two-stage; (2) the nature of their start-up rules/initial escalation schemes; and (3) the characteristics of their dose-finding algorithms. We wanted to keep these aspects of the methods as close as possible to the published work, so as to be true to the original design intended by the authors. We feel that, if every design aspect of each method were the same, the results would essentially be reduced to a comparison of dose-response models. Our goal is to compare the dose-finding designs proposed by these published methods. The remainder of this paper is organized as follows. We describe the motivating examples in the remainder of this section. We summarize the five model-based dose-finding methods we compared in Section 2 and compare the operating characteristics through simulation studies in Section 3. Finally, some discussions will appear in Section 4.

2. Dose-finding methods compared

In this section, we overview the five dose-finding methods we compared. The methodological characteristics of each design are summarized in Table I. The YYC and BW methods have been developed based on Bayesian inference, while the HHM and WCO methods are based on likelihood inference. The approach of CDP is based on the estimation procedure of Hwang and Peddada [26]. The YYC and HHM methods model the interactive effect of two agents on the toxicity probability, but the BW method does not. The WCO method is based on the CRM and uses a class of underparameterized working models based on a set of possible orderings for the true toxicity probabilities. In terms of the restriction on skipping dose levels, the BW method allows the simultaneous escalation or de-escalation of both agents, whereas the YYC, CDP, and HHM methods do not. On the other hand, the WCO method allows a flexible movement of dose levels throughout the trial and does not restrict movement to ‘neighbors’ in the two-agent combination matrix.

Table I.

Methodological characteristics of the five dose-finding methods we compared.

Method	YYC	CDP	BW	WCO	HHM
Estimation	Bayesian	Hwang and Peddada [26]	Bayesian	Likelihood	Likelihood
Parametric dose-toxicity model	Copula	None	Hierarchical	Power	Shrinkage
Prior toxicity probability specification	Yes	No	Yes	Yes	No
Inclusion of interactive effect in the model	Yes	No	No	No	Yes
Cohort size used in the original paper	3	1	1	1	3
Restriction skipping on dose levels	One dose level of change only and not allowing a simultaneous escalation or de-escalation of both agents	Same as the YYC method	One dose level of change only but allowing a simultaneous escalation or de-escalation of both agents	No skipping restriction	Same as the YYC method

YYC, Yin and Yuan [17]; CDP, Conaway, Dunbar, and Peddada [14]; BW, Braun and Wang [18]; WCO, Wages, Conaway, and O’Quigley [20]; HHM, Hirakawa, Hamada, and Matsui [21].

In this section, we introduce both the statistical model for capturing the dose-toxicity relationship and the dose-finding algorithm for exploring the MTDCs because almost all of the dose-finding methods for two-agent combination trials have been often developed by improving or devising these components of the method. The other detailed design characteristics are not shown in this paper. We considered a two-agent combination trial using agents A_j (j = 1, …, J), and B_k (k = 1, …, K), respectively, throughout. We denote the probability of DLT by π and the targeting toxicity probability specified by physicians by ϕ. The other symbols are independently defined by the dose-finding methods we compared.

2.1. Bayesian approach based on copula-type regression (YYC)

Yin and Yuan [17] introduced Bayesian dose-finding approaches using copula-type models. Let p_j and q_k be the pre-specified toxicity probability corresponding to A_j and B_k, respectively, and subsequently $p_j^{\alpha }$ and $q_k^{\beta }$ be the modelled probabilities of toxicity for agents A and B, respectively, where α > 0 and β > 0 are unknown parameters. Let the true probability of DLT at combination (A_j, B_k) be denoted π_jk. Yin and Yuan [17] proposed to use a copula-type regression model in the form of

$${\pi }_{jk}=1-{\{{(1-p_j^{\alpha })}^{-\gamma }+{(1-q_k^{\beta })}^{-\gamma }-1\}}^{-1/\gamma },$$

where γ > 0 characterizes the interaction of two agents (i.e., the YYC method). Several authors have recently provided a more in-depth discussion on multiple binary regression models for dose-finding in combinations [27–29]. Using the data obtained at that time, the posterior distribution is obtained by

$$f(\alpha ,\beta ,\gamma |\text{Data})\propto L(\alpha ,\beta ,\gamma |\text{Data})f(\alpha )f(\beta )f(\gamma ),$$

where L(α, β, γ|Data) is the likelihood function of the model and f(α), f(β), and f(γ) are prior distributions, respectively.

2.1.1. Prior specifications in YYC

In performing YYC, we need to elicit the prior toxicity probabilities p_j and q_k from investigators. In two-agent combination phase I trials, the highest dose level of each agent would be often the MTD that has been identified in each monotherapy phase I trial; therefore, it is reasonable to set the prior toxicity probability of p_J (or q_K) equal to the target ϕ (i.e., 0.30). The remaining toxicity probabilities (p₁, …, p_J−1 and q₁, …, p_K−1) could be based on the investigators’ elicitations, but a recent publication by Yin and Lin [30] recommended taking an even distribution from 0 to ϕ. We also need to specify the hyperparameters α, β, and γ. Although we cannot change them in the software released by Yin and Yuan [17], they had examined the sensitivity of operating characteristics for α and β and reported that YYC is robust for different hyperparameter values. The Gamma(2, 2) priors for α and β and the Gamma(0.1, 0.1) prior on γ are further recommended for the Clayton-type copula by Yin and Lin [30].

2.1.2. Dose-finding algorithm in YYC

Let c_e and c_d be the fixed probability cut-offs for dose escalation and de-escalation, respectively. Yin and Yuan [17] indicate that their dose-finding algorithm may be difficult to implement early in the trial because of limited available data.

Start-up rule

1. Treat patients along the vertical dose escalation in the order of {(A₁, B₁), (A₁, B₂), …} until the first DLT is observed.

2. Next, treat patients along the horizontal dose escalation in the order of {(A₂, B₁), (A₃, B₁), …} until the first DLT is observed.

3. As long as one DLT is observed in both the vertical and horizontal directions, then the Bayesian dose finding will be started.

After the start-up rule for stabilizing parameter estimation, we move to the following model-based dose-finding stage based on the posterior probability of π_jk for the rest of the trial. In this stage, dose escalation or de-escalation is restricted to one dose level of change only while not allowing a transition along the diagonal direction (corresponding to simultaneous escalation or de-escalation of both agents).

1. If at the current dose combination (j, k), Pr(π_jk < ϕ) > c_e, the dose is escalated to the aforementioned adjacent dose combination with the probability of toxicity higher than the current value and closest to ϕ. If the current dose combination is (A_J, B_K), the doses remain at the same levels.

2. If at the current dose combination (j, k), Pr(π_jk > ϕ) > c_d, the dose is de-escalated to the adjacent dose combination with the probability of toxicity lower than the current value and closest to ϕ. If the current dose combination is (A₁, B₁), the trial is terminated.

3. Otherwise, the next cohort of patients continues to be treated at the current dose combination (doses staying at the same levels).

4. Once the maximum sample size N_max has been achieved, the dose combination that has the probability of toxicity that is closest to ϕ is selected as the MTDC.

2.2. A hierarchical Bayesian design (BW)

Braun and Wang [18] developed a novel hierarchical Bayesian design for combination trials. Let a_j and b_k be the dose levels corresponding to A_j and B_k respectively and the values of which are not the actual clinical values of the doses but are the ‘effective’ dose values that will lend stability to their dose-toxicity model. It is assumed that each π_jk has a beta distribution with parameters α_jk and β_jk. Notably, α_jk(β_jk) can be interpreted as the prior number of patients assigned to combination (j, k) expected to have (not have) a DLT. Braun and Wang [18] proposed to model α_jk and β_jk using the parametric functions of a_j and b_k,

$$\text{log}\{{\alpha }_{jk}(\theta )\}={\theta }_0+{\theta }_1{a}_j+{\theta }_2{b}_k\text{ and log}\{{\beta }_{jk}(\lambda )\}={\lambda }_0-{\lambda }_1{a}_j-{\lambda }_2{b}_k,$$

respectively, where θ = {θ₀, θ₁, θ₂ } has a multivariate normal distribution with mean μ = {μ₀, μ₁, μ₂ }, λ = {λ₀, λ₁, λ₂} has a multivariate normal distribution with mean ω = {ω₀, ω₁, ω₂ }, and both θ and λ have variance σ²I₃, in which I₃ is 3 × 3 identity matrix. The samples from the posterior distribution for (θ, λ) are easily obtained using Markov chain Monte Carlo methods. These samples lead to posterior distributions for each element of θ and λ, which, in turn, lead to a posterior distribution for each π_jk. The corresponding posterior means π̄_jk are calculated.

The BW method necessitates careful elicitation of priors and effective dose values. Development of priors begins with the specification of p_j1 and q_1k, which are a priori values for the E(π_j1) and E(π_1k). Braun and Wang [18] set the lowest dose of each agent to zero, that is, a₁ = b₁ = 0. Consequently, log(α₁₁) = θ₀ and log(β₁₁) = λ₀ so that θ₀ and λ₀ describe the expected number of DLTs for combination (A₁, B₁) and the remaining parameters in θ and λ will describe how the expected DLTs for other combinations relate to (A₁, B₁). Braun and Wang [18] also used the fact that

$$\frac{K{p}_{11}}{K(1-p_{11})}=\frac{{\alpha }_{11}}{{\beta }_{11}}=\frac{\text{exp}\{{\theta }_0\}}{\text{exp}\{{\varphi }_0\}}=\frac{\text{exp}\{{\mu }_0\}}{\text{exp}\{{\omega }_0\}}.$$

Then, the prior values for μ₀ and ω₀ are obtained via

$${\mu }_0=\text{log}(K{p}_{11})\text{ and }{\omega }_0=\text{log}(K[1-p_{11}]),$$

where K = 1000 was chosen as a scaling factor to keep both hyperparameters sufficiently above 0. Further, Braun and Wang [18] select ${\mu }_1={\mu }_2={\omega }_1={\omega }_2=2\sqrt{{\sigma }^2}$ so that 97.5% of the prior distributions for θ₁, θ₂, λ₁ and λ₂ will lie above 0, depending upon the value ofσ². The authors point out that a value in the interval [5, 10] is often sufficient in their settings for adequate operating characteristics but each trial setting will require fine tuning of σ². Braun and Wang [18] further define elicited odds ratios that can be approximated by

$${\tilde{\xi }}_{j·}\approx \text{exp}\{({\mu }_1+{\omega }_1)a_j\}\text{ and }{\tilde{\xi }}_{·k}\approx \text{exp}\{({\mu }_2+{\omega }_2)b_k\},$$

in which effective dose values are obtained by solving for a_j and b_k. All doses are rescaled to be proportional to log-odds ratios relative to combination (A₁, B₁). The developments priors and effective dose values in BW are somewhat complex, and it is recommended to read the original paper of BW for further detail.

2.2.1. Prior specifications in BW

As in YYC, we need to elicit the toxicity probability parameter p_j1 and q_1k from investigators. As we described in the previous section of YYC, the values for p_J1 and q_1K are set to 0.3, and the toxicity probabilities of all dose combinations are set arithmetically (as you seen in Table 3) in the simulation studies. We assessed operating characteristics of BW using three different values of σ², that is, σ² = {3, 5, 10}. The best overall performance was obtained using σ² = 3, which we present in our results, while BW for σ² = 5 (or 10) performed less well under the scenarios we selected. We are happy to share these additional results with any interested reader. This indicates that we need to fine-tune the value of σ² in practice, as Braun and Wang [18] have suggested.

Table III.

Prior toxicity probabilities we used in the simulation studies in the Braun and Wang (BW) method.

	A
		1	2	3	4	5	1	2	3	4	5
				3 ×3					4× 4
B	4						0.30	0.375	0.45	0.525
	3	0.30	0.40	0.50			0.225	0.30	0.375	0.45
	2	0.20	0.30	0.40			0.15	0.225	0.30	0.375
	1	0.10	0.20	0.30			0.075	0.15	0.225	0.30
				2 ×4					3× 5
	3						0.30	0.35	0.40	0.45	0.50
	2	0.30	0.35	0.40	0.45		0.20	0.25	0.30	0.35	0.40
	1	0.15	0.20	0.25	0.30		0.10	0.15	0.20	0.25	0.30

2.2.2. Dose-finding algorithm in BW

The BW method accrues all patients in a single stage, rather than in two stages. The dose-finding algorithm is similar to that of the YYC method after the YYC start-up rule.

1. The first subject is assigned to combination (A₁, B₁).

2. Compute a 95% CI for the overall DLT rate among all combinations using the cumulative number of observed DLTs for subjects 1, 2, …, (i−1). If the lower bound of the CI is greater than the target DLT rate, ϕ, terminate the trial.

3. Otherwise, use the outcomes and assignments of subjects 1, 2, …, (i−1) to determine the posterior distribution of each π_jk, with posterior means π̄_jk.

4. Extract the set of dose combinations, that is,

   $$S=\{(j,k)|j_{i-1}-1⩽j⩽j_{i-1}+1,k_{i-1}-1⩽k⩽k_{i-1}+1\}$$

   that contains combinations that are within one-dose level of the corresponding doses in the combination assigned to the most recently enrolled patient (1, 2, ⋯, (i−1)) and subsequently allocate the dose combination (j*, k*) in S as the one with the smallest |π̄_jk − ϕ| to the next patient i.

5. We repeat these steps until maximum sample size N_max is reached.

2.3. Approach using a shrinkage logistic model (HHM)

Hirakawa et al. [21] developed a dose-finding method based on the shrinkage logistic model. Hirakawa et al. [21] first model the joint toxicity probability π_i for patient i using an ordinary logistic regression model with a fixed intercept β₀, as follows:

$${\pi }_i=\frac{\text{exp}({\beta }_0+{\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+{\beta }_3{x}_{i3})}{1+\text{exp}({\beta }_0+{\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+{\beta }_3{x}_{i3})},$$

where x_i1 and x_i2 are the actual (or standardized) dose levels of agents A and B, respectively, and x_i3 represents a variable of their interaction such that x_i3 = x_i1 × x_i2 for patient i.

Using the maximum likelihood estimates (MLEs) for the parameters β̂_j (j = 1, 2, 3), Hirakawa et al. [21] proposed the shrunken predictive probability (SPP):

$${\tilde{\pi }}_i=\frac{\text{exp}({\beta }_0+(1-{\delta }_1){\hat{\beta }}_1{x}_{i1}+(1-{\delta }_2){\hat{\beta }}_2{x}_{i2}+(1-{\delta }_3){\hat{\beta }}_3{x}_{i3})}{1+\text{exp}({\beta }_0+(1-{\delta }_1){\hat{\beta }}_1{x}_{i1}+(1-{\delta }_2){\hat{\beta }}_2{x}_{i2}+(1-{\delta }_3){\hat{\beta }}_3{x}_{i3})},$$

where the shrinkage multiplier 1 − δ_j (j = 1, 2, and 3) is a number between 0 and 1. Hirakawa et al. [21] also developed the estimation method of the shrinkage multipliers.

2.3.1. Dose-finding algorithm in HHM

Hirakawa et al. [21] invoke the following start-up rule-based dose allocation algorithm with the cohort size of 3 until the MLE for each parameter is obtained. After obtaining the MLEs for the regression parameters, we calculate the SPP of toxicity for the current dose combination d_c. We adopt the same restriction on skipping dose level proposed by the YYC method. Let c₁ and c₂ be the allowable bands from the target toxicity limit ϕ as MTDCs.

Start-up rule

1. The matrix of combinations is zoned according to its diagonals from the upper left entry to the lower right entry, as described in the WCO method.

2. The first cohort is allocated to the zone that includes the lowest dose combinations (A₁, B₁). If a prespecified stopping rule is met, we terminate the trial for safety. Otherwise, we would escalate to the next zone. If more than one dose combination is contained within a particular zone, we can sample without replacement from the dose combinations available, allocating the sampled dose combination to the next cohort. This sampling and allocation step is continued until all available dose combinations in that zone are tested.

3. During the aforementioned step, the existence of MLEs for the regression coefficients is checked for every cohort of three patients, although we do not show this procedure in detail in this paper. If we obtain the MLEs, the SPP of toxicity for each dose combination is calculated, and subsequently the following dose-finding algorithm is applied.

Following the start-up rule, Hirakawa et al. [21] proposed the following dose-finding algorithm:

1. If at the current dose combination d_c, ϕ − c₁ ⩽ π̃(d_c) ⩽ ϕ + c₂, the next cohort of patients continues to be allocated to the current dose combination.

2. Otherwise, the next cohort of patients is allocated to the dose combination with the SPP closest to ϕ among the adjacent or current dose combinations.

3. Once the maximum sample size N_max is reached, then dose combination that should be assigned to the next cohort is selected as the MTDC. In addition, if we encounter the situation where d_c = d₁ and p̃(d_c) > ϕ + c₂, we terminate the trials for safety.

2.4. Design based on order restricted inference (CDP)

The method proposed by Conaway et al. [14] is based on the estimation procedure of Hwang and Peddada [26]. Parameter estimation subject to order restrictions is discussed in Hwang and Peddada [26] and Dunbar, Conaway, and Peddada [31]. The method of Hwang and Peddada [26] uses different estimation procedures for ‘nodal’ and ‘non-nodal’ parameters. For nodal parameters, estimation proceeds by establishing a simple order that is consistent with the partial order. This is performed by guessing the unknown inequalities and obtaining isotonic regression estimates of the nodal parameters π_jk based on the pool adjacent violators algorithm (PAVA). In order to estimate the non-nodal parameters, Hwang and Peddada [26] eliminate the smallest number of parameters that make a non-nodal parameter into a nodal parameter. For instance, in a J × K matrix of drug combinations, π₁₂ is a non-nodal parameter because it is unknown whether π₁₂ < π₂₁ or vice versa. Estimates of the non-nodal parameters can be obtained using a version of PAVA for simple orders that fix the nodal parameters at their previously estimated values. Hwang and Peddada [26] show that the resulting estimates satisfy the partial order. Conaway et al. [14] computed estimates of the parameters under all possible guesses and averaged them in order to eliminate the dependence of the estimates on a single guess at the ordering between non-nodal parameters.

The approach of Conaway et al. [14] is a two-stage design. The initial stage is designed to quickly escalate through treatment combinations that are non-toxic (in single patient cohorts until first DLT is observed), and the second stage implements the Hwang and Peddada [26] estimates. Throughout the second stage, the toxic response data for the (A_j, B_k) treatment combination is of the form Y = {Y_jk; j = 1, …, J; k = 1, …, K} with Y_jk equal to the number of observed toxicities from patients treated with combination (A_j, B_k). Let 𝒜 denote the set of treatments that has been administered thus far in the trial such that 𝒜 = {(j, k) : n_jk > 0}, where n_jk denotes the number of patients treated on each combination. Using a Beta(α_jk, β_jk) prior for the π_jk, the DLT probabilities are updated only for (j, k) ∈ 𝒜.

$${\hat{\pi }}_{jk}=\frac{Y_{jk}+{\alpha }_{jk}}{n_{jk}+{\alpha }_{jk}+{\beta }_{jk}}.$$

The estimation procedure of Dunbar et al. [31] is applied to the updated posterior means π̂_jk for (j, k) ∈ 𝒜.

2.4.1. Prior specifications in CDP

If appropriate prior information is available to investigators, it is described through a prior distribution of the form π_jk ~ Beta(α_jk, β_jk). The investigators specify the expected value of π_jk and an upper limit u_jk such that they are 95% certain that the toxicity probability will not exceed u_jk. The equations

$$E[{\pi }_{jk}]=\frac{{\alpha }_{jk}}{{\alpha }_{jk}+{\beta }_{jk}}\text{ and Pr}[{\pi }_{jk}⩽u_{jk}]=0.95$$

are solved in order to obtain prior specifications for α_jk and β_jk. Another prior specification for CDP is to choose a subset of possible dose-toxicity orders based on ordering the combinations by rows, columns, and diagonals of the drug combination matrix. Using the guidance of Wages and Conaway [32], we choose a subset of approximately 6 – 9 orderings. This provides an appropriate balance between choosing enough orderings so that we include adequate information to account for the uncertainty surrounding partially ordered dose-toxicity curves, without increasing the dimension of the problem so much so that we diminish performance. Arrange orderings according to movements across rows, up columns, and along diagonals. Because, in a large matrix, there could be many ways to arrange combinations along a diagonal, restrict movements to only moving across rows, up columns, and up or down any diagonal.

2.4.2. Dose-finding algorithm in CDP

Stage 1

The first patient is entered at the starting treatment, usually combination (A₁, B₁). The most appropriate treatment to which to escalate could possibly consist of more than one treatment combination. For example, in a matrix of combinations, the possible escalation treatments for (1, 1) are (1, 2) or (2, 1). Therefore, if no DLT is observed in (1, 1), then the next patient is treated with a combination chosen from among the ‘possible escalation treatments’. If no DLT is observed in this patient, the next patient is assigned a combination randomly chosen from the set of possible escalation treatments that have not yet been administered in the trial. Once a DLT is observed, stage 2 begins.

Stage 2

For all (j, k) ∈ 𝒜, we compute the loss, L (π̂_jk, ϕ), associated with each combination. In this paper, as in Conaway et al. [14], we implement a symmetric loss function so that L (π̂_jk, ϕ) = |π̂_jk − ϕ|.

1. Let l_min = {min_(j,k)∈𝒜 L_jk (π̂_jk, ϕ)} and let 𝒞 be the set of combinations with losses equal to the minimum observed loss, 𝒞 = {(j, k) : L_jk(π̂_jk, ϕ) = l_min}.

2. If there is a single combination, c ∈ 𝒞, then the suggested combination is c, with an estimated DLT probability of π̂_c.

3. If 𝒞 contains more than one combination, then we randomly choose from among them according to the rules:

   1. If π̂_c > ϕ ∀ c ∈ 𝒞, we randomly choose from among the set 𝒞 of candidate combinations.
   2. If π̂_c ⩽ ϕ for at least one c ∈ 𝒞, we choose randomly among the combinations in 𝒞 that are candidate for having the ‘largest’ DLT probability.

4. If the suggested combination has an estimated DLT probability that is less than the target, a combination is chosen at random from among the ‘possible escalation treatments’ that have not yet been tested in the trial.

2.5. Partial ordering continual reassessment method (WCO)

The CRM for partial orders is based on utilizing a class of working models that corresponds to possible orderings of the toxicity probabilities for the combinations. Specifically, suppose there are M possible orderings being considered which are indexed by m. For a particular ordering, we model the true probability of toxicity, π_jk, corresponding to combination A_j and B_k, via a power model

$${\pi }_{jk}\approx F_m(d_{jk},{\beta }_m)={[p_{jk}(m)]}^{{\beta }_m};\hspace{1em}m=1,\dots ,M,$$

where the p_jk(m) represents the skeleton of the model under ordering m. In an unpublished PhD thesis by Wages, the use of other working models common to the CRM class such as a hyperbolic tangent function or a logistic model was explored and found that there is little difference in the operating characteristics among the various choices of working model. We let the plausibility of each ordering under consideration be described by a set of prior probabilities τ = {τ(1), …, τ(M)}, where τ(m) ⩾ 0 and Στ(m) = 1; m = 1, …, M. Using the accumulated data, Ω_i, from i patients, the MLE β̂_m of the parameter β_m can be computed for each of the m orderings, along with the value of the log-likelihood, ℒ_m (β̂_m | Ω_i), at β̂_m. Wages et al. [19, 20] propose an escalation method that first chooses the ordering that maximizes the updated probability

$$\omega (m)=\frac{\text{exp}\left\{{ℒ}_m\right({\hat{\beta }}_m|{\mathrm{\Omega }}_i)\}\tau (m)}{\sum _{m=1}^M\text{exp}\left\{{ℒ}_m\right({\hat{\beta }}_m|{\mathrm{\Omega }}_i)\}\tau (m)}$$

before each patient inclusion. If we denote this ordering by m*, the authors use the estimate β̂_m* to estimate the toxicity probabilities for each combination under ordering m* so that π̂_jk ≈ F_m* (d_jk, β̂_m*).

Prior specifications in WCO

As in CDP, a prior specification for WCO is to choose a subset of possible dose-toxicity orders. We again rely on the guidance of Wages and Conaway [32] and choose approximately 6 – 9 orderings based on ordering the combinations by rows, columns, and diagonals of the drug combination matrix. Another specification that needs to be made prior to beginning the study is a set of skeleton values p_jk(m). We can rely on the algorithm of Lee and Cheung [33] to generate reasonable skeleton values using the function getprior in R package dfcrm. We simply need to specify skeleton values at each combination that are adequately spaced [34] and adjust them to correspond to each of the possible orderings, in order for WCO to have good performance in terms of identifying an MTDC. The location of these skeleton values can be adjusted to correspond to each of the possible orderings using the getwm function in R package pocrm [35].

2.5.1. Dose-finding algorithm in WCO

Within the framework of sequential likelihood estimation, an initial escalation scheme is needed, because the likelihood fails to have a solution on the interior of the parameter space unless some heterogeneity (i.e., at least one toxic and one non-toxic) in the responses has been observed.

Stage 1

In the first stage, WCO makes use of ‘zoning’ the matrix of combinations according to its diagonals. The trial begins in zone Z₁ = {(A₁, B₁)}, and the first cohort of patients be enrolled on this ‘lowest’ combination. At the first observation of a toxicity in one of the patients, the first stage is closed, and the second (model-based) stage is opened. As long as no toxicities occur, cohorts of patients are examined at each dose within the currently occupied zone, before escalating to the next highest zone. If (A₁, B₁) was tried and deemed ‘safe’, the trial would escalate to zone Z₂ = {(A₁, B₂), (A₂, B₁)}, similar to CDP. If more than one dose is contained within a particular zone, we can sample without replacement from the doses available within the zone. Therefore, the next cohort is enrolled on a dose that is chosen randomly from (A₁, B₂) and (A₂, B₁). The trial is not allowed to advance to zone Z₃ in the first stage until a cohort of patients has been observed at both all combinations in Z₂. This procedure continues until a toxicity is observed, or all available zones have been exhausted.

Stage 2

Subsequent to a DLT being observed, the second stage of the trial begins.

1. Based on the accumulated data from i patients Ω_i, the estimated toxicity probabilities π̂_jk are obtained for all combinations being tested, based on the procedure described previously.

2. The next entered patient is then allocated to the dose combination with estimated toxicity probability closest to the target toxicity rate so that |π̂_jk − ϕ| is minimized.

3. There is no skipping restriction placed on escalation in the WCO method to allow for adequate exploration of the drug combination space.

4. For trials subject to partial orders, there may be more than one combination with DLT probability closest to the target. If there is a ‘tie’ between two or more combinations, the patient will be randomized to one of the combinations with DLT probability closest to the target. The trial stops once enough information accumulates about the MTD.

3. Simulation studies

3.1. Motivating examples

Our objective is to compare the five model-based dose-finding methods under the settings that we often encounter in practice. To accommodate this requirement, we describe examples used to illustrate the behavior of the competing methods in the simulation studies. Each of the motivating examples is at least partly based on combination studies that have been published [7] have recently been Food and Drug Administration (FDA)/Institutional Review Board (IRB) approved at an National Cancer Institute-designated cancer center or have involved initial study-planning discussions with clinicians for planning a study. Therefore, some of the dose-toxicity scenarios were taken from study protocols, so they are a representative of what was reviewed by the FDA and/or the IRB in approving the study. The simulation results will shed some light on comparative performance of competing methods in the event they had been used to design the motivating trials. It should be noted that each of these studies incorporated various stopping rules in order to terminate the trial once enough information about the MTD combination has been obtained, or in the presence of undesirable toxicity. It is very difficult to compare methods under various stopping criteria, so we chose to conduct our simulations using a fixed sample size, justification for which is given in each of the following examples.

Example 1

A single-arm, non-randomized, open-label dose escalation study was designed to determine the MTDC/appropriate phase II dose combination of two small molecule inhibitors (agents A and B) for refractory solid tumors and untreated metastatic disease. Agent A contained three doses (1.0, 1.5, and 2.0 mg/day), and agent B contained three doses (1000, 1250, and 1500 mg/day), for a total of nine (3 × 3) drug combinations. Dose escalation was to be conducted using the two-stage WCO [20] for dose finding with combinations of agents. Each stage treated patients in single patient cohorts, and the target DLT rate for determining the MTD combination was 30%. Because the design implemented a stopping rule, the sample size was estimated from the simulation results. Although the maximum accrual was set at 54 patients, on average across 1000 simulations, between approximately n = 22 and 32 patients were required to complete the study, with most sample sizes ranging from 28 to 32 patients.

Example 2

The study described in Gandhi et al. [7] is a phase I trial of neratinib in combination with temsirolimus in patients with human epidermal growth factor receptor 2-dependent and other solid tumors. Neratinib was given in four escalating doses (120, 160, 200, and 240 mg), and four doses of temsirolimus were also tested (15, 25, 50, and 75mg), for a total of 16 (4 × 4) drug combinations. Two MTD’s (200 mg neratinib/25 mg temsirolimus and 160 mg neratinib/50 mg temsirolimus) were found using a non-parametric up-and-down algorithmic-based sequential design [3]. Again, our objective in this current work is to examine the behavior of model-based designs that aim to identify a single MTD combination, but this example provides us with a relevant study on which to investigate performance. The MTD contour was defined by combinations that achieve a DLT rate closest to but below 33%, and the simulations studies in the supplementary material to Gandhi et al. [7] were based on a sample size of n = 32 patients for the design [3] and, on average, n = 18.8 patients for the 3 + 3 design. In keeping things consistent with other examples, we chose to evaluate performance of competing methods in choosing a single combination closest to a target DLT rate of 30%, based on a fixed sample size of n = 30 patients.

Example 3

An open-label, phase I trial is currently being designed at the University of Virginia Cancer Center. The trial will investigate the combination of two small molecule inhibitors (agents A and B) in patients with relapsed or refractory mantle cell lymphoma. The primary objective of the study is to determine the MTDC of two doses (200 and 400 mg) of agent A and four doses (140, 280, 420, and 560 mg) of agent B. The two-staged design of Wages et al. [20] will be used to estimate the MTDC of the eight (2 × 4) drug combination matrix. Each stage will treat participants in single-patient cohorts. The target DLT rate for determining the MTDC is 30%. A maximum sample size of n = 48 patients with a stopping rule and a fixed sample size of n = 30 patients were both investigated in the protocol development stage. Our simulation studies will investigate operating characteristics for n = 30 eligible patients.

Example 4

The final example is a revised version of example 1, in which two lower doses of agent B were added because of safety concerns. Agent A contained three doses (1.0, 1.5, and 2.0 mg/day), and agent B contained five doses (500, 750, 1000, 1250, and 1500 mg/day), for a total of 15 (3 × 5) drug combinations. The remainder of the information contained in example 1 holds for this example as well. This trial was FDA and IRB approved at the University of Virginia Cancer Center.

3.2. Simulation setting

3.2.1. Common settings

Motivated by the aforementioned examples, we compared the operating characteristics among the five methods by simulating 16 scenarios with 3 × 3, 4 × 4, 2 × 4, and 3 × 5 dose combination matrices with different positions and number of true MTDCs, as shown in Table II. The target toxicity probability that is clinically allowed, ϕ, is set to 0.3. For each simulated trial, no stopping rule was specified so as to exhaust the pre-specified maximum sample size N_max = 30. Each simulation study consisted of 1000 trials. The YYC and BW designs are based on Bayesian methods that require the proper elicitation of priors. We did our best to make the prior elicitations for these methods as comparable and as consistent as possible so as to not bias performance for a particular method.

Table II.

Sixteen scenarios for a two-agent combination trial (maximum tolerated dose (MTD) combinations are in boldface).

	A
		1	2	3	4	5	1	2	3	4	5
			Scenario 1					Scenario 2
	3	0.30	0.40	0.50			0.50	0.70	0.80
	2	0.20	0.30	0.40			0.30	0.60	0.70
	1	0.10	0.20	0.30			0.05	0.30	0.50
			Scenario 3					Scenario 4
	3	0.40	0.60	0.80			0.15	0.40	0.60
	2	0.30	0.50	0.70			0.05	0.30	0.40
	1	0.05	0.10	0.40			0.01	0.05	0.15
			Scenario 5					Scenario 6
	4	0.30	0.50	0.65	0.70		0.30	0.50	0.60	0.70
	3	0.10	0.30	0.60	0.65		0.15	0.40	0.50	0.60
	2	0.05	0.10	0.30	0.50		0.10	0.30	0.40	0.50
	1	0.01	0.05	0.10	0.30		0.05	0.10	0.15	0.30
			Scenario 7					Scenario 8
B	4	0.40	0.45	0.60	0.85		0.15	0.60	0.75	0.80
	3	0.15	0.30	0.55	0.60		0.10	0.45	0.70	0.75
	2	0.08	0.15	0.23	0.30		0.04	0.30	0.45	0.60
	1	0.01	0.02	0.03	0.04		0.02	0.10	0.15	0.40
			Scenario 9					Scenario 10
	2	0.10	0.20	0.30	0.40		0.30	0.40	0.50	0.60
	1	0.05	0.10	0.20	0.30		0.01	0.10	0.20	0.30
			Scenario 11					Scenario 12
	2	0.15	0.28	0.32	0.34		0.50	0.60	0.70	0.80
	1	0.10	0.15	0.28	0.32		0.10	0.20	0.30	0.40
			Scenario 13					Scenario 14
	3	0.25	0.25	0.40	0.50	0.70	0.20	0.45	0.50	0.60	0.75
	2	0.10	0.10	0.30	0.40	0.50	0.05	0.30	0.45	0.55	0.60
	1	0.05	0.05	0.25	0.30	0.40	0.01	0.05	0.15	0.30	0.50
			Scenario 15					Scenario 16
	3	0.30	0.35	0.40	0.45	0.60	0.10	0.20	0.40	0.55	0.65
	2	0.05	0.20	0.30	0.40	0.45	0.05	0.10	0.30	0.50	0.60
	1	0.01	0.05	0.10	0.20	0.30	0.01	0.05	0.10	0.20	0.40

3.2.2. Settings for YYC

We used the executable code released at http://odin.mdacc.tmc.edu/~yyuan/index_code.html to perform the YYC method. The software contains default priors for the parameters, which cannot be changed by the user. Therefore, we assumed gamma(2, 2) as the prior distribution for α and β and gamma(0.1, 0.1) as the prior distribution for γ. Motivated by the description in Section 2.1, the values of p_j are set to (0.15, 0.3) for J = 2, (0.1, 0.2, 0.3) for J = 3, (0.075, 0.15, 0.225, 0.3) for J = 4, and (0.06, 0.12, 0.18, 0.24, 0.30) for J = 5, respectively. The same setting are made for q_k. Each simulated trial used cohorts of size 3 to guide allocation. The fixed probability cut-offs for dose escalation and de-escalation are c_e = 0.80 and c_d = 0.45, respectively, which are also default values used by the software.

3.2.3. Settings for BW

We used the R code released at http://www-personal.umich.edu/~tombraun/BraunWang/ to perform the BW method. The variance parameter σ² is set to 3 in order to stabilize the implementation of the R package rjags. The BW method requires the investigator to have sufficient historical information regarding DLT probabilities of the doses of both agents, when combined with the lowest dose of the other agent. Because we are, in a sense, ‘retrospectively’ evaluating the performance of the BW method in designing the motivating examples, it is obviously impossible to utilize investigator information in prior elicitation. The prior probability of each dose combination is shown in Table III, in which it can be seen that a priori values p_j1 and q_1k are equal, or very close to, the a priori DLT rates for the YYC method. Each simulated trial used cohorts of size 1 to guide allocation.

3.2.4. Setting for HHM

We performed the HHM method using the SAS/IML in SAS 9.3 (SAS Institute Inc., Cary, NC, USA). Although we can set the actual or standardized dose levels for x₁ and x₂ in planning an actual trial, we set them arithmetically in this simulation as in Hirakawa et al. (2013) [21], x₁ = 1, 2, 3 and x₂ = 1, 2, 3 for 3 × 3 dose combinations, x₁ = 1, 2, 3, 4 and x₂ = 1, 2, 3, 4 for 4 × 4 dose combinations, x₁ = 1, 2 and x₂ = 1, 2, 3, 4 for 2 × 4 dose combinations, and x₁ = 1, 2, 3 and x₂ = 1, 2, 3, 4, 5 for 3 × 5 dose combinations. Given the dose levels for x₁ and x₂, we fine-tuned the value of the fixed intercept β₀ in a preliminary simulation experiment and set it to −3. Thus, we recommend to fine-tune β₀ for the values of the dose levels we determined. Finally, c₁ and c₂ are commonly set to 0.05. Each simulated trial used cohorts of size 3 to guide allocation.

3.2.5. Setting for CDP

For CDP, we present results for a prior that set the prior mean equal to the target DLT rate and utilize a constant value across all combinations for the prior upper 95% limit. As in Conaway et al. [14], we take the prior mean to equal 0.30 and a prior upper 95% limit of 0.70 for all combinations. We utilized eight possible orderings in scenarios 1–8 and 13–16 and five possible orderings in scenarios 9–12. Both stages used cohorts of size 1.

3.2.6. Setting for WCO

We utilized the same set of possible orderings as CDP. A uniform prior, τ, was placed on the orderings. The skeleton values, p_jk(m), were generated according to the algorithm of Lee and Cheung [33] using the getprior function in Rpackage dfcrm. Specifically, for 3×3 combinations, we used getprior(0.05,0.30,4,9); for 4×4 combinations, we used getprior(0.05,0.30,7,16); for 2×4 combinations, we used getprior(0.05,0.30,4,8); and for 3 × 5 combinations, we used getprior(0.05,0.30,7,15). All simulation results were carried out using the functions of pocrm with a cohort size of 1 in both stages.

3.3. Simulation results

3.3.1. Notable operating characteristics

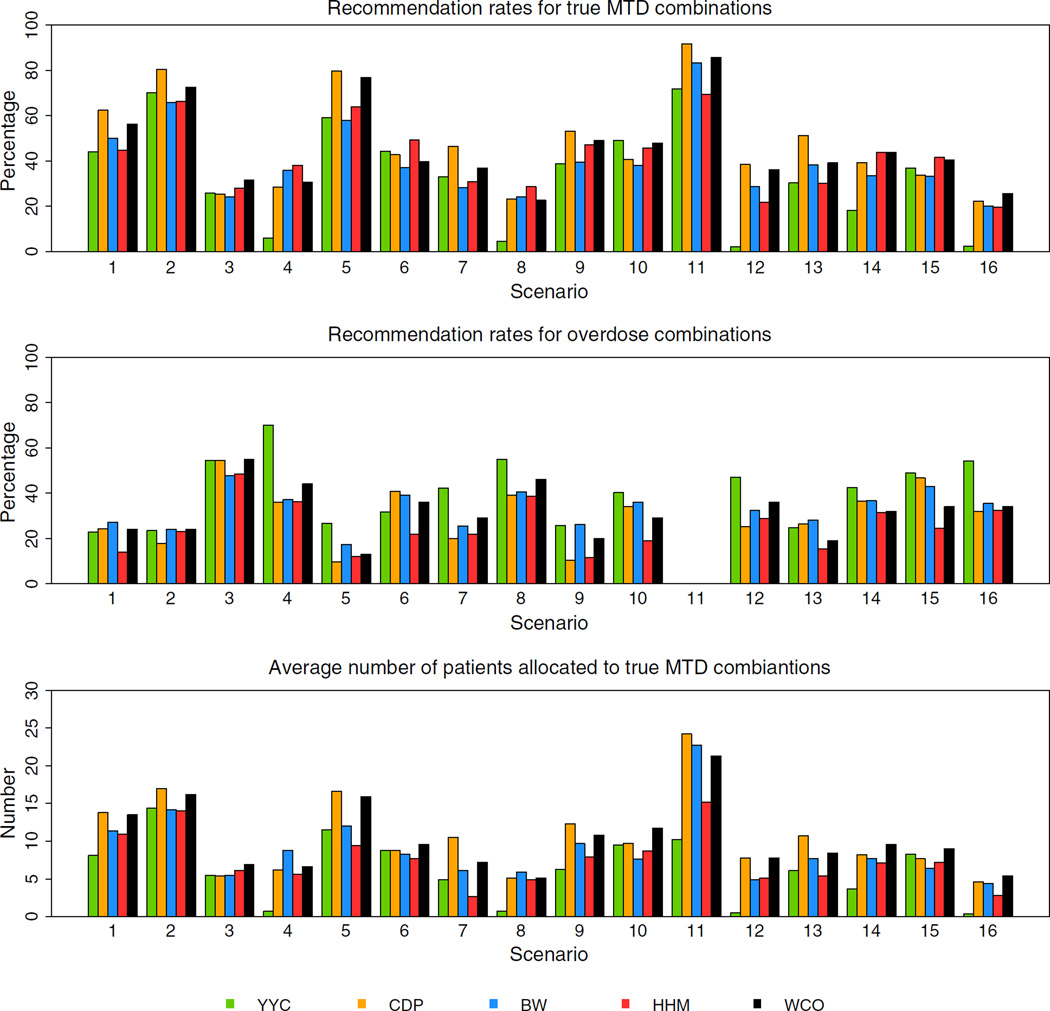
Figures 1 and 2 show the operating characteristics of the five methods under 16 scenarios. Table summaries of these figures can be found in the supporting web materials. For scenarios 1 and 2, the CDP and WCO methods showed higher recommendation rates for true MTDCs than the YYC, BW, and HHM methods by 7–15%, while those were comparable among the YYC, BW, and HHM methods. The CDP and WCO methods also allocated, on average, more patients to true MTDCs. The recommendation rates for true MTDCs were similar among all the methods under scenario 3, with the WCO method being slightly higher than the other methods, while allocating the most patients on average to the MTDCs. The recommendation rates of the BW and HHM methods were higher than the other three methods under scenario 4, yet the BW allocated the most patients on average to the true MTDCs. The recommendation rates for the ODCs of the HHM and CDP methods were slightly lower than those of the BW and WCO methods in this scenario. In terms of recommending true MTDCs, similar relationships were observed between scenarios 1 and 5 and between scenarios 4 and 8, respectively. The HHM method outperformed the other four methods in scenario 6, although the other four methods allocated more patients on average to MTDCs. The CDP method outperformed the other methods in scenario 7 while also treating the most patients at MTDCs. The recommendation rates for true MTDCs of the CDP, HHM, and WCO methods in scenario 9, of the YYC, HHM, and WCO methods in scenario 10, of the CDP, BW, and WCO methods in scenario 11, and of the CDP and WCO methods in scenario 12 were higher than the remaining methods, respectively. The difference of the recommendation rates between the methods was approximately 5–15%. The average number of patients allocated to true MTDCs of the CDP method in scenario 9, of the WCO method in scenario 10, of the CDP, BW, and WCO methods in scenario 11, and of the CDP and WCO methods in scenario 12 were higher than the other methods, respectively. The CDP or WCO method performed better than or as well as the other three methods under scenarios 9–12, and a similar tendency was observed under scenarios 13–16. The HHM method was competitive of the WCO method in scenarios 14 and 15. In terms of recommending the ODCs, the CDP method was lowest among the five methods under scenarios 9 an 12, while HHM was lowest among the methods in scenarios 10 and 13–16.

Figure 1.

Summary of the operating characteristics of the five methods in all scenarios. MTD, maximum tolerated dose.

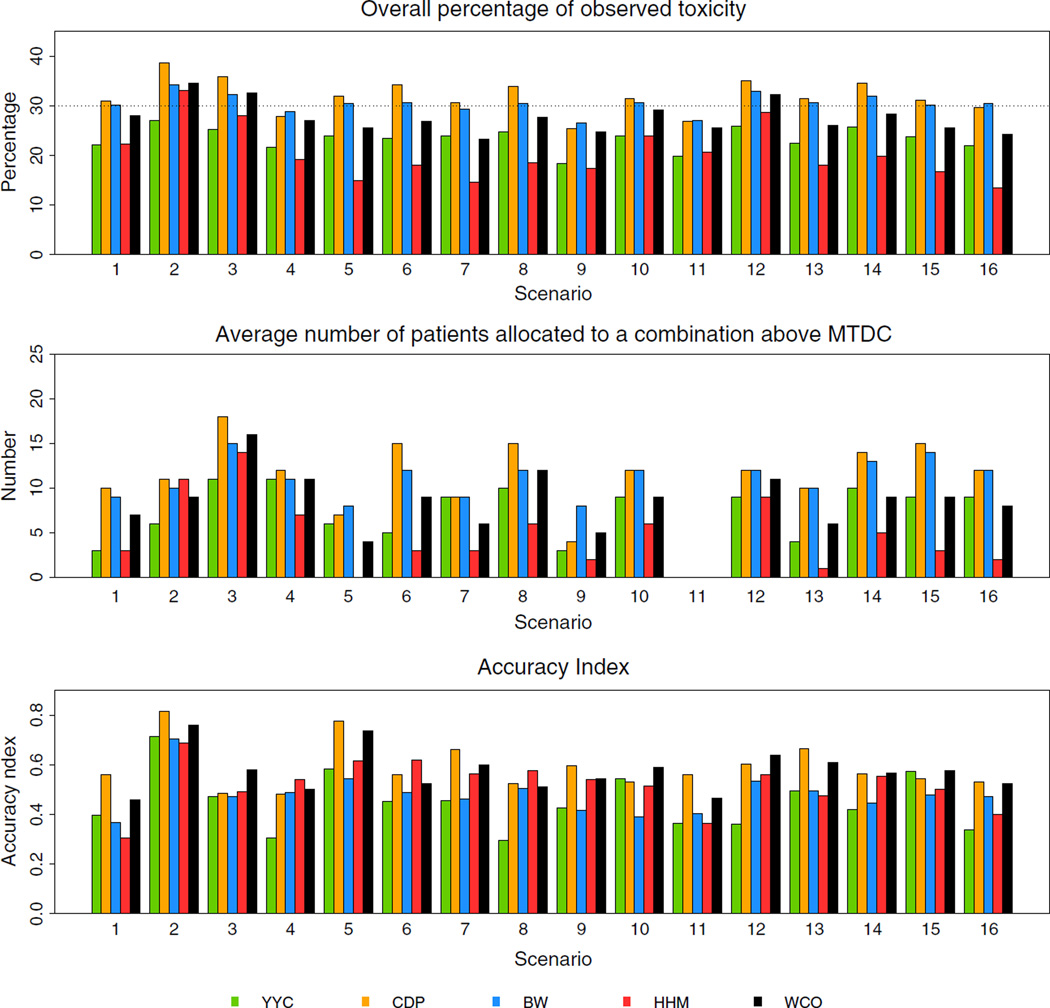
Figure 2.

Summary of the operating characteristics of the five methods in all scenarios. MTDC, maximum tolerated dose combination.

3.3.2. Average performance

Across the 16 scenarios, the YYC, CDP, BW, WCO, and HHM methods demonstrated averages 34%, 47%, 40%, 46%, and 42% recommendation rates for true MTDCs, respectively. The YYC, CDP, BW, WCO, and HHM methods demonstrated averages 41%, 30%, 33%, 32%, and 25% recommendation rates for ODCs, respectively. The average number of patients allocated to true MTDCs of the YYC, CDP, BW, WCO, and HHM methods were averages of 6, 11, 9, 10, and 8, respectively. The overall percentage of observed toxicities of the YYC, CDP, BW, WCO, and HHM methods were averages of 23%, 32%, 30%, 28%, and 20%, respectively. Average number of patients allocated to at a dose combination above the true MTDCs of the YYC, CDP, BW, WCO, and HHM methods were averages of 8, 12, 11, 9, and 5, respectively. In considering a benchmark for this summary measure, Cheung [36] considers the ideal situation in which all patients are treated at the true MTDC. In this case, we would expect a ϕ = 30% observed toxicity rate. Therefore, a design that results in roughly ϕ% toxicities on average per trial can be considered safe. The CDP, BW, and WCO methods yield the best performance with respect to an observed toxicity rate closest to the target toxicity rate. Cheung [36] also considers that the recommendation rates for true MTDCs are the most immediate index for accuracy, which can be used to compare different methods, while the entire distribution of selected dose combination does provide more detailed information than what the recommendation rates for true MTDCs alone suggests. Cheung [36] proposes to use the accuracy index, after n patients, defined as

$$A_n=1-J\times K\times \frac{\sum _{j=1}^J\sum _{k=1}^K|{\pi }_{jk}-\varphi |\times {\rho }_{jk}}{\sum _{j=1}^J\sum _{k=1}^K|{\pi }_{jk}-\varphi |},$$

where π_jk is the true toxicity probability of dose combination (A_j, B_k) and ρ_jk is the probability of selecting dose combination (A_j, B_k). A large index indicates high accuracy, and the maximum value of the index is 1. Based on the accuracy index, the CDP methods showed the maximum value of 0.59, and the WCO method showed the second largest value of 0.57.

3.3.3. Operating characteristics for each representative setting

According to the results of simulation studies, we found that the operating characteristics of the dose-finding method varied depending on (1) whether the dose combination matrix is square or not; (2) whether the true MTDCs exist within the same group consisting of the diagonals of the dose combination matrix; and (3) the number of true MTDCs. Table IV shows the average recommendation rates for true MTDCs and ODCs of the five methods with respect to each type of the dose combination matrix, and position and number of true MTDCs. In the cases of the square dose-combination matrix, the CDP method outperformed the YYC, BW, and HHM methods and was competitive with the WCO method when the true MTDCs exist along with the diagonals of the dose-combination matrix and the number of true MTDCs is more than or equal to 2, conclusions that held true for patient allocation as well. The CDP method provided a recommendation rate that was slightly better than the other four methods when the true MTDCs do not exist along with the diagonals of the dose-combination matrix but the number of true MTDCs is more than or equal to 2. CDP method also allocated the highest number of patients to true MTDCs on average. The HHM methods demonstrated the highest recommendation rates for true MTDCs when the number of true MTDCs is one, while the CDP and BW methods allocated the most patients to true MTDCs. Next, in the cases of the rectangle dose combination matrix, the CDP method outperformed the other four methods when the true MTDCs exist along with the diagonals of the dose-combination matrix and the number of true MTDCs is more than or equal to 2. CDP and WCO outperform the other three methods when the number of true MTDCs is one, while the HHM and WCO methods did when the true MTDCs do not exist along with the diagonals of the dose-combination matrix but the number of true MTDCs is more than or equal to 2. In all three of these situations, either the WCO or the CDP allocated the most patients on average to true MTDCs. In terms of recommending the ODCs, the HHM method was superior to the other four methods when the true MTDCs exist along with the diagonals of the dose-combination matrix and the number of true MTDCs is more than or equal to 2. HHM demonstrated the lowest recommendation rates for the ODCs under most of the other configurations presented. The HHM method can be considered a more conservative method than the others evaluated in this work. While it recommends ODCs less than the other methods in most scenarios presented, it also demonstrates one of the lower numbers in terms of average patients allocated to true MTDCs, and it yields the lowest (and furthest from 30%) observed toxicity rate among the methods considered. When this information is combined, it can be concluded that HHM tends to recommend combinations and treat more patients at combinations below the true MTDC than the other methods.

Table IV.

The recommendation rates for true maximum tolerated dose combinations (MTDCs) and over-dose combinations (ODCs) on average with respect to each type of the dose combination matrix, and position and number of true MTDCs. (The percentages for the best method are in bold).

			Rec % for true MTDCs					Rec % for ODCs
Dose combination matrix	Position and number of true MTDCs	Scenario	YYC	CDP	BW	WCO	HHM	YYC	CDP	BW	WCO	HHM
Square (i.e., 3 × 3 and 4 × 4)	Diagonal and ⩾2 true MTDCs	1, 2, 5	58	74	58	69	58	24	17	23	20	16
	Non-diagonal and ⩾2 true MTDCs	6, 7	39	45	33	38	40	37	38	33	33	22
	1 true MTDC	3, 4, 8	12	26	28	28	32	60	37	42	48	39
Rectangle (i.e., 2 × 4 and 3 × 5)	Diagonal and ⩾2 true MTDCs	9, 13	35	52	39	44	39	25	28	27	19	14
	Non-diagonal and ⩾2 true MTDCs	10, 14, 15	35	39	38	44	44	44	20	40	32	25
	1 true MTDC	12, 16	2	25	30	31	21	51	32	34	35	31
			Avg allocation to true MTDCs (#)					Accuracy index
Square (i.e., 3 × 3 and 4 × 4)	Diagonal and ⩾2 true MTDCs	1, 2, 5	11	16	13	15	11	0.57	0.72	0.54	0.65	0.54
	Non-diagonal and ⩾2 true MTDCs	6, 7	10	7	7	8	5	0.36	0.62	0.49	0.53	0.54
	1 true MTDC	3, 4, 8	2	7	7	6	6	0.45	0.54	0.48	0.56	0.59
Rectangle (i.e., 2 × 4 and 3 × 5)	Diagonal and ⩾2 true MTDCs	9, 13	6	9	9	10	7	0.46	0.60	0.46	0.58	0.51
	Non-diagonal and ⩾2 true MTDCs	10, 14, 15	7	13	7	10	8	0.51	0.64	0.44	0.58	0.52
	1 true MTDC	12, 16	1	10	5	7	4	0.35	0.59	0.51	0.58	0.48

3.4. Some possible rationales for the observed performance difference

The method in group (1) (i.e., YYC, BW, and HHM) showed the best performance with respect to recommendation for true MTDC(s) under five scenarios, while that in group (2) (i.e., CDP and WCO) did under 10 scenarios. In scenario 14, the WCO and HHM methods yielded nearly identical performance. Accordingly, the underparameterized approaches may be more efficient than the approaches using flexible model with several parameters. This is because that parameter estimation generally does not work well under the practical sample size of 30, irrespective of whether frequentist and Bayesian approaches are employed. Additionally, the cohort size of trial may also impact on the difference between the methods in groups (1) and (2). To further examine this, we ran YYC using cohorts of size 1, but the results were very similar on average. There were differences within particular scenarios, with size 3 doing better in some cases and size 1 doing better in others. For instance, in scenario 8, YYC with size 3 yielded a recommendation percentage for true MTDC’s of 4.6%. Using cohorts of size 1 increased this to 8.4%. Conversely, decreasing the cohort size from 3 to 1 decreased the recommendation percentage in scenario 6 from 44.3% to 38.4%. The average recommendation percentage for true MTDC across the 16 scenarios was 34% for size 3 and 35% for size 1.We also ran HHM using cohorts of size 1 and found that the average recommendation percentage for true MTDC across the 16 scenarios was 40% for size 1 and slightly smaller than that for size 3 (i.e., 42%). In the CDP and WCO methods using cohort size of 1, once a DLT being observed in stage 1, they can quickly move to stage 2 and obtain model-based estimates. This is a very attractive feature for model-based dose-finding methods. Although the restrictions on skipping dose levels between CDP and WCO are quite different, we could not observe its impact on the operating characteristics using the six evaluation indices. Among the methods in group (1), the superiority in terms of recommending true MTDC(s) were HHM, BW, and YYC in that order. The shrinkage logistic model includes the model parameters for agents A and B and its interaction but does not need to specify the prior toxicity probability for each agent and hyperparameter for prior distribution as in YYC and BW. Furthermore, YYC and BW commonly specify the prior toxicity probability for each agent, but the number of hyperparameters for the prior distributions in BW (e.g., only σ²) is smaller than that of YYC (e.g., α, β, and γ). Similar results were observed in the accuracy index. Thus, our simulation studies suggested that the degree of assumption with regard to prior toxicity probability, hyperparameters, and dose-toxicity model in the method may be associated with the average performances of selecting true MTDCs.

4. Discussions and conclusions

In this study, we revealed the operating characteristics of the model-based dose-finding methods using the practical sample size of 30 under the various toxicity scenarios, motivated by real phase I trial settings. Although there are certain scenarios in which each of the methods performs well and operating characteristics between methods are comparable, on average, the CDP (47%) and WCO (46%) methods yield the largest recommendation rates for true MTDC’s by at least 4% over the nearest competitor (HHM, 42%). These conclusions hold for patient allocation to true MTDC’s as well. This average performance is across 16 scenarios that encompass a wide variety of practical situations (i.e., dimension of combination matrix, location and number of true MTDC’s, etc.). In the supporting web materials, we considered additional scenarios in which there was no ‘perfect’ MTDC. That is, in each scenario, there are no combinations with true DLT rate exactly equal to the target. In these scenarios, we evaluated performance of each method in choosing, as the MTDC, combinations that have true DLT rates close to the target rate. The conclusions from the simulation studies above held, with CDP yielding the highest (38.3%) average recommendation percentage for combinations within 5% of the target rate and WCO with the second highest (37.1%).

The simulations studies indicated that the performances in terms of recommending true MTDCs among the five methods may be associated with the degree of assumption required in each method. Specifically, the uncertain assumptions (e.g., prior toxicity probability, hyperparameters, and specific dose-toxicity model) are less in order of CDP, WCO, HHM, BW, and YYC, and the performances in terms of recommending true MTDCs were on average better in this order. This tendency was also found in the accuracy index. Although the operating characteristic of a dose-finding method is influenced by many methodological characteristics, this hypothetical consideration would be one of the reasons for the performance differences among the five methods.

Within the context of the motivating examples shown in Section 3.1, it is important to consider what methods appear to be most appropriate for each example in terms of selecting true MTDCs. For example 1 with a 3 × 3 dose combination matrix, CDP would be favorable if we expect ⩾2 true MTDCs, while HHM may be favorable if we expect 1 true MTDC. In example 2, the two diagonal MTDCs have been identified among 4 × 4 dose combination matrix; therefore, CDP would be most appropriate in this setting if that is true. For examples 3 and 4 with rectangular dose combination matrix, the methods of group (2) (i.e., CDP and WCO) would be suitable irrespective of the position and number of true MTDCs.

Based on the results of simulation studies, we provide some recommendations in implementing each method in practice. The YYC and BW methods require the specifications for both the toxicity probabilities of two agents and hyperparameters of prior distributions; therefore, these methods would be most useful in the cases where the toxicity data are available from a previous phase I monotherapy trial for each agent. We need to pay particular attention to use the YYC method because its operating characteristics were greatly impacted by the toxicity scenarios. The performance of the BW method was intermediate between the HHM and YYC methods. In implementing BW, the prior value of σ² should be fine-tuned, as the authors recommend. The HHM method can be employed without prior information on the two agents but requires the MLE for the three parameters in the shrinkage logistic model; therefore, the majority of the planned sample size enrolled into the stage of start-up rule, resulting in reduced recommendation rate for true MTDCs. If investigators desire to be a bit more conservative while still maintaining an adequate recommendation rate for true MTDCs, the HHM method can be recommended.

The CDP and WCO methods would be most useful in the practical setting of ordinary phase I combination trials because the prior considerations compared to those required by YYC and BW are considerably less. The escalation algorithm of CDP is complex and can be difficult and time-consuming to program. Conversely, the WCO method builds off of the well-known CRM and is likely to be more easily understood by clinicians and review boards. YYC, BW, and WCO all have available software on the web that can be used for simulating design-operating characteristics, whereas BW and WCO are the only methods of those studied that have available software for design implementation (i.e., obtaining a combination recommendation for the next entered cohort, given the data to that point in the trial).