Fig. 1.
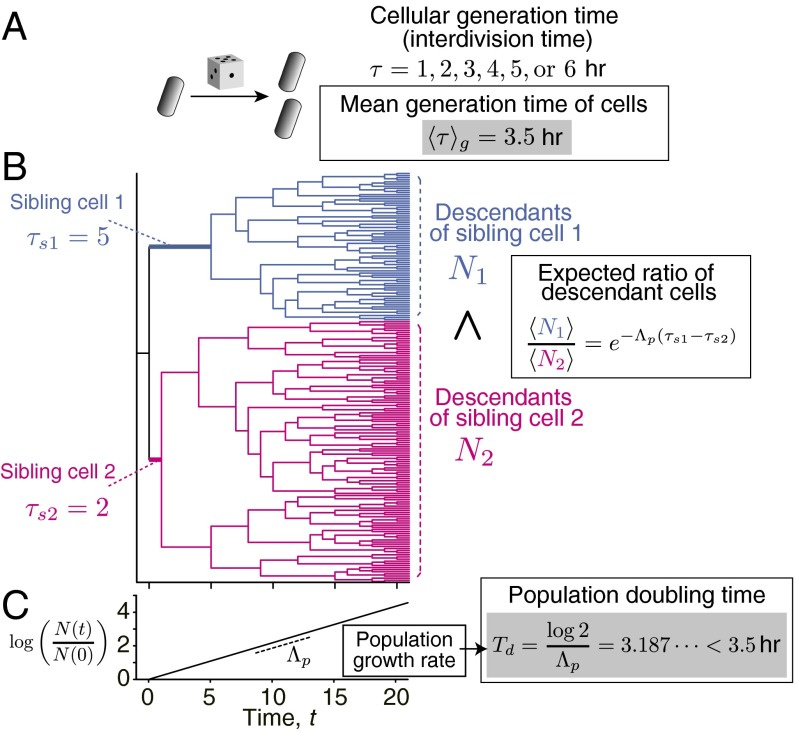
Competition within a population caused by growth noise and its consequence to population growth rate. (A) Toy model of cell proliferation. Here, we consider a model of cell proliferation in which all of the cells in a population determine their generation time (interdivision time) randomly by throwing a dice to learn the consequences of intrapopulation growth noise. In this setting, cells can take either of the six possible choices of generation time, h, with the equal probability of 1/6. The mean generation time is thus = 3.5 h. (B) Example of pedigree tree showing competition between sibling cells. In this tree, two sibling cells were born from the common mother cell at t = 0 h, and divided with different generation times (sibling cell 1: τs1 = 5 h; and sibling cell 2: τs2 = 2 h). The descendant cells from the both sibling cells follow the same rule of cell divisions irrespectively of the ancestral generation time. The difference of generation time between the sibling cells 1 and 2 was caused just by chance, but the expected number of descendant cells becomes larger for the fast dividing sibling cell. The ratio of the expected number of descendant cells from those sibling cells at a certain future time point is , where Λp is the population growth rate. (C) Growth of cell population. When all of the cells in the population follow the same division rule in A, the number of cells in the population grows exponentially. The rate of this exponential growth is the “population growth rate,” Λp. The time required for the population to double the number of cells is the “population doubling time,” Td, i.e., . Therefore, Td = ln2/Λp. An interesting consequence of stochasticity in generation time is that population doubling time becomes smaller than the mean generation time, i.e., Td <. In the case of the dice population, Td = 3.187 h, which is indeed smaller than = 3.5 h.