Skip to main content
. Author manuscript; available in PMC: 2017 Feb 1.
Published in final edited form as: IEEE Trans Robot. 2015 Dec 17;32(1):20–35. doi: 10.1109/TRO.2015.2500422

Fig. 1.

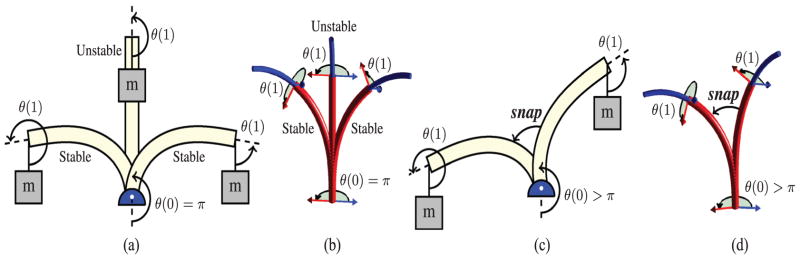
Fig. 1

The analogy between an Euler beam and a two-tube concentric tube robot for λ greater than its critical value. For the beam, θ (s) denotes the angle of the beam, while for the robot it denotes the angle between precurvature vectors. (a) There are three solutions when the base has been rotated to θ (0) = π. The straight solution is unstable and the two buckled solutions are stable. (b) When the tube precurvatures are anti-aligned at the base there exists one torsionless unstable solution and two stable buckled solutions. (c) As the base angle approaches some value θ (0) > π, the beam snaps into a new, stable configuration. (d) As the relative angle between the tubes approaches some value θ (0) > π the tubes snap into a new, stable configuration. Note that the value of θ (0) when the snap occurs depends on λ.