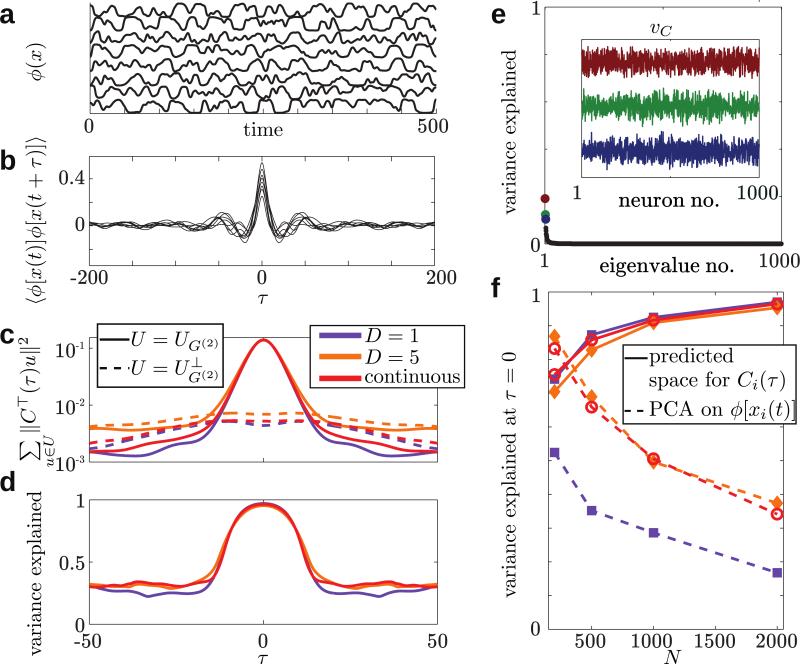
FIG. 2.

Low-dimensional structure of network dynamics. Traces of the firing rates ϕ[x_i(t)] (a) and autocorrelations C_i(τ) (b) of eight example neurons chosen at random from the network with continuous gain modulation (shown in the bottom row of Fig. 1). (c) The sum of squared projections of the vector C_i(τ) on the vectors spanning U_G⁽²⁾ (the active modes, solid lines) or $U_{G^{\left(2\right)}}^{\perp }$ (the inactive modes, dashed lines). The dimension of the subspace U_G⁽²⁾ is K★ = 1 for the network with g = const and K★ = 3 for the block and continuous cases (orange and red, respectively), much smaller than N – K★ ≈ N, orthogonal the dimension of the complement space $U_{G^{\left(2\right)}}^{\perp }$. (d) Our analytically derived subspace accounts for almost 100 percent of the variance in the autocorrelation vector for $\mid \tau \mid \lesssim 10$ (in units of the synaptic time constant). (e) Reducing the dimensionality of the dynamics via principal component analysis on ϕ(x) leads to vectors (inset) that account for a much smaller portion of the variance (when using same dimension K★ for the subspace), and lack structure that could be related to the connectivity. (f) Summary data from 50 simulated networks per parameter set (N, structure type) at τ = 0. As N grows the leak into $U_{G^{\left(2\right)}}^{\perp }$ diminishes if one reduces the space of the C_i(τ) data while the fraction of variance explained becomes smaller when using PCA on the ϕ[x_i(t)] data, a signature of the extensiveness of the dimension of the chaotic attractor.