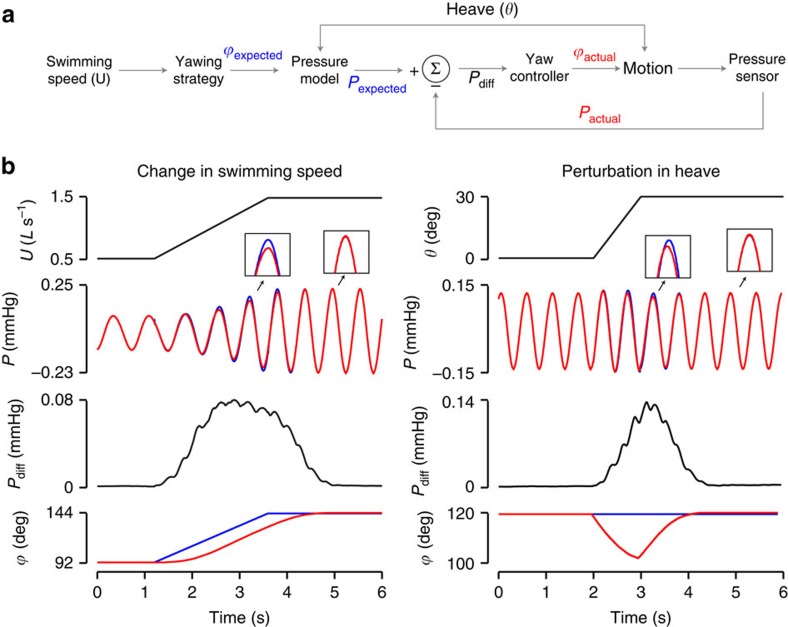
Figure 4. Proposed control architecture that universally regulates head movements of undulatory animals and machines in dynamic situations.

(a) Model to control head movements in order to operate at optimal phase angles during steady swimming. (b) A demonstration of this control architecture is seen for two simulations of natural behaviours: (i) a change in swimming speed (left column) and (ii) a perturbation in heave motion (right column). When fishes change their swimming speed or are exposed to a lateral perturbation, a difference between the expected (from experience) and measured pressure (lateral line sensing) is established. A gradient descent algorithm uses the pressure difference to adjust the phase angle iteratively. As phase angle approaches the target value, the pressure difference, and hence phase adjustments, decreases. This process repeats until the phase angle matches the target value. In both cases, a discrepancy between the desired and actual pressure initiates a corrective response in head movements in order to reach a stable behaviour. U, swimming speed; θ, phase angle of heave; ϕ, phase difference between yaw and heave; P, pressure; P_diff, pressure difference.