Figure 5.

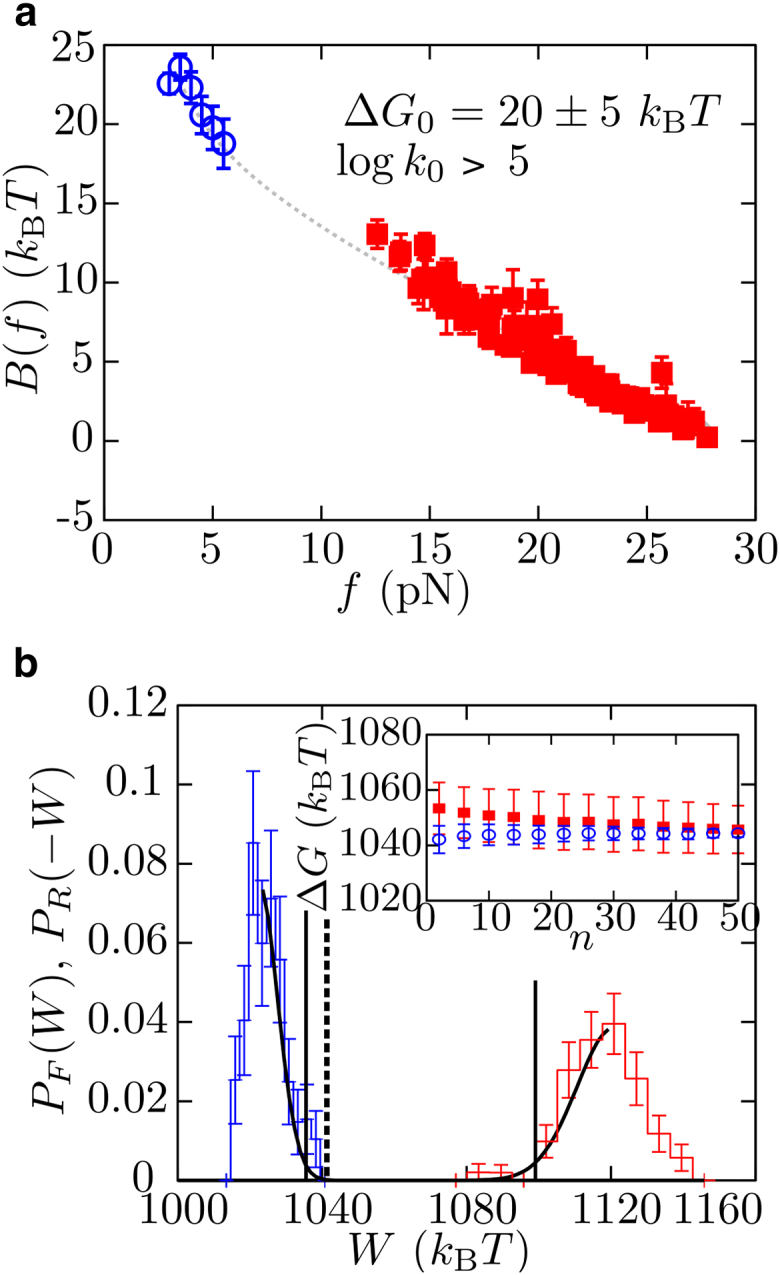
Reconstruction of the kinetic barrier and free-energy recovery of barnase. (a) Profile of the kinetic barrier B(f) determined using the CEBA method. (Red squares are obtained from logk_F→U(f) (Eq. S14a), and blue squares are obtained from logk_F←U(f) (Eq. S14c).) By imposing the continuity of B(f) from extrapolation (gray-dashed curve), we estimate the free energy of formation of barnase, ΔG₀ = 20 ± 5 k_BT. Additionally, assuming that at large forces the kinetic barrier goes to zero, gives a lower bound for logk₀ ∼ 5 (hence, k₀ ∼ 150 s⁻¹). Error bars are computed using the bootstrap method and by propagation of the errors of the elastic parameters. (b) Stretching (red) and releasing (blue) work histograms, and results of the fit to Eq. S18 of the respective leftmost tails (black). Error bars are obtained using the bootstrap method. (Solid vertical lines) Free energy values obtained using the Jarzynski estimator with stretching and releasing work values independently. (Dashed vertical line) Free energy estimation obtained by correcting the effect of bias using the random energy model. (Inset) Convergence of the Jarzynski estimated corrected by the bias using the random energy model as a function with the number of work measurements n. To see this figure in color, go online.