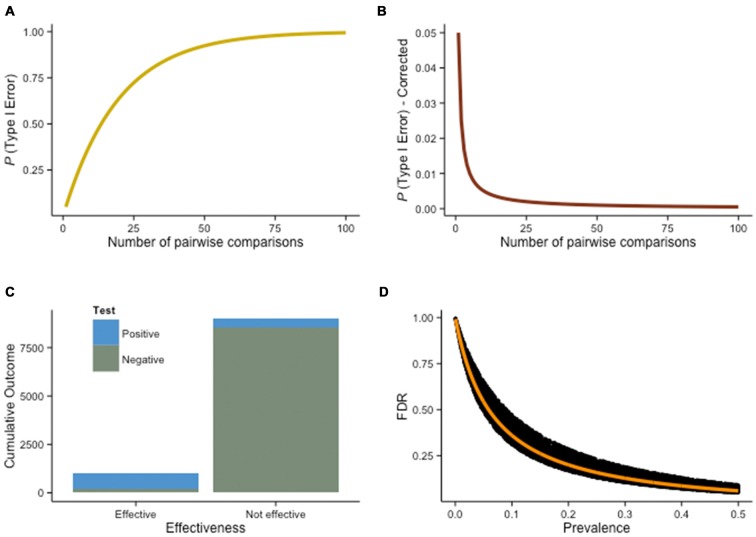
Figure 6.

Multiple comparisons problem. (A) True probability of a Type I error as a function of the number of pairwise comparisons (holding α = .05 constant for any given comparison). (B) A possible solution to the multiple comparisons problem is the Bonferroni correction, a rather conservative procedure—the false discovery rate (FDR) decreases, but so does the true discovery rate, increasing the chance to miss a true difference (β). (C) Assuming 10% of training interventions are truly effective (N = 10, 000), with power = .80 and α = .05, 450 interventions will yield false positives, while 800 will result in true positives. The FDR in this situation is 36% (more than a third of the positive results are not real), despite high power and standard α criteria. Therefore, this estimate is conservative—assuming 10% of the interventions are effective and 1−β = .80 is rather optimistic. (D) As the prevalence of an effect increases (e.g., higher percentage of effective interventions overall), the FDR decreases. This effect is illustrated here with a Monte Carlo simulation of the FDR as a function of prevalence, given 1−β free to vary such that .50 ≤ 1−β ≤ 1 (the orange line shows FDR when 1−β = .80).