Skip to main content
PMC home page
Nature Communications logoLink to Nature Communications
. 2016 Apr 12;7:11061. doi: 10.1038/ncomms11061

Dynamic information routing in complex networks

Christoph Kirst 1,2,3,4,5,a, Marc Timme 1,3,4, Demian Battaglia 6
PMCID: PMC4832059  PMID: 27067257

Abstract

Flexible information routing fundamentally underlies the function of many biological and artificial networks. Yet, how such systems may specifically communicate and dynamically route information is not well understood. Here we identify a generic mechanism to route information on top of collective dynamical reference states in complex networks. Switching between collective dynamics induces flexible reorganization of information sharing and routing patterns, as quantified by delayed mutual information and transfer entropy measures between activities of a network's units. We demonstrate the power of this mechanism specifically for oscillatory dynamics and analyse how individual unit properties, the network topology and external inputs co-act to systematically organize information routing. For multi-scale, modular architectures, we resolve routing patterns at all levels. Interestingly, local interventions within one sub-network may remotely determine nonlocal network-wide communication. These results help understanding and designing information routing patterns across systems where collective dynamics co-occurs with a communication function.

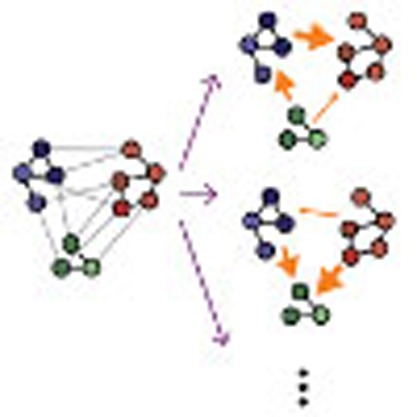Inline graphicFlexible information routing underlies the function of many biological and artificial networks. Here, the authors present a theoretical framework that shows how information can be flexibly routed across networks using collective reference dynamics and how local changes may induce remote rerouting.

Attuned function of many biological or technological networks relies on the precise yet dynamic communication between their subsystems. For instance, the behaviour of cells depends on the coordinated information transfer within gene-regulatory networks1,2 and flexible integration of information is conveyed by the activity of several neural populations during brain function3. Identifying general mechanisms for the routing of information across complex networks thus constitutes a key theoretical challenge with applications across fields, from systems biology to the engineering of smart distributed technology4,5,6.

Complex systems with a communication function often show characteristic dynamics, such as oscillatory or synchronous collective dynamics with a stochastic component7,8,9,10,11. Information is carried in the presence of these dynamics within and between neural circuits12,13, living cells14,15, ecological or social groups16,17 as well as technical communication systems, such as ad hoc sensor networks18,19. While such dynamics could simply reflect the properties of the interacting unit's, emergent collective dynamical states in biological networks can actually contribute to the system's function. For example, it has been hypothesized that the widely observed oscillatory phenomena in biological networks enable emergent and flexible information routing12. Yet, what are the precise mechanism by which collective dynamics contribute to organizing communication in networks? Moreover, how do the intrinsic dynamics of units, their interaction topology and function as well as external driving signals and noise create specific patterns of information routing?

In this article, we derive a theory for information routing in complex networked systems, revealing the joint impact of all these elements. We identify a generic mechanism to dynamically route information in complex networked systems by conveying information in fluctuations around a collective dynamical reference state. Propagation of information then depends on the underlying reference dynamics and switching between multiple stable states induces flexible rerouting of information, even if the physical network stays unchanged. For oscillatory dynamics, analytic predictions show precisely how the physical coupling structure, the units' properties and the dynamical state of the network co-act to generate a specific communication pattern, quantified by time-delayed mutual information (dMI)20,21 and transfer entropy22 curves between time-series of the network's units. Resorting to a collective phase description23, our theory further resolves communication patterns at all levels of multi-scale, modular topologies24,25, as ubiquitous, for example, in the brain connectome and biochemical regulatory networks26,27,28,29. Interestingly, local interventions within one sub-network may remotely modify information transfer between other seemingly unrelated sub-networks. Finally, a combinatorial number of information routing patterns (IRPs) emerge if several multi-stable subsystems are combined into a larger modular network. These relations between multi-scale connectivity, collective network dynamics and flexible information routing have potential applications in the reconstruction and design of gene-regulatory circuits15,30, wireless communication networks4,19 or to the analysis of cognitive functions31,32,33,34,35, among others. Moreover, these results offer generic insights into mechanisms for flexible and self-organized information routing in complex networked systems.

Results

Information routing via collective dynamics

To better understand how collective dynamics may contribute to specifically distribute bits of information from external or locally computed signals through a network or to it s downstream components we first consider a generic stochastic dynamical system. It evolves in time t according to

graphic file with name ncomms11061-m1.jpg

where x=(x1,…, xN) denotes the variables of the network nodes, f describes the intrinsic dynamics of the network. The key premise is that the information to be routed through the network is carried in the stochastic external input ξ=(ξ1,…,ξN) driving instantaneous state variable fluctuations. To access the role of collective dynamics in routing this information we consider a deterministic intrinsic reference state x(ref) (t) solving (2) in the absence of signals (ξ=0).

We use information theoretic measures that quantify the amount of information shared and transferred between nodes, independent of how this information is encoded or decoded. More precisely, we measure information sharing between signal xi(t) and the time d lagged signal xj(t+d) of nodes i and j in the network via the time-delayed mutual information (dMI)20,21

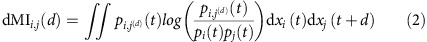graphic file with name ncomms11061-m2.jpg

Here pi(t) is the probability distribution of the variable xi(t) of unit i at time t and pi,j(d)(t) the joint distribution of xi(t) and the variable xj(t+d) lagged by d. As a second measure, we use the delayed transfer entropy (dTE)22 (cf. Methods) that genuinely measures information transfer between pairs of units36. Asymmetries in the curves dMIi,j(d) and dTEi→j(d) then indicate the dominant direction in which information is shared or transferred between nodes (cf. Supplementary Note 1).

To identify the role of the underlying reference dynamical state x(ref)(t) for network communication a small-noise expansion in the signals ξ turns a out to be ideally suited: while this expansion limits the analysis to the vicinity of a specific reference state which is usually regarded as a weakness of this technique, in the context of our study, this property is highly advantageous as it directly conditions the calculations on a particular dynamical state and enables us to extract it s role for the emergent pattern of information routing within the network. For white noise sources ξ this method yields general expressions for the conditional probabilities p(x(t+d)|x(t)) that depend on x(ref)(t). Using this result the expressions for the dMI (2) and dTE (7) dMIi,j(d) and dTEi→j(d) become a function of the underlying collective reference dynamical state (cf. Methods and Supplementary Note 2). The dependency on this reference state then provides a generic mechanism to change communication in networks by manipulation the underlying collective dynamics. In the following we show how this general principle gives rise to a variety of mechanisms to flexibly change information routing in networks. We focus on oscillatory phenomena widely observed in networks with a communication function32,34,35,37,38.

Information exchange in phase signals

Oscillatory synchronization and phase locking8,10 provide a natural way for the temporal coordination between communicating units. Key variables in oscillator systems are the phases φi(t) at time t of the individual units i. In fact, a wide range of oscillating systems display similar phase dynamics8,11 (cf. Supplementary Note 3) and phase-based encoding schemes are common, for example, in the brain32,34,35, genetic circuits37 and artificial systems38.

We first focus on systems in a stationary state with a stationary distribution for which the expressions for the dMI and dTE become independent of the starting time t and only depend on the lag d and reference state φ(ref)(t). To assess the dominant direction of the shared information between two nodes, we quantify asymmetries in the dMI curve by using the difference δMIi,j=MIi→j−MIj→j between the integrated mutual informations 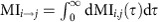Inline graphic and MIj→i. If this is positive, information is shared predominantly from unit i to j, while negative values indicate the opposite direction. Analogously, we compute the differences in dTE as δTEi,j (cf. Methods and Supplementary Note 1). The set of pairs {δMIi,j} or {δTEi,j} for all i, j then capture strength and directionality of information routing in the network akin to a functional connectivity analysis in neuroscience39. We refer to them as IRPs.

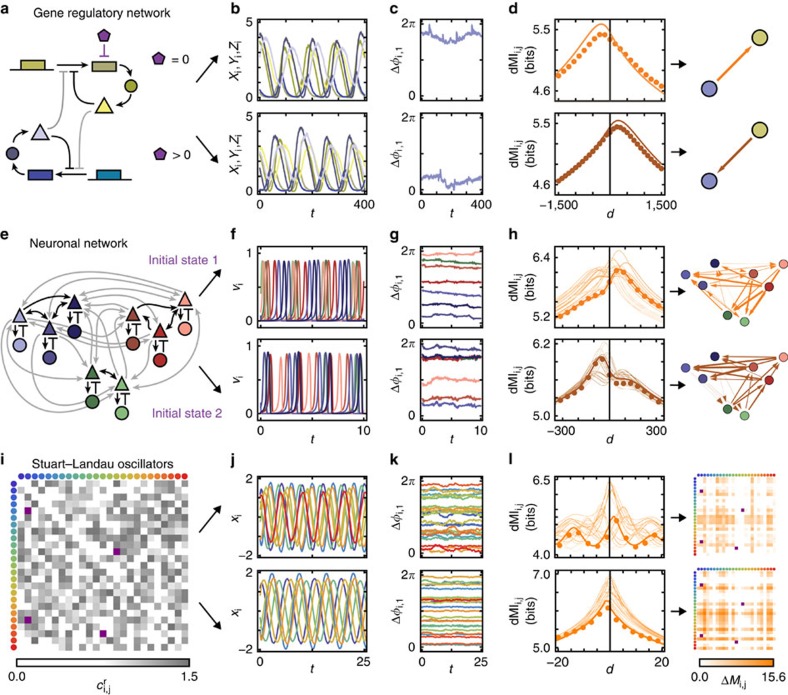
A range of networks of oscillatory units, with disparate physical interactions, connection topologies and external input signals support multiple IRPs. For instance, in a model of a gene-regulatory network with two oscillatory sub-networks (Fig. 1a) dMI analysis reveals IRPs with different dominant directions (Fig. 1b–d, upper versus lower). The change is triggered by adding an external factor that degrades the transcribed mRNA in one of the oscillators and thereby changes its intrinsic frequency (see Methods). More complex changes in IRPs emerge in larger networks, possibly with modular architecture. In a network of interacting neuronal populations (Fig. 1e), different initial conditions lead to different underlying collective dynamical states. Switching between them induces complicated but specific changes in the IRPs (Fig. 1f–h). Different IRPs also emerge by changing a small number of connections in larger networks. Fig. 1i–l illustrates this for a generic system of coupled oscillators each close to a Hopf bifurcation.

Figure 1. Flexible information routing across networks.

Figure 1

Open in a new tab

(a) Simple model of a gene-regulatory network of two coupled biochemical oscillators of Goodwin type (yellow and blue). An additional molecule (purple) degrades the transcribed mRNA in one of the oscillators and thereby changes its intrinsic frequency. Coupling strengths are gray coded (darker colour indicates stronger coupling), sharp arrows indicate activating and blunt arrows inhibiting influences (cf. Methods). (b) Stochastic oscillatory dynamics of the concentrations of the systems components xi (mRNA), yi (enzyme), and zi (protein), i∈{1, 2}. (c) Fluctuations of the phases extracted from the full dynamics relative to a reference unit. (d) dMI (dMI1,2) between the phase signals. The numerical data (dots) agrees well with the theoretical prediction (4) (solid lines). The asymmetry in the dMI curves around d=0 indicates a directed information sharing pattern summarized in the graphs (right). Arrow thickness indicates the strength of directed information sharing ΔMIi,j measured by the positively rectified differences of the areas below the dMIi,j(d) curve for d<0 and d>0. (e–h) Same as in a–d but for a modular network of coupled neuronal sub-populations consisting each of excitatory (triangle) and inhibitory (disk) populations (Wilson–Cowan-type dynamics) that undergo neuronal oscillatory activity (cf. Methods). For the same network two different collective dynamical states accessed by different initial conditions give rise to two different information sharing patterns (f–h top versus bottom). (f) Oscillatory activities vi of the N=8 excitatory populations i. (i–l) As in a–d but for generic oscillators close to a Hopf bifurcation (Stuart–Landau oscillators) each described by two-dimensional normal-form coordinates (xi,yi) connected to a larger network of N=25 oscillators with coupling coefficients ci,jr (cf. Methods). In i and l, connectivity matrices are shown instead of graphs. Two different network-wide IRPs arise (top versus bottom in j–l) by changing a small number of connection weights (purple entries in i and l).

In general, several qualitatively different options for modifying network-wide IRPs exist, all of which are relevant in natural and artificial systems: (i) changing the intrinsic properties of individual units (Fig. 1a–d); (ii) modifying the system connectivity (Fig. 1i–l); and (iii) selecting distinct dynamical states of structurally the same system (Fig. 1e–h).

Theory of phase information routing

To reveal how different IRPs arise and how they depend on the network properties and dynamics, we derive analytic expressions for the dMI and dTE between all pairs of oscillators in a network. We determine the phase of each oscillator i in isolation by extending its phase description to the full basin of attraction of the stable limit cycle8,40. For weak coupling, the effective phase evolution becomes

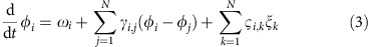graphic file with name ncomms11061-m4.jpg

where ωi is the intrinsic oscillation frequencies of node i and the coupling functions γi,j(·) depend on the phase differences only. The final sum in (3) models external signals as independent Gaussian white noise processes ξk and a covariance matrix ςi,k. The precise forms of γi,j(·) and ςi,k generally depend on the specific system (Supplementary Note 3).

As visible from Fig. 1e–h, the IRP strongly depends on the underlying collective dynamical state. We therefore decompose the dynamics into a deterministic reference part 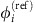Inline graphic and a fluctuating component 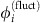Inline graphic. We focus on phase-locked configurations for the deterministic dynamics with constant phase offsets 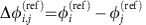Inline graphic. We estimate the stochastic part 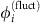Inline graphic via a small-noise expansion (Methods and Supplementary Note 4, Theorem 1) yielding a first-order approximation for the joint probabilities pi,j(d). Using (2) together with the periodicity of the phase variables, we obtain the dMI

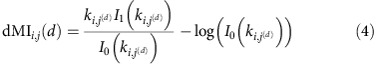graphic file with name ncomms11061-m9.jpg

between phase signals in coupled oscillatory networks; here, In(k) is the nth modified Bessel function of the first kind, and ki,j(d) is the inverse variance of a von Mises distributions ansatz for pi,j(d). The system's parameter dependencies, including different inputs, local unit dynamics, coupling functions and interaction topologies are contained in ki,j(d). By similar calculations we obtain analytical expressions for dTEi→j (Methods and Supplementary Note 4, Theorem 2). Our theoretical predictions well match the numerical estimates (Fig. 1d,h,l, see also Fig. 2c,d below and Supplementary Figs 1 and 2). For independent input signals (ςi,k=0 for i≠k) we typically obtain similar IRPs determined either by the dMI or the transfer entropy (Supplementary Fig. 1). Further, the results remain valid qualitatively when the noise level increases (Supplementary Fig. 2).

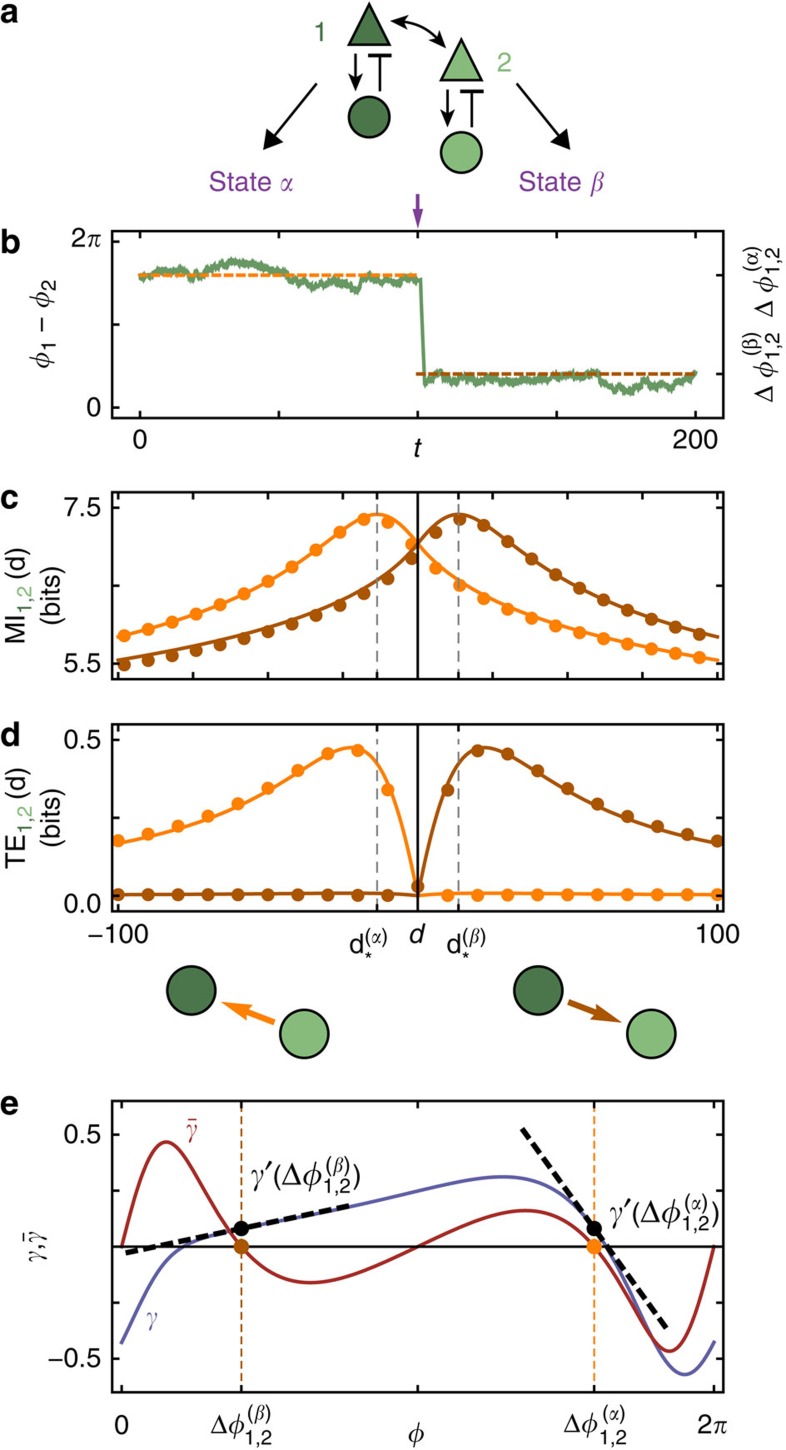
Figure 2. Multi-stable dynamics and anisotropic information routing.

Figure 2

Open in a new tab

(a) Two identical and symmetrically coupled neuronal circuits of Wilson–Cowan-type (dark and light green, modular sub-network in Fig. 1e). The noise free (that is, input free) network displays two different stable oscillatory dynamical states α and β. (b) Phase difference Δφ1,2(t):=φ1(t)−φ2(t) between the extracted phases of the two neuronal populations is fluctuating around a locked value 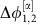Inline graphic of a the stable collective state α of the deterministic system (orange); a strong external perturbation (purple arrow) induces a switch to stochastic dynamics around the second stable deterministic reference state β (brown) with phase difference 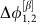Inline graphic. (c) Delayed mutual information dMI1,2 and (d) transfer entropy dTE1→2 curves between the phase signals in states α (orange) and β (brown) for numerical data (dots) and theory (lines) as a function of the time delay d between the stochastic phase signals φ1(t) and φ2(t+d). 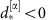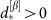The change in peak latencies form Inline graphic to Inline graphic in the dMI1,2 curves and the asymmetry of the dTE1→2 curves show anisotropic information routing for the two different states. Switching between the two dynamical states reverses the effective information routing pattern (IRP) (graphs, bottom). (e) Phase coupling function γ(Δφ)=γ1,2(Δφ)=γ2,1(Δφ) (blue) between the two neuronal oscillators and its anti-symmetric part 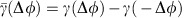Inline graphic (red). 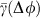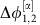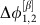The two zeros of Inline graphic with negative slope indicate the stable deterministic equilibrium phase differences Inline graphic and Inline graphic of the dynamical states α and β, receptively. The directionality in the IRP arises due to symmetry breaking in the dynamics reflected in the different slopes of γ(Δφ) (dashed lines): In the state α, oscillator 1 receives inputs from oscillator 2 proportional to 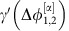Inline graphic, while oscillator 2 is coupled to 1 proportional to 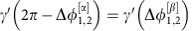Inline graphic in linear small-noise approximation (cf. equation (5)). As 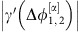Inline graphic is large deviations from the phase-locked state of oscillator 2 due to the noise inputs are strongly propagated to oscillator 1 to restore the phase-locking. Information injected to oscillator 2 is thus transmitted to oscillator 1. In contrast, inputs to oscillator 1 only weakly impact oscillator 2 as 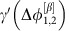Inline graphic is small. In total, the information is thus dominantly routed from 2 to 1. Switching to the dynamical state β reverses the roles of the oscillators and thus also the directionality of the information routing motive.

Mechanism of anisotropic information routing

To better understand how a collective state gives rise to a specific routing pattern with directed information sharing and transfer, consider a network of two symmetrically coupled identical neural population models (Fig. 2a). Because of permutation symmetry, the coupling functions γi,j, obtained from the phase reduction of the original Wilson–Cowan-type equations41 (Methods, Supplementary Note 3), are identical. For biologically plausible parameters this network in the noiseless-limit has two stable phase-locked reference states (α and β). 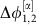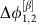The fixed phase differences Inline graphic and Inline graphic are determined by the zeros of the anti-symmetric coupling 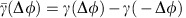Inline graphic with negative slope (Fig. 2e). For a given level of (sufficiently weak) noise, the system shows fluctuations around either one of these states (Fig. 2b) each giving rise to a different IRP. Sufficiently strong external signals can trigger state switching and thereby effectively invert the dominant communication direction visible from the dMI (Fig. 2c) and even more pronounced from the dTE (Fig. 2d) without changing any structural properties of the network.

The anisotropy in information transfer in the fully symmetric network is due to symmetry broken dynamical states. For independent noise inputs, ςi,k=ςiδi,k, that are moreover small, the evolution of 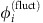Inline graphic, i∈{1,2}, near the reference state α reduces to

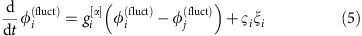graphic file with name ncomms11061-m14.jpg

with coupling constants 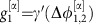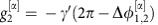Inline graphic, Inline graphic (Methods). As 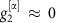Inline graphic (Fig. 2e), the phase 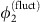Inline graphic essentially freely fluctuates driven by the noise input ς2ξ2. This causes the system to deviate from the equilibrium phase difference 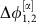Inline graphic. At the same time, the strongly negative coupling 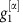Inline graphic dominates over the noise term ς1ξ1 and unit 1 is driven to restore the phase difference by reducing 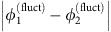Inline graphic. Thus, 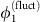Inline graphic is effectively enslaved to track 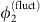Inline graphic and information is routed from unit 2 to 1, reflected in the dMI and dTE curves. The same mechanism accounts for the reversed anisotropy in communication when the system is near state β as the roles of units 1 and 2 are exchanged. Calculating the peak of the dMI curve in this example also provides a time scale 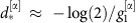Inline graphic at which maximal information sharing is observed (Methods, equation (10), see also Supplementary Note 4). It furthermore becomes clear that the directionality of the information transfer in general need not be related to the order in which the oscillators phase-lock because the phase-advanced oscillator can either effectively pull the lagging one, or, as in this example, the lagging oscillator can push the leading one to restore the equilibrium phase-difference.

In summary, effective interactions local in state space and controlled by the underlying reference state together with the noise characteristics determine the IRPs of the network. Symmetry broken dynamical states then induce anisotropic and switchable routing patterns without the need to change the physical network structure.

Information routing in networks of networks

For networks with modular interaction topology24,25,26,27,28, our theory relating topology, collective dynamics and IRPs between individual units can be generalized to predict routing between entire modules. Assuming that each sub-network X in the noiseless limit has a stable phase-locked reference state, a second-phase reduction23 generalized to stochastic dynamics characterizes each module by a single meta-oscillator with collective phase ΦX and frequency ΩX, driven by effective noise sources ΞX with covariances ΣX,Y. The collective phase dynamics of a network with M modules then satisfies

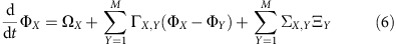graphic file with name ncomms11061-m25.jpg

where ΓX,Y are the effective inter-community couplings (Supplementary Note 5). The structure of equation (6) is formally identical to equation (3) so that the expressions for inter-node information routing (dMIi,j and dTEi→j) can be lifted to expressions on the inter-community level (dMIX,Y and dTEX→Y) by replacing node- with community-related quantities (that is, ωi with ΩX or γik with ΓX,K and so on; Supplementary Note 5, Corollaries 3 and 4). Importantly, this process can be further iterated to networks of networks and so on. Figure 3 shows examples of information flow patterns resolved at two scales. The information routing direction on the larger scale reflects the majority and relative strengths of IRPs on the finer scale.

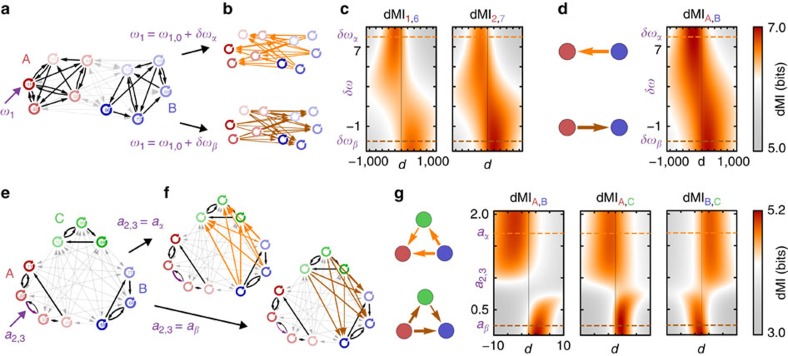
Figure 3. Remotely induced rerouting of information in modular networks.

Figure 3

Open in a new tab

(a) Network with two coupled communities A and B (red and blue) of oscillators close to a Hopf bifurcation. Changing the intrinsic frequency of a single node i=1 from ω1+δωα to ω1+δωβ induces a collective reorganization of equilibrium phase differences, that result in b oppositely directed information sharing patterns between the individual nodes of the two modules (top versus bottom). (c) dMI between two pairs of nodes from the two different clusters as a function of the time delay d and frequency change δω1 of oscillator 1. The change of the peak from positive to negative delays reflecting the inversion of the information routing is visible. (d) Information routing patterns (IRPs) calculated from the hierarchically reduced system for the two configurations in b (left) and as a function of δω1 (right) reflect the inversion on the finer scale (b,c). (e) Hierarchical network of three coupled modules of phase oscillators. (f) A change in the connection strength a2,3 from aα to aβ between two nodes (3A→2A) in sub-network A induces an inversion of information routing direction between the remote sub-networks B and C. (g) Full IRPs calculated form the hierarchical reduced system for a2,3=aα and a2,3=aα (left) and as a function of a2,3 for all pairs of modules (density plots, right). The transition is not continuous but rather switch like.

Nonlocal information rerouting via local interventions

The collective quantities in the system (6) are intricate functions of the network properties at the lower scales. Intriguingly, the coupling functions ΓX,Y not only depend on the nonlocal interactions 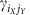Inline graphic between units iX of module X and jY of cluster Y but also on purely local properties of the individual clusters. 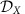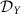In particular, the form of ΓX,Y is a function of the intrinsic local dynamical states Inline graphic and Inline graphic of both clusters as well as the phase response ZX of sub-network X (see Methods and Supplementary Note 5). Thus IRPs on the entire network level depend on local community properties. This establishes several generic mechanisms to globally change information routing in networks via local changes of modular properties, local connectivity or via switching of local dynamical states.

In a network consisting of two sub-networks (Fig. 3a) the local change of the frequency of a single Hopf-oscillator in sub-network A induces a nonlocal inversion of the information routing between cluster A and B (Fig. 3b–d). In Fig. 3e–f, the direction in which information is routed between two sub-networks B and C of coupled phase oscillators is remotely changed by increasing the strength of a local link in module A. The origin in both examples is a non-trivial combination of several factors: the (small) manipulations alter the collective cluster frequency ΩA and the local dynamical state 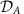Inline graphic which in turn changes the collective phase response ZA and the effective noise strength ΞA of cluster A. These changes all contribute to changes in the effective couplings ΓX,Y as well as in the inter-cluster phase-locking values ΔΦX,Y=ΦX−ΦY (cf. Supplementary Note 5 and Supplementary Fig. 3). The changes in these properties, which enter the expressions for the information sharing and routing measures (Fig. 2 and Supplementary Note 4) then cause the observed changes in information routing direction. Interestingly, the transition in information routing has a switch-like dependency on the changed parameter (Fig. 3c,d,g) promoting digital like changes of communication modes. Combinatorially many information routing patterns.

Combinatorial many information routing patterns

As an alternative to interventions on local properties, also switching between multi-stable local dynamical states 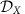Inline graphic can induce global information rerouting. In the example in Fig. 4, each of the M=3 modules X∈{A, B, C} exhibits 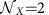Inline graphic alternative phase-locked states (labelled αX and βX, Supplementary Section 6 and Supplementary Fig. 4). For sufficiently weak coupling, this local multi-stability is preserved in the dynamics of the entire modular network. Consequently each choice of the 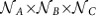Inline graphic possible combinations of ‘local' states gives rise to at least one network-wide collective state. Certain combinations of local states can give rise to one or even multiple globally phase-locked states (for example, [αAβBαC] in Fig. 4). Others support non-phase-locked dynamics that gives rise to time-dependent IRPs (cf. Fig. 4c and below). Thus, varying local dynamical states in a hierarchical network flexibly produces a combinatorial number 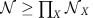Inline graphic of different IRPs in the same physical network.

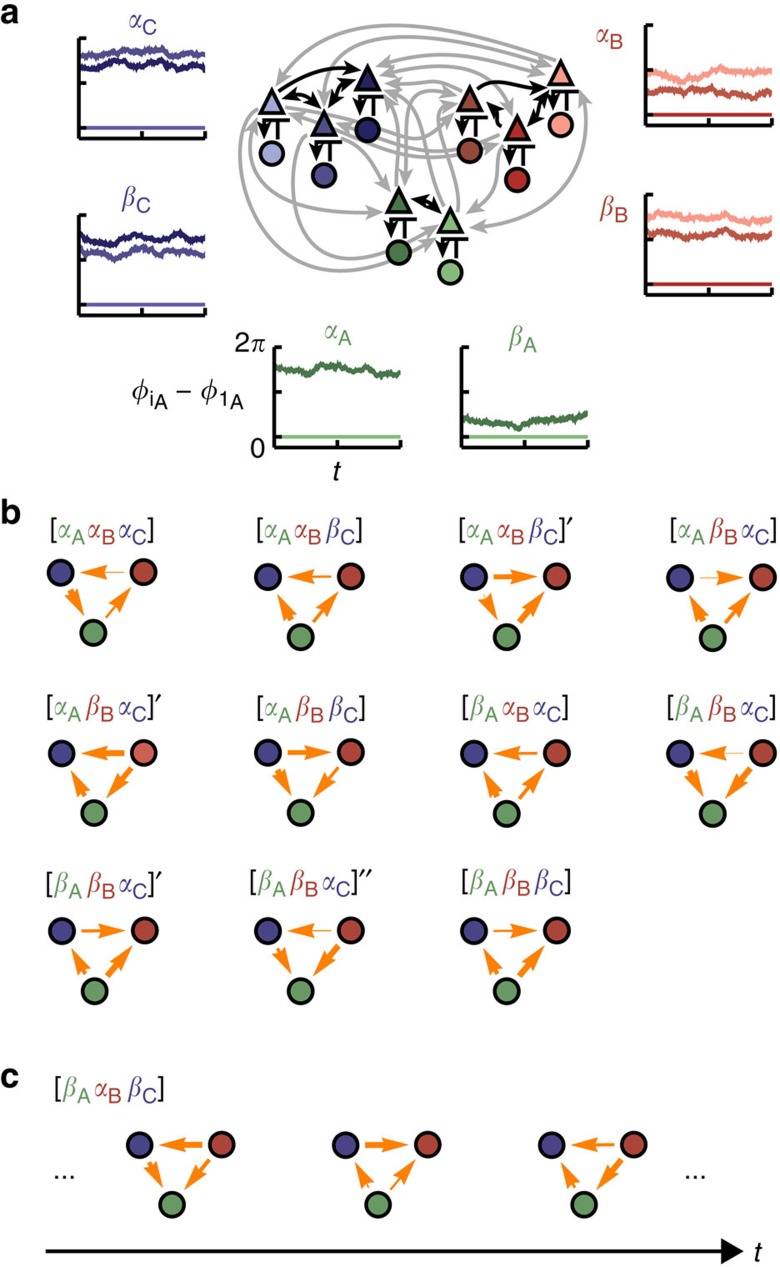
Figure 4. Combinatorially many IRPs in networks with locally multi-stable dynamics.

Figure 4

Open in a new tab

(a) Modular circuit as in Fig. 1e. Without inter-module coupling (grey arrows), each of the M=3 communities X∈{A, B, C} exhibits multi-stability between two phase-locked configurations, denoted as states αX and βX (insets). The characteristics of these states remain present in the full network once weak coupling between the modules is introduced. We refer to these states as local dynamical states 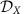Inline graphic. (b) Information routing patterns (IRPs) between the hierarchically reduced sub-networks for different combinations of the local dynamical states 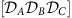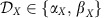Inline graphic, Inline graphic that give rise to globally phase-locked dynamics. Arrows between nodes X and Y indicate strength (line width) and sign (arrow direction) of the information routing quantified via the difference in integrated dTE curves between the nodes (see Methods). The same combination of local dynamical states (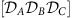Inline graphic) can give rise to more than one globally phase-locked collective state marked with dashes, i.e. 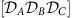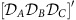Inline graphic, Inline graphic,…. each giving rise to a separate IRP: For fixed local dynamical states the global network is multi-stable and choosing between those components is changing the information routing similarly as in Fig. 2. (c) The local dynamical state configuration [βAαBβC] generates a periodic global dynamical state (cf. Supplementary Fig. 3) in which the hierarchically reduced IRP (graphs) becomes time-dependent (cf. also Supplementary Note 6).

Time-dependent information routing

General reference states, including periodic or transient dynamics, are not stationary and hence the expressions for the dMI and dTE become dependent on the time t. For example, Fig. 4c shows IRPs that undergo cyclic changes due to an underlying periodic reference state (cf. also Supplementary Note 6 and Supplementary Fig. 5a-c). In systems with a global fixed point, systematic displacements to different starting positions in state space give rise to different stochastic transients with different and time-dependent IRPs (Supplementary Fig. 5d). Similarly, switching dynamics along heteroclinic orbits constitute another way of generating specific progressions of reference dynamics. Thus information ‘surfing' on top of non-stationary reference dynamical configurations naturally yield temporally structured sequences of IRPs, resolvable also by other measures of instantaneous information flow36,42,43.

Discussion

The above results establish a theoretical basis for the emergence of information routing capabilities in complex networks when signals are communicated on top of collective reference states. We show how information sharing (dMI) and transfer (dTE) emerge through the joint action of local unit features, global interaction topology and choice of the collective dynamical state. We find that IRPs self-organize according to general principles (cf. Figs 2, 3, 4) and can thus be systematically manipulated. Employing formal identity of our approach at every scale in oscillatory modular networks (equations (3) versus (6), ) we identify local paradigms that are capable of regulating information routing at the nonlocal level across the whole network (Figs 3 and 4).

In contrast to self-organized technological routing protocols where local nodes use local routing information to locally propagate signals, such as in peer-to-peer networks44, in the mechanism studied here the information routing modality is set by the entire network's collective dynamics. This collective reference state typically evolves on a slower timescale than the information carrying fluctuations that surf on top of it and is thus different from signal propagation in cascades45 or avalanches46 that dominate on shorter time scales.

We derived theoretical results based on information sharing and transfer obtained via delayed mutual information and transfer entropy curves. Using these abstract measures our results are independent of any particular implementation of a communication protocol and thus generically demonstrate how collective dynamics can have a functional role in information routing. For example, in the network in Fig. 2 externally injected streams of information are automatically encoded in fluctuations of the rotation frequency of the individual oscillators. The injected signals are then transmitted through the network and decodable from the fluctuating phase velocity of a target unit precisely along those pathways predicted by the current state-dependent IRP (Supplementary Note 7 and Supplementary Figs 6 and 7).

Our theory is based on a small-noise approximation that conditions the analysis onto a specific underlying dynamical state. In this way, we extracted the precise role of such a reference state for the network's information routing abilities. For larger signal amplitudes or in highly recurrent networks, in which higher order interactions can play an important role the expansion can be carried out systematically to higher orders using diagrammatic approaches47 or numerically to accounting for better accuracy and non-Gaussian correlations (cf. also Supplementary Note 4).

In systems with multi-stable states two signal types need to be discriminated: those that encode the information to be routed and those that indicate a switch in the reference dynamics and consequently the IRPs. If the second type of stimuli is amplified appropriately a switch between multi-stable states can be induced that moves the network into the appropriate IRP state for the signals that follow. For example, in the network of Fig. 2a switch from states α to β can be induced by a strong positive pulse to oscillator 2 (and vice versa). If such pulses are part of the input a switch to the appropriate IRP state will automatically be triggered and the network auto-regulates its IRP function (Supplementary Fig. 6). More generally a separate part of the network that effectively filters out relevant signatures indicating the need for a different IRP could provide such pulses. Using the fact that local interventions are capable to switch IRPs in the network also the outcomes of local computations can be used to trigger changes in the global information routing and thereby enable context-dependent processing in a self-organized way.

When information surfs on top of dynamical reference states the control of IRPs is shifted towards controlling collective network dynamics making methods from control theory of dynamical systems available to the control of information routing. For example, changing the interaction function in coupled oscillators systems18 or providing control signals to a subset of nodes48,49 are capable of manipulating the network dynamics. Moreover, switch-like changes (cf. Fig. 3) can be triggered by crossing bifurcation points and the control of IRPs then gets linked to bifurcation theory of network dynamical systems.

While the mathematical part of our analysis focused on phase signals, including additional amplitude degrees of freedom into the theoretical framework can help to explore neural or cell signalling codes that simultaneously use activity- and phase-based representations to convey information50. Moreover, separating IRP generation, for example, via phase configurations, from actual information transfer, for instance in amplitude degrees of freedom, might be useful for the design of systems with a flexible communication function.

The role of self-organized collective dynamics in information routing in biological systems is still speculative. Our theoretical study, identifying natural mechanisms for state-dependent sharing and transfer of information, may thus foster further experimental explorations that seek for conclusive proofs and exploring the nonlocal effects of local system manipulations. While recent experimental studies point towards functional roles of collective dynamics31,35,51,52,53,54 the predicted phenomena, including nonlocal changes of information routing by local interventions, could be directly experimentally verified using methods available to date, such as synthetic patterned neuronal cultures55, electrochemical arrays18 or synthetic gene-regulatory networks5 (Supplementary Note 8). In addition, our results are applicable to the inverse problem: Unknown network characteristics may be inferred by fitting theoretically expected dMI and dTE patterns to experimentally observed data. For example, inferring state-dependent coupling strengths could further the analysis of neuronal dynamics during context-dependent processing33,35,39,53,54,56.

Modifying inputs, initial conditions or system-intrinsic properties may well be viable in many biological and artificial systems whose function requires particular information routing. For instance, on long time scales, evolutionary pressure may select a particular IRP by biasing a particular collective state in gene-regulatory and cell-signalling networks2,15,57; on intermediate time scales, local changes in neuronal responses due to adaptation or varying synaptic coupling strength during learning processes13 can impact information routing paths in entire neuronal circuits; on fast time scales, defined control inputs to biological networks or engineered communication systems that switch the underlying collective state, can dynamically modulate IRPs without any physical change to the network.

Methods

Transfer entropy

The dTE22 from a time-series xi(t) to a time-series xj(t) is defined as

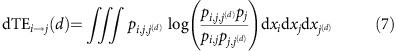graphic file with name ncomms11061-m34.jpg

with joint probability pi,j,j(d)=p(xj(t+d), xi(t), xj(t)) and pj,j(d)=p(xj(t+d), xj(t)). This expression is not invariant under permutation of i and j, implying the directionality of TE. For a more direct comparison with dMI in Fig. 2, we define dTEi,j(d) by dTEi→j(d) for d>0 and by dTEj→i(−d) for d<0 (cf. Supplementary Note 1 for additional details).

Dynamic information routing via dynamical states

For a dynamical system (2) the reference deterministic solution x(ref)(t+s) starting at x(t) is given by the deterministic flow x(ref)(t+s)=F(ref)(x(t), s). The small-noise approximation for white noise ξ yields

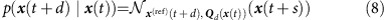graphic file with name ncomms11061-m35.jpg

where 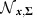Inline graphic denotes the normal distribution with mean x and covariance matrix Σ, 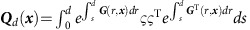Inline graphic and G(s, x)=Df (F(x, s)). We assumed G(s, x)G(t,x)=G(t, x)G(s, x). From this and the initial distribution p(x(t)), the dMI and transfer entropy dMIi,j(d, t) and dTEi→j(d, t) are obtained via (2) and (7). The result depends on time t, lag d and the reference state x(ref) (cf. Supplementary Note 2 for additional details).

Oscillator networks

In Fig. 1a, we consider a network of two coupled biochemical Goodwin oscillators14,58. Oscillations in the expression levels of the molecular products arise because of a nonlinear repressive feedback loop in successive transcription, translation and catalytic reactions. The oscillators are coupled via mutual repression of the translation process59. In addition, in one oscillator changes in concentration of an external enzyme regulate the speed of degradation of mRNAs, thus affecting the translation reaction, and, ultimately, the oscillation frequency. In Figs 1e, 2 and 4 we consider networks of Wilson–Cowan-type neural masses (population signals)41. Each neural mass intrinsically oscillates because of antagonistic interactions between local excitatory and inhibitory populations. Different neural masses interact, within and between communities, via excitatory synapses. In the generic networks in Figs 1i and 3a each unit is modelled by the normal form of a Hopf-bifurcation in the oscillatory regime together with linear coupling. Finally, the modular networks analysed in Fig. 3a,b are directly cast as phase-reduced models with freely chosen coupling functions. See the Supplementary Note 8 and Supplementary Figs 4, 8 and 9 for additional details, model equations and parameters and phase estimation.

Analytic derivation of the dMI and dTE curves

In the small-noise expansion60, both dMI and dTE curves have an analytic approximation: For stochastic fluctuations around some phase-locked collective state with constant reference phase offsets Δφi,j=φi−φj the phases evolve as 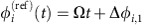Inline graphic in the deterministic limit, where Ω=ωi+∑kγi,k(Δφi,k) is the collective network frequency and the γi,j(·) are the coupling functions from equation (3). In presence of noise, the phase dynamics have stochastic components 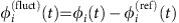Inline graphic. In first-order approximation, independent noise inputs ςi,j=ςiδi,j yield coupled Ornstein–Uhlenbeck processes

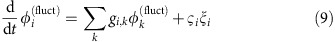graphic file with name ncomms11061-m40.jpg

with linearized, state-dependent couplings given by the Laplacian matrix entries gi,j=−γ′i,j(Δφi,j) and 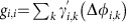Inline graphic. The analytic solution to the stochastic equation (9) provides an estimate of the probability distributions, pi, pi,j(d) and pi,j,j(d). Via (2) this results in a prediction for dMIi,j(d), equation (4), as a function of the matrix elements ki,j(d) specifying the inverse variance of a von Mises distribution ansatz for pi,j(d). Similarly via (7) an expression for dTEi→j(d) is obtained. For the dependency of 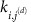Inline graphic, and dTEi→j(d) on network parameters and further details, see the derivation of the theorems 1 and 2 in Supplementary Note 4.

Time scale for information sharing

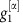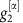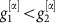For a network of two oscillators as in Fig. (2) with linearized coupling strengths Inline graphic and Inline graphic and Inline graphic, maximizing dMI1,2(d) (see Supplementary Note 4 for full analytic expressions of dMI and dTE in two oscillator networks) yields

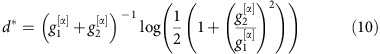graphic file with name ncomms11061-m46.jpg

Collective phase reduction

Suppose that each node i=iX belongs to a specific network module X out of M≤N non-overlapping modules of a network. Then equation (3) can be simplified to equation (6) under the assumption that in the absence of noise every community X has a stable internally phase-locked state 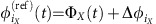Inline graphic, where 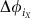Inline graphic are constant phase offsets of individual nodes iX. Every community can then be regarded as a single meta-oscillator with a collective phase ΦX(t) and a collective frequency 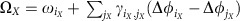Inline graphic. The vector components of the collective phase response ZX, the effective couplings ΓX,Y and the noise parameters ΣX,Y and ΞX are obtained through collective phase reduction and depend on the respective quantities (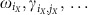Inline graphic) on the single-unit scale (see Supplementary Note 5 for a full derivation).

Additional information

How to cite this article: Kirst, C. et al. Dynamic information routing in complex networks. Nat. Commun. 7:11061 doi: 10.1038/ncomms11061 (2016).

Supplementary Material

Supplementary

Supplementary Figures 1-10, Supplementary Notes 1-8 and Supplementary References.

ncomms11061-s1.pdf (5.9MB, pdf)

Acknowledgments

We thank T. Geisel for valuable discussions. Partially supported by the Federal Ministry for Education and Research (BMBF) under grants no. 01GQ1005B (C.K., D.B., M.T.) and 03SF0472E (M.T.), by the NVIDIA Corp., Santa Clara, USA (M.T.), a grant by the Max Planck Society (M.T.), by the FP7 Marie Curie career development fellowship IEF 330792 (DynViB) (D.B.) and an independent postdoctoral fellowship by the Rockefeller University, New York, USA (C.K.).

Footnotes

Author contributions All authors designed research. C.K. worked out the theory and derived the analytical results, developed analysis tools and carried out the numerical experiments. All authors analysed the data, interpreted the results and wrote the manuscript.

References

  1. Tyson J. J., Chen K. & Novak B. Network dynamics and cell physiology. Nat. Rev. Mol. Cell Biol. 2, 908–916 (2001). [DOI] [PubMed] [Google Scholar]
  2. Tkacik G., Callan C. G. & Bialek W. Information flow and optimization in transcriptional regulation. Proc. Natl Acad. Sci. USA 105, 12265–12270 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Tononi G., Edelman G. M. & Sporns O. Complexity and coherency: integrating information in the brain. Trends Cogn. Sci. 2, 474–484 (1998). [DOI] [PubMed] [Google Scholar]
  4. Weber W., Rabaey J. M., Aarts E. (eds.) Ambient Intelligence Springer (2005). [Google Scholar]
  5. Stricker J. et al. A fast, robust and tunable synthetic gene oscillator. Nature 456, 516–519 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Varela F., Lachaux J.-P., Rodriguez E. & Martinerie J. The brainweb: phase synchronization and large-scale integration. Nat. Rev. Neurosci. 2, 229–239 (2001). [DOI] [PubMed] [Google Scholar]
  7. Winfree A. T. The Geometry of Biological Time Springer (1980). [Google Scholar]
  8. Kuramoto Y. Chemical Oscillations, Waves, and Turbulence Springer (1984). [Google Scholar]
  9. Strogatz S. H. Exploring complex networks. Nature 410, 268–276 (2001). [DOI] [PubMed] [Google Scholar]
  10. Pikovsky A. S., Rosenblum M. & Kurths J. Synchronization—A Universal Concept in Nonlinear Sciences Cambridge University Press (2001). [Google Scholar]
  11. Acebrón J., Bonilla L. & Vicente C. The Kuramoto model: a simple paradigm for synchronization phenomena. Rev. Mod. Phys. 77, 137–185 (2005). [Google Scholar]
  12. Fries P. A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends. Cogn. Sci. 9, 474–480 (2005). [DOI] [PubMed] [Google Scholar]
  13. Salazar R. F., Dotson N. M., Bressler S. L. & Gray C. M. Content-specific fronto-parietal synchronization during visual working memory. Science 338, 1097–1100 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Goldbeter A. Computational approaches to cellular rhythms. Nature 420, 238–245 (2002). [DOI] [PubMed] [Google Scholar]
  15. Feillet C. et al. Phase locking and multiple oscillating attractors for the coupled mammalian clock and cell cycle. Proc. Natl Acad. Sci. USA 111, 9828–9833 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Blasius B., Huppert A. & Stone L. Complex dynamics and phase synchronization in spatially extended ecological systems. Nature 399, 354–359 (1999). [DOI] [PubMed] [Google Scholar]
  17. Néda Z., Ravasz E., Brechet Y., Vicsek T. & Barabási A. L. The sound of many hands clapping. Nature 403, 849–850 (2000). [DOI] [PubMed] [Google Scholar]
  18. Kiss I. Z., Rusin C. G., Kori H. & Hudson J. L. Engineering complex dynamical structures: sequential patterns and desynchronization. Science 316, 1886–1889 (2007). [DOI] [PubMed] [Google Scholar]
  19. Klinglmayr J., Kirst C., Bettstetter C. & Timme M. Guaranteeing global synchronization in networks with stochastic interactions. New. J. Phys. 14, 073031 (2012). [Google Scholar]
  20. Shaw R. S. Strange attractors, chaotic behavior, and information flow. Zeitschr. f. Naturforsch. 36, 80–112 (1981). [Google Scholar]
  21. Vastano J. A. & Swinney H. L. Information transport in spatiotemporal systems. Phys. Rev. Lett. 18, 1773–1776 (1988). [DOI] [PubMed] [Google Scholar]
  22. Schreiber T. Measuring information transfer. Phys. Rev. Lett. 85, 461–464 (2000). [DOI] [PubMed] [Google Scholar]
  23. Kawamura Y., Nakao H., Arai K., Kori H. & Kuramoto Y. Collective phase sensitivity. Phys. Rev. Lett. 101, 024101 (2008). [DOI] [PubMed] [Google Scholar]
  24. Newman M. E. J. Communities, modules and large-scale structure in networks. Nat. Phys. 7, 25–31 (2011). [Google Scholar]
  25. Pajevic S. & Plenz D. The organization of strong links in complex networks. Nat. Phys. 8, 429–436 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Song S., Sjöström P. J., Reigl M., Nelson S. & Chklovskii D. B. Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 3, e68 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Perin R., Berger T. K. & Markram H. A synaptic organizing principle for cortical neuronal groups. Proc. Natl Acad. Sci. USA 108, 5419–5424 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Hagmann P. et al. Mapping the structural core of human cerebral cortex. PLoS Biol. 6, e159 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Ravasz E., Somera A. L., Mongru D. A., Oltvai Z. N. & Barabási A.-L. Hierarchical Organization of modularity in metabolic networks. Science 297, 1551–1555 (2002). [DOI] [PubMed] [Google Scholar]
  30. McMillen D., Kopell N., Hasty J. & Collins J. J. Synchronizing genetic relaxation oscillators by intercell signaling. Proc. Natl Acad. Sci. USA 99, 679–684 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Cabral J., Hugues E., Sporns O. & Deco G. Role of local network oscillations in resting-state functional connectivity. Neuroimage 57, 130–139 (2011). [DOI] [PubMed] [Google Scholar]
  32. Koepsell K. & Sommer F. T. Information transmission in oscillatory neural activity. Biol. Cybern. 99, 403–416 (2008). [DOI] [PubMed] [Google Scholar]
  33. Kopell N. J., Gritton J. G., Whittington A. W. & Kramer M. A. Beyond the connectome: the dynome. Neuron 83, 1319–1327 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Belitski A. et al. Low-frequency local field potentials and spikes in primary visual cortex convey independent visual information. J. Neurosci. 28, 5696–5709 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Agarwal G. et al. Spatially distributed local fields in the hippocampus encode rat position. Science 344, 626–630 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Lizier J. T., Prokopenko M. & Zomaya A. Y. Local information transfer as a spatiotemporal filter for complex systems. Phys. Rev. E 77, 026110 (2008). [DOI] [PubMed] [Google Scholar]
  37. Lauschke V. M., Charisios D. T., François P. & Aulehla A. Scaling of embryonic patterning based on phase-gradient encoding. Nature 7430, 101–105 (2013). [DOI] [PubMed] [Google Scholar]
  38. Hoppensteadt F. & Izhikevich E. Synchronization of laser oscillators, associative memory, and optical neurocomputing. Phys. Rev. E 62, 4010–4013 (2000). [DOI] [PubMed] [Google Scholar]
  39. Friston K. J. Functional and effective connectivity: a review. Brain Connect. 1, 13–36 (2011). [DOI] [PubMed] [Google Scholar]
  40. Teramae J.-N., Nakao H. & Ermentrout G. B. Stochastic phase reduction for a general class of noisy limit cycle oscillators. Phys. Rev. Lett. 102, 194102 (2009). [DOI] [PubMed] [Google Scholar]
  41. Wilson H. R. & Cowan J. D. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J. 12, 1–24 (1972). [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Liang X. & Kleeman R. Information transfer between dynamical system components. Phys. Rev. Lett. 95, 244101 (2005). [DOI] [PubMed] [Google Scholar]
  43. Majda A. J. & Harlim J. Information flow between subspaces of complex dynamical systems. Proc. Natl Acad. Sci. USA 104, 9558–9563 (2007). [Google Scholar]
  44. Lua E. K., Crowcroft J., Pias M., Sharma R. & Lim S. A survey and comparison of peer-to-peer overlay network schemes. IEEE Commun. Surveys Tutorials 7, 72–93 (2005). [Google Scholar]
  45. Watts D. J. A simple model of global cascades on random networks. Proc. Natl Acad. Sci. USA 99, 5766–5771 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Beggs J. M. & Plenz D. Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11167–11177 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Korutcheva E. & Del Prete V. A diagrammatic approach to study the information transfer in weakly non-linear channels. Int. J. Mod. Phys. B 16, 3527–3544 (2002). [Google Scholar]
  48. Cornelius S. P., Kath W. L. & Motter A. E. Realistic control of network dynamics. Nat. Commun. 4, 1942 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Liu Y.-Y., Slotine J.-J. & Barabási A.-L. Controllability of complex networks. Nature 473, 167–173 (2011). [DOI] [PubMed] [Google Scholar]
  50. Akam T. & Kullmann D. M. Oscillatory multiplexing of population codes for selective communication in the mammalian brain. Nat. Rev. Neurosci. 15, 111–122 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Selimkhanov J. et al. Accurate information transmission through dynamic biochemical signaling networks. Science 346, 1370–1373 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Bastos A. M. et al. Visual areas exert feedforward and feedback influences through distinct frequency channels. Neuron 85, 390–401 (2015). [DOI] [PubMed] [Google Scholar]
  53. Canolty R. T. et al. Oscillatory phase coupling coordinates anatomically dispersed functional cell assemblies. Proc. Natl Acad. Sci. USA 107, 17356–17361 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Cole M. W., Bassett D. S., Power J. D. & Braver T. S. Intrinsic and task-evoked network architectures of the human brain. Neuron 83, 238–251 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Feinerman O., Rotem A. & Moses E. Reliable neuronal logic devices from patterned hippocampal cultures. Nat. Phys. 4, 967–973 (2008). [Google Scholar]
  56. Battaglia D., Witt A., Wolf F. & Geisel T. Dynamic effective connectivity of inter-areal brain circuits. PLoS Comput. Biol. 8, e1002438 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Purvis J. E. & Lahav G. Encoding and decoding cellular information through signaling dynamics. Cell 152, 945–956 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Goodwin B. C. An entrainment model for timed enzyme synthesis in bacteria. Nature 209, 479–481 (1966). [DOI] [PubMed] [Google Scholar]
  59. Wagner A. Circuit topology and the evolution of robustness in two-gene circadian oscillators. Proc. Natl Acad. Sci. USA 102, 11775–11780 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Gardiner C. W. Handbook of Stochastic Methods 3rd edn Springer Verlag (2004). [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary

Supplementary Figures 1-10, Supplementary Notes 1-8 and Supplementary References.

ncomms11061-s1.pdf (5.9MB, pdf)

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES