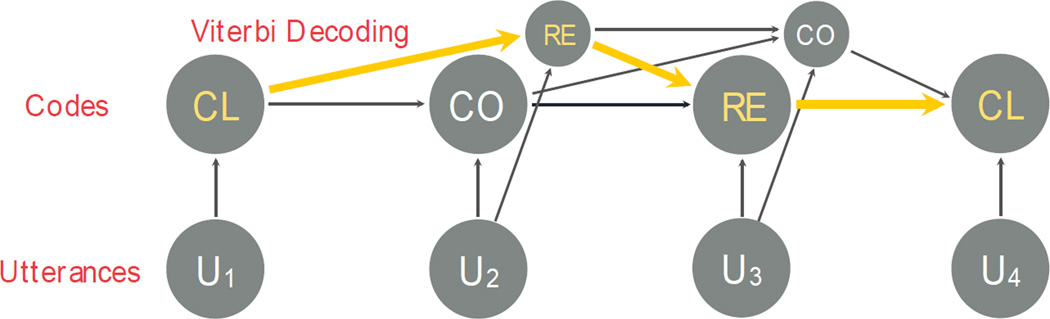
Figure 2.

A graphical representation of the Viterbi decoding process for the sample dialog snippet given in Figure 1. In this example, the Maximum Entropy Markov Model (MEMM) can be thought as a sequence of four logistic regression models: 1) client model, 2) counselor model, 3) counselor model, and 4) client model. The first model uses the client label (given in the transcript) for the first utterance, U₁, to assign the code CL, as there is no alternative client code in our setting. Then the second model uses the decision made for U₁ (i.e., CL) as a binary feature in predicting the code for U₂ (i.e., CO or RE) along with other features extracted for U₂ (n-grams, etc.), assigning probabilities to each decision for the second utterance (e.g. CO/0.6, RE/0.4).

Similarly, the third model uses the decisions made for the first two utterances, U₁ and U₂, as binary features in predicting the code for U₃. Finally the fourth model assigns the code CL to the last utterance, U₄, and the Viterbi algorithm chooses the most likely sequence of codes for the entire dialog (provided in yellow). The Viterbi algorithm allows the model to efficiently evaluate alternative code sequences for earlier utterances that are less likely in isolation but may turn out to be more likely when considered in the context of later utterances. Note that the code for U₂ was first CO (i.e., not a reflection), but was later updated to be RE based on the information from U₃ and U₄.