Figure 3.

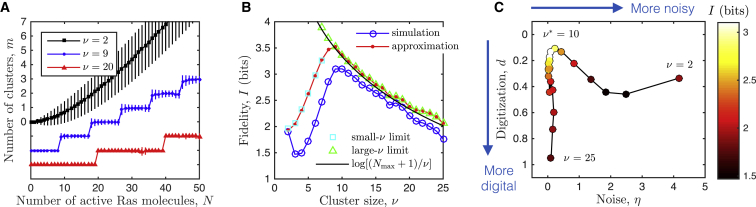
Digital signaling results in an optimal cluster size. (A) The mean input-output response is analog (smooth) for low cluster size (black) and digital (steplike) for high cluster size (red). While increasing the cluster size ν increasingly digitizes the signal, it also decreases the noise. This interplay leads to an optimal cluster size (see B). Data points and error bars show the mean and standard deviation of $p\left(m|N\right)$, respectively. All curves start at m = 0, but two are shifted downward for visual clarity. (B) Fidelity exhibits a maximum at ${\nu }^{\ast }$ due to the tradeoff between noise reduction and state-space reduction. Simulation results (blue circles) are corroborated by the analytic approximation (red line, Eq. 6), as well as expressions in the limits of small ν (cyan squares, Eqs. 8 and 9) and large ν (green triangles, Eq. 4; black line). (C) Increasing the cluster size moves the system through the phase space defined by digitization and noise (compare to Fig. 1A). Noise is reduced $\left(\eta \to 0\right)$, and then the state space is reduced, increasing digitization $\left(d\to 1\right)$. Maximal fidelity occurs at intermediate ν when noise is low, but digitization is not too high. In all panels, parameters are b = 3, $N_{\text{max}}$ = 100, α = 10 s⁻¹, and μ = 10³ s⁻¹, with simulations run for T = 10⁵ s. To see this figure in color, go online.