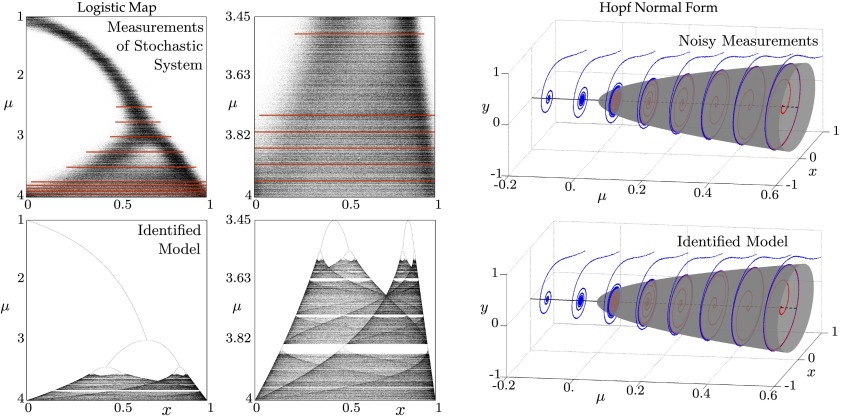
Fig. 3.

SINDy algorithm is able to identify normal forms and capture bifurcations, as demonstrated on the logistic map (Left) and the Hopf normal form (Right). Noisy data from both systems are used to train models. For the logistic map, a handful of parameter values μ (red lines), are used for the training data, and the correct normal form and bifurcation sequence is captured (below). Noisy data for the Hopf normal form are collected at a few values of μ, and the total variation derivative (33) is used to compute time derivatives. The accurate Hopf normal form is reproduced (below). The nonlinear terms identified by the algorithm are in SI Appendix, section 4.4 and Appendix C.