Nanoscale measurements of proton tracks using fluorescent nuclear track detectors

Abstract

Purpose:

The authors describe a method in which fluorescence nuclear track detectors (FNTDs), novel track detectors with nanoscale spatial resolution, are used to determine the linear energy transfer (LET) of individual proton tracks from proton therapy beams by allowing visualization and 3D reconstruction of such tracks.

Methods:

FNTDs were exposed to proton therapy beams with nominal energies ranging from 100 to 250 MeV. Proton track images were then recorded by confocal microscopy of the FNTDs. Proton tracks in the FNTD images were fit by using a Gaussian function to extract fluorescence amplitudes. Histograms of fluorescence amplitudes were then compared with LET spectra.

Results:

The authors successfully used FNTDs to register individual proton tracks from high-energy proton therapy beams, allowing reconstruction of 3D images of proton tracks along with delta rays. The track amplitudes from FNTDs could be used to parameterize LET spectra, allowing the LET of individual proton tracks from therapeutic proton beams to be determined.

Conclusions:

FNTDs can be used to directly visualize proton tracks and their delta rays at the nanoscale level. Because the track intensities in the FNTDs correlate with LET, they could be used further to measure LET of individual proton tracks. This method may be useful for measuring nanoscale radiation quantities and for measuring the LET of individual proton tracks in radiation biology experiments.

1. INTRODUCTION

Fluorescence nuclear track detectors (FNTDs) consist of aluminum oxide crystals doped with carbon and magnesium (Al₂O₃:C,Mg). Ionizing radiation leads to electronic radiochromic transformation of fluorescent color centers within the FNTDs, which are stable at temperatures up to 600 °C. Immediately after irradiation, these fluorescent centers can be excited by a 635-nm laser light, yielding a fluorescence emission centered at 750 nm.^1–3 Fluorescence confocal laser scanning microscopy (FCLSM) can then be used to acquire 3D images of particle tracks within the FNTD volume. FNTDs do not require postirradiation chemical treatment, and a 3D image representation of radiation tracks can be obtained as soon as the radiation traverses the FNTDs. In the absence of optical aberrations, image resolution is limited only by diffraction.

FNTDs are biocompatible and have been used to colocalize individual carbon and neon ion tracks at the single-cell level.^4–7 Those experiments involved culturing cells on the surface of the FNTDs, irradiating the FNTD/cell system, transporting it from the beam line, and fixing and immunostaining the cells for imaging with a commercial FCLSM system.^4–7 The images were then used to extrapolate the trajectory of the track to the position of the cell to infer where the track traversed it.

The experiments described above^4–7 were done with high-linear energy transfer (LET) carbon and neon ion beams, which produce high ionization densities. Here we report using FNTDs to visualize very low-LET (<3 keV/μm) proton therapy beams, and we demonstrate that FNTDs have the potential to measure LET of individual proton tracks or LET spectra of proton beams.

2. METHODS AND MATERIALS

2.A. Fluorescence nuclear track detectors

We used 4 mm × 8 mm × 0.5 mm FNTD chips (Landauer, Inc., Crystal Growth Division, Stillwater, OK)^2,8,9 in which one surface had been polished to optical grade. The FNTDs were preselected by color center concentration by using optical absorption spectroscopy, cleaned with several high purity solvents, and “zeroed” by bleaching with a UV laser scanning system at Landauer.

2.B. Irradiation conditions

FNTD chips were irradiated in a passive scattering nozzle at The University of Texas MD Anderson Cancer Center Proton Therapy Center (Houston, TX, USA) with different energies of unmodulated beams from the passive scattering beam line (Table I). To obtain unmodulated beams, the wheels of the range modulator wheels (RMWs) were parked such that the beam would not pass through any of the RMW steps. Four FNTDs were exposed for each condition at central axis. Slabs of plastic (457-CTI, Gammex, Inc., Middleton, WI, USA) were used in front of the FNTDs to obtain different energies.

TABLE I.

Proton beam parameters for FNTD chip exposures. Irradiation was done with the medium snout at 5 cm from isocenter, source to surface distance setup, 18 cm × 18 cm field size, and unmodulated beams. Slabs of plastic were used to obtain different depths/energies. Nominal energy indicates energy provided as an option in the delivery system; actual energy, average energy at the exit of the nozzle obtained with a validated Monte Carlo model of the nozzle; range, actual range; depth, water equivalent depth in which FNTD was exposed; energy at depth, average energy at the specified depth obtained with a validated Monte Carlo model of the nozzle; and Φ-LET, fluence average LET in water at the specified depth.

Nominal energy (MeV)	Actual energy (MeV)	Range (cm)	Depth (cm)	Energy at depth (MeV)	Φ-LET H2O (keV/μm)
250	207.5	28.5	0.0	—	0.47
160	133.0	13.0	0.0	—	0.62
100	73.5	4.3	0.0	—	0.95
100	73.5	4.3	3.0	40.5	1.49
160	133.0	13.0	12.5	24.7	2.28

2.C. Readouts

FNTD chips were imaged with a commercial FCLSM system (FluoView 1200/IX-83, Olympus America, Inc., Center Valley, PA), which was custom-designed with a high-power red laser (641 nm, 80 mW) as one of the excitation sources. All readouts were performed at maximum laser power, which provides 7.5 mW at the focal plane of a 10× objective lens (UPLSAPO10X2, NA 0.4, Olympus America, Inc.). This 10× objective lens was used only to measure the laser power, and all laser powers in this work are quoted in terms of the 10× objective lens. The fluorescence signal was collected by a photomultiplier tube with a 670 nm long-pass emission filter. An oil immersion objective lens (UPLSAPO60XO, NA 1.35, Olympus America, Inc.) was used throughout to acquire images with high spatial resolution. The photomultiplier tube counts registered in each pixel were normalized to 12-bit grayscale.

To correlate track amplitudes with LET, 16 stacks of 20 depths through 80 μm (4 μm/slice) were collected for each FNTD chip (four chips per irradiation condition). Stacks were close to each other to minimize sensitivity changes and field of view correction.⁹ To quantify proton track amplitudes and correlate them with LET requires ensuring that pixels (12-bit depth) do not saturate. Thus, the imaging parameters must be selected such that track amplitudes from low- and high-LET proton tracks are within the 12-bit window. Imaging parameters were as follows: 512 × 512 pixels (52.7 μm × 52.7 μm), 641 nm laser, 105 μm diameter pinhole, 100 μs dwell time, 2× Kalman frame averages, 405/473/543/635 dichroic, photomultiplier tube voltage set to 700 V, 0% offset, and 1× gain.

The local ionization densities produced by delta rays are in general much lower than those produced by low energy proton tracks. Together, the ionization densities of protons and delta rays cause fluorescent signals, which span a range that is larger than the bit depth of our confocal system (12 bits) for the imaging parameters used to measure LET. Thus, to be able to visualize both delta rays and proton tracks, the imaging parameters need to be adjusted to increase the contrast in the low-fluorescent signal region, making the high-fluorescence signal in the core of the proton tracks saturate the pixel depth. The following imaging parameters were used to visualize both delta rays and proton tracks: 640 × 640 pixels (52.4 μm × 52.4 μm), 641 nm laser, 200 μm diameter pinhole, either 100 or 40 μs dwell time, 15× Kalman line averages, 405/473/543/635 dichroic, photomultiplier tube voltage set to 710 V, 0% offset and 1× gain.

2.D. Data analysis

To quantify track amplitudes in the FNTD chips, we used an image processing program developed in-house with LabView (National Instruments, Austin, TX). The algorithm uses 2D autocorrelation with a rotationally symmetric 2D Gaussian function (based on the optical resolution) to detect the track signal.

A threshold between detection noise and maximum pixel value is set manually to segment tracks and determine spot centroids. Briefly, the raw data are correlated with a rotationally symmetric 2D Gaussian function template with a full width of half maximum (FWHM) that is about the size of a primary track that traversed perpendicular to the image plane. Features in the image that correlate well with a primary proton track are amplified and those that do not are suppressed; this is autocorrelation. To detect track regions of interest, a threshold is applied to the correlated image. Because of intra- and inter-FNTD variations in coloration, we use a relative threshold cutoff based on individual image data, as opposed to an absolute 12-bit gray level, such that a single input could be used for an arbitrary image. We define the factor R = (A − C)/(B − C), where B is the threshold level, C is the noise floor, which is equal to the mean of all pixels in the autocorrelated image, and A is the maximum pixel value in the autocorrelated image, which corresponds to the amplitude of the maximally correlated track. Because autocorrelation is a linear operator, the track amplitude is a scaling factor such that the maximally correlated track is almost always the brightest (i.e., highest-LET) track. Then a factor R = 1.6 was manually determined based on tracks from an FNTD irradiated with 160 MeV at d = 12.5 cm. The factor R = 1.6 was used for all irradiation conditions and it was sufficient to obtain primary tracks without including too many delta rays, except for the lowest-LET condition (160 MeV, d = 0 cm) in which the threshold B was comparable to the amplitude of delta rays.

2D Gaussian functions are fit to the image data at the track locations by using the Levenberg–Marquardt nonlinear curve fit technique. The fit parameters are the amplitude, 2σ_x and 2σ_y, lateral shift, rotation, and offset of each track.

To account for depth-dependent optical aberrations and variations in FNTD sensitivity with depth, track amplitudes were calculated as the average amplitude over at least 17 depths in each image stack. We considered only tracks with angular incidence smaller than 6° relative to the FNTD surface plane to avoid intensity loss from angular dependence of the track spot amplitude.⁹ Track amplitude histograms were binned in 100 channels over all available track amplitude values. Corrections for spherical aberration and field of view nonuniformity⁹ were negligible and not applied.

Gaussian functions were fit to the track amplitude histograms that were obtained for each irradiation condition. The amplitude of the Gaussian function was used to normalize the respective LET spectrum, which was obtained with Monte Carlo simulations (described in Sec. 2.E).

3D images of the tracks in the FNTD volume were reconstructed with imaris image processing and analysis software (Bitplane AG, Zurich, Switzerland) for visualization.

2.E. Monte Carlo simulations

Monte Carlo simulations were done for the experimental conditions (Table I) in which the FNTDs were irradiated by using a validated Monte Carlo model of the beam line¹⁰ created in topas v1.3,¹¹ which is based on the geant 4 simulation toolkit.¹² We used the Monte Carlo model to obtain energy spectra for each irradiation condition (Table I). Simulations were done with the medium snout at 5 cm from isocenter, source to surface distance setup, 18 cm  × 18 cm field size, and unmodulated beams. A water volume of dimensions 30 cm × 30 cm × 32 cm was placed with its surface at isocenter. LET was calculated at the central axis at the surface or inside the water volume in a 5 cm × 5 cm × 0.5 mm volume by first scoring the energy spectrum of protons at the FNTD position under each irradiation condition. After simulation, the energy spectra were converted to LET spectra by means of a lookup table.¹³ All protons, both primary and secondary, were included in the scoring. Although all particles were transported including neutrons and particles with Z > 1, only protons (primary and secondary) were included in the scoring. Secondaries other than protons were not scored. The contribution of particles with Z > 1 to the total fluence is minor for the energies used in proton therapy.¹⁴ The production threshold for protons was set to 0.05 mm, and the thresholds for all other secondaries (including neutrons and particles with Z > 1) were set to the topas default of 0.05 mm with the exception of electrons. Electrons were not explicitly produced and tracked (production threshold set to 100 mm), as their inclusion has been found to slow simulations by a factor of ∼3 while having minimal effects on the resulting LET values.¹⁵ Secondary particle production thresholds for protons and electrons have been shown elsewhere to have minimal effects on resulting LET values.¹⁵

3. RESULTS

3.A. Visualization of individual proton tracks and delta rays

Proton tracks in FNTD chips exposed with their surfaces parallel or perpendicular to a high-energy unmodulated proton therapy beam (0.47 keV/μm) are shown in Figs. 1(A) and 1(B). White, red, and yellow arrows indicate examples of primary protons, secondary protons, and delta rays. Primary and secondary proton tracks have straight trajectories. Secondary proton tracks have large angles in respect to the direction of the beam. Delta rays have curved trajectories. These panels demonstrate that FNTDs are sufficiently sensitive to visualize proton tracks with LET as low as 0.47 keV/μm with nanoscale resolution. Secondary protons produced by the primary proton tracks are also visible.

FIG. 1.

Fluorescent images obtained after exposure to proton beams (0.47 keV/μm). (A) FNTD surface parallel to the beam. Image is maximum intensity projection (MIP) of 18 slices in 0.72-μm steps. (B) FNTD surface perpendicular to the beam, MIP of 30 slices in 0.5-μm steps. (C) 3D reconstruction of (B). Colors in (A) and (B) indicate the fluorescence amplitude in a 12-bits scale, which increases from blue to red. Arrows indicate examples of primary (white) and secondary (red) proton tracks, and delta rays (yellow). (See color online version.)

The 3D reconstruction of proton tracks through the FNTD (which allows the angular incidence of the tracks to be determined relative to the surface of the FNTD) is shown in Fig. 1(C). The 3D reconstruction is especially valuable for experiments in which cells are plated on the surface of the FNTD. The tracks in the FNTD can be extrapolated to the surface and to the position of subcellular compartments, thereby allowing determination of the trajectory of the track through the subcellular compartments.

3.B. LET of individual proton tracks

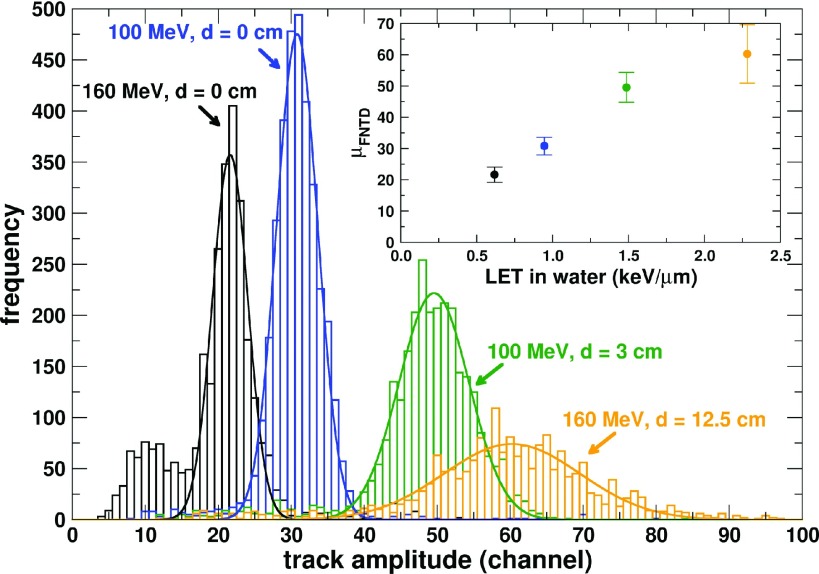
We next exploited the dependence of FNTD track amplitude on LET to develop a method to determine the LET of individual proton tracks. Track amplitude histograms from FNTD chips exposed to the conditions in Table I are shown in Fig. 2. As shown in the inlay of Fig. 2, the track amplitude clearly depends on the LET of proton therapy beams. The small peak at around channel 10 for the 160 MeV (d = 0 cm) is from delta rays. This delta ray peak appears only in the lowest-LET conditions (160 MeV, d = 0 cm) because only in this case is the threshold used in the track-finding algorithm close enough to background to include delta rays.

FIG. 2.

Track amplitude histograms (bars) obtained from FNTD chips exposed to the indicated conditions. The solid lines are Gaussian fits. Frequency is the number of tracks per channel. The inlay shows the peak position μ_FNTD of the Gaussian fits as a function of the fluence average LET of each condition (Table I). The error bars in the inlay represents the standard deviation of the Gaussian fit.

We used linear functions to map the FNTD track amplitude histograms to the respective LET spectrum for each condition,

$${\displaystyle \text{LET}=\frac{\text{FW}1{0\%}_{\text{LET}}}{\text{FW}1{0\%}_{\text{FNTD}}}\times \left(\text{ch}-{\mu }_{\text{FNTD}}\right)+{\mu }_{\text{LET}},}$$ (1)

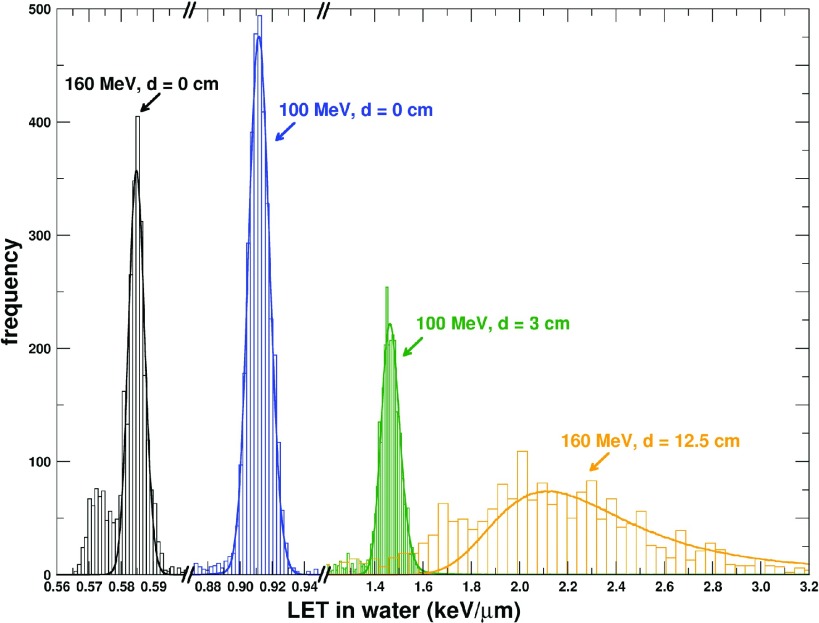
where ch is the channel, FW10%_LET and FW10%_FNTD are the full widths at 10% of the maximum of the LET spectrum and track amplitude histogram, respectively, and μ_LET and μ_FNTD are the peak positions of the LET spectrum and track amplitude histogram, respectively. Table II lists the parameters from Eq. (1) for each irradiation condition. Track amplitude histograms (bars) mapped to the respective LET spectrum for each condition are shown in Fig. 3. The solid lines represent the LET spectra for each irradiation condition.

TABLE II.

List of parameters from the LET spectra and Gaussian function fits to the track amplitude histograms. Φ-LET H₂O, fluence average LET in water at the position of the detector; μ_LET, peak position of the LET spectrum; FW10%_LET, full width at 10% of the maximum of the LET spectrum; A, amplitude of the track amplitude histogram; μ_FNTD, peak position extracted from the Gaussian fit of the track amplitude histogram; σ_FNTD standard deviation extracted from the Gaussian fit of the track amplitude histogram; and FW10%_FNTD, full width at 10% of the maximum extracted from the Gaussian fit of the track amplitude histogram.

Φ-LET H2O (keV/μm)	μLET (keV/μm)	FW10%LET (keV/μm)	A	μFNTD	σFNTD	FW10%FNTD
0.62	0.585	0.011	363	21.6	2.42	10.0
0.95	0.912	0.028	475	30.8	2.82	12.1
1.49	1.463	0.165	221	49.6	4.78	20.5
2.28	2.104	1.646	74	60.2	9.35	40.1

FIG. 3.

Track amplitude histograms (bars) mapped to the respective LET spectrum for each irradiation condition. The solid lines are the calculated LET spectra for each irradiation condition. Linear functions [Eq. (1)] based on the parameters of Table II were used to map the track amplitude histograms to the respective LET spectrum. The peak of each LET spectrum was scaled to the peak of the respective track amplitude histogram.

These results indicate further that FNTD track amplitude correlates with the LET of proton beams. Using the mapped linear functions for each irradiation condition allows the LET spectra to be related directly to the experimental conditions, which in turn indicates that the LET of individual proton tracks may be determined.

4. DISCUSSION

Previous studies have shown correlations between FNTD track amplitudes and ion effective charge and energy.^1,9,16,17 Our findings demonstrate that track amplitude of FNTDs can be directly linked to proton-LET, as suggested previously.¹⁸ Our findings also demonstrate that FNTDs are sufficiently sensitive to visualize tracks with LET values as low as 0.47 keV/μm. However, quantifying the track amplitude of low-LET proton beams is difficult because the LET spectrum of delta rays overlaps with the LET spectrum of the primary beam. Indeed, Figs. 2 and 3 show that track amplitudes of delta rays are comparable to the track amplitudes of the primary protons for LET lower than approximately 0.6 keV/μm.

In mapping the track amplitude histograms to their respective LET spectra (Fig. 3) by using Eq. (1), the spectral width FW10%_LET was found to depend nonlinearly on FW10%_FNTD, which implies that a single linear scaling factor between LET and track amplitude cannot be determined with this technique for all irradiation conditions simultaneously. This suggests a limitation of the method presented in this work to define a general batch calibration of the FNTDs. Nevertheless, for irradiation conditions in which LET spectra data are available, our data indicate the potential to spatially map the LET of individual tracks within a particular experimental condition. However, further studies are necessary to determine the LET resolution of the FNTDs.

This study fundamentally differs from our work on simultaneous measurements of average LET and absorbed doses at the macroscopic level using Al₂O₃:C optically stimulated luminescence detectors (OSLDs)^10,19,20 in that this work focuses on LET measurements of single proton tracks. In this work, our aim was to spatially map the LET spectrum to a specific experimental condition. Such measurements have applications in radiobiology experiments in which cells are cultured on the surface of the FNTDs.^4,5 Our aim in our previous work^10,19,20 was to provide an easy-to-use method to measure both LET and absorbed dose in patient-specific fields for the purpose of quality assurance of LET-optimized treatment plans.

The accuracy of individual track LET calibration is limited by the nonuniformity of color centers within the same FNTD chip and between different FNTD chips, which can introduce significant uncertainties (up to 10%) in fluorescence track amplitudes.⁹ For this study, we used preselected FNTD chips to minimize differences in chip-to-chip sensitivity variations, which allowed us to distinguish the FNTD response to each irradiation condition. The same method presented here can be used with a single FNTD chip to eliminate chip-to-chip nonuniformity of color centers.

FNTDs have been used to measure proton, carbon, and neon ion tracks^9,18,21,22 and to visualize delta rays from a carbon ion beam. Here we show that FNTDs can also image delta rays created by therapeutic proton beams and the track structure within individual proton tracks.

The FNTD technology has become a useful tool for radiobiology studies because it allows spatial correlation between the trajectory of tracks and cellular response.^4–7,23 The results presented here also allow LET to be incorporated into analyses of biological experiments in which FNTDs are used as substrates.^4,5,23 The described techniques will allow the biological response to be linked not only to the path of the track but also to the LET of the track. This will potentially enable investigations at the single-cell level on the effect of LET in the DNA damage response, consequently leading to a better understanding of relative biological effectiveness.

Our technique provides nanoscale spatial resolution of tracks, which are limited by diffraction (lateral resolution of ∼280 nm).²⁴ This resolution is required to spatially correlate tracks with radiation-induced single- and double-strand break foci, which may be visualized in fluorescent-tagged cells. These foci are smaller than the point spread function of conventional confocal systems.

The technique presented here to determine the LET of individual proton tracks could also be applicable to carbon ion beams in which particle and LET spectra are complex. In the context of radiobiology experiments, the LET spectrum from a carbon ion beam contains a large fraction of nuclear fragments with a large range of LET values that differentially affect the biological response more than protons.

5. CONCLUSIONS

We demonstrated that FNTDs provide nanoscale spatial resolution and sufficient sensitivity to allow imaging of individual proton tracks and delta rays from proton therapy beams. FNTDs further have the potential to measure LET of individual proton tracks from proton therapy beams.