Importance of ocean salinity for climate and habitability

Significance

The habitability of the growing number of confirmed exoplanets is a question of wide interest and importance. A key factor determining habitability is planetary climate, which is influenced heavily by the presence of liquid water oceans, and in particular, the heat transported around the planet by these oceans. Here the impact of average ocean salinity, a key property in determining the density of water, on ocean state is investigated. It is shown that oceans that have sufficiently different average salinities to Earth consist of circulations of opposite direction: sinking in the tropics, filling the deep ocean with warm water, and ultimately warming the polar regions. Variations in ocean properties can therefore extend the range of exoplanet habitability.

Abstract

Modeling studies of terrestrial extrasolar planetary climates are now including the effects of ocean circulation due to a recognition of the importance of oceans for climate; indeed, the peak equator-pole ocean heat transport on Earth peaks at almost half that of the atmosphere. However, such studies have made the assumption that fundamental oceanic properties, such as salinity, temperature, and depth, are similar to Earth. This assumption results in Earth-like circulations: a meridional overturning with warm water moving poleward at the surface, being cooled, sinking at high latitudes, and traveling equatorward at depth. Here it is shown that an exoplanetary ocean with a different salinity can circulate in the opposite direction: an equatorward flow of polar water at the surface, sinking in the tropics, and filling the deep ocean with warm water. This alternative flow regime results in a dramatic warming in the polar regions, demonstrated here using both a conceptual model and an ocean general circulation model. These results highlight the importance of ocean salinity for exoplanetary climate and consequent habitability and the need for its consideration in future studies.

With the ongoing discovery of exoplanets, it is natural to question their habitability. The most widely accepted definition of a habitable planet is one that can sustain liquid water on its surface (1), which usually implies a range of orbital radii in which a planet receives a level of stellar radiation that enables surface liquid water to be sustained (2, 3). Habitability and climate also depend on heat being transported effectively around the planet, which is achieved through the circulation of the atmosphere and ocean. There are many studies describing simulations of exoplanetary atmospheric circulations and climate (4), but most incorporate either no ocean (5–7) or a heavily simplified slab ocean (8–12). Only recently have studies considered a dynamical ocean (13–16), and even in these studies, the ocean is consistently assumed to have similar properties to the oceans on Earth. Such an assumption may prove to be an oversimplification. More recently changes in ocean properties have begun to be investigated, for example, ocean depth (17), and here, salinity, which has significant influence on density.

There is evidence on Earth that the mean ocean salinity has decreased from up to double the present day level since the Archean (18, 19). In addition, modeling of water delivery during planetary formation concludes that there could be an extensive range of possible ocean masses (20, 21). Planets in the habitable zone may have oceans with a small fraction to hundreds of times the volume of the oceans on Earth, which will have important implications for the geological evolution of the planet and the salinity of any oceans. Ocean salinity can also be influenced by planetary properties, for example, the immense pressures at the floor of a very deep ocean could maintain a layer of ice at the bottom of the ocean. This scenario would limit any geological processes that increase salinity and hence maintain an ocean with a low salinity (3).

Here the impact of mean ocean salinity is investigated with a well-known conceptual two-box model for ocean circulation, as well as a more complex 3D ocean general circulation model (OGCM), allowing comparison with the conceptual model. Three specific salinity ranges, which span the range found on Earth, will be considered in this study: low, mid-, and high, which have typical salinity values of 0 (freshwater), 35 (Earth ocean), and 260 g⋅kg⁻¹ (Dead Sea), respectively. The equation of state is an empirical relationship linking temperature, salinity, pressure, and density, which means a separate experimental study is needed to obtain it for each of the salinity ranges. Each equation is only valid within the ranges of temperature, salinity, and pressure for which the water mass is examined in the study in which it is devised. The resulting discontinuity prevents any continuous investigation across a large range of salinity values. In each case, an appropriate approximation is made to the full equation of state to obtain an exact solution for the box model (Materials and Methods). The approximated equations of state are also used in the OGCM to allow for the closest comparison with the conceptual model.

For the low salinity scenario, the equation of state is a nonmonotonic function of temperature, approximated by a quadratic relation between temperature and density. This behavior is apparent for salinity up to 27.4 g⋅kg⁻¹, although the temperature range over which the nonmonotonic behavior occurs narrows as salinity is increased toward this limit (22). For the mid- and high salinity scenarios, the density increases monotonically with decreasing temperature and increasing salinity in such a way that a linear approximation of the equation of state is appropriate. To determine an analytic solution to the box model in the low salinity range, the freshwater case is considered, and in the mid- and high ranges, analytic solutions are obtained by reducing the problem to depend on the gradients in temperature and salinity forcing. It is important to note that the salinity gradient is approximately proportional to the mean salinity (Materials and Methods). This relationship means that the same value of freshwater input into a water mass of a higher salinity will result in a larger absolute change in salinity. For both models, the impact of freshwater exchange is represented by a salt flux.

Results

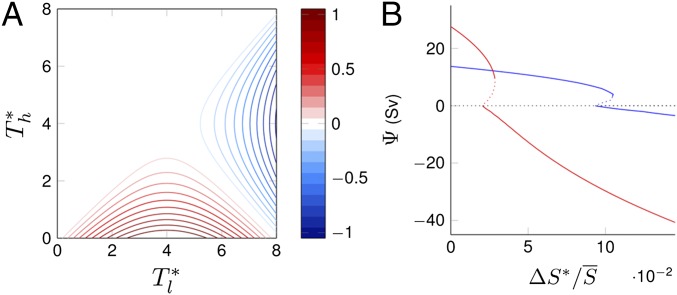
The solutions to the Stommel box model (23) determine whether a particular climate configuration results in a circulation that has poleward traveling surface water (positive circulation) or equatorward traveling surface water (negative circulation) (Materials and Methods). Fig. 1A shows how the circulation varies in the freshwater scenario as the temperature forcing of each box varies. Surface temperatures are forced to values in the range 0–8 °C, chosen because the maximum density occurs at 4 °C and the freezing point is 0 °C. Due to the nonlinear behavior of the equation of state, the circulation is negative when the temperature of the low latitude box is closer to 4 °C than the high latitude box: a behavior that is qualitatively different from the other scenarios considered. Fig 1B shows the direction of the circulation in the mid- and high cases, with the temperature forcing held constant and the effect of varying the salinity forcing assessed. The results show a positive circulation with a low gradient in salinity forcing, multiple solutions with a moderate gradient, and a reversal of the circulation to a negative, salinity-driven regime at higher salinity gradients (23). Outside of the multiple solution range, the model results show that a gradient in the salinity forcing of 3.5 and 8 g⋅kg⁻¹ in the mid- and high case, respectively, results in a salinity-driven circulation. This difference corresponds to a relative forcing of magnitude five times smaller for a salinity-driven circulation in the high salinity case compared with the midrange case. Note that, although larger in absolute value, the value of salinity forcing in the high salinity case is relatively weaker due to the proportionality between the mean salinity and the salinity gradient. Thus, in the high range salinity scenario it is more likely that a negative circulation occurs, with sinking at the equator, and warm water traveling poleward at depth: opposite to what is seen on Earth. The simplifications in the box model limit the quantitative applicability of the conclusions that may be drawn; however, it does provide a useful summary of the general qualitative behavior of the system.

Fig. 1.

Box model solutions for the magnitude of the overturning circulation $\mathrm{\Psi }$ (Sv = 10⁶ m³⋅s⁻¹) for the three salinity scenarios. (A) Freshwater case with surface temperature forcing $T_h^{\text{∗}}$ and $T_l^{\text{∗}}$ (°C), of the high and low latitude box, respectively, in the range 0–8 °C, contour interval 0.1 Sv. Positive circulation occurs when $T_h^{\text{∗}}<T_l^{\text{∗}}<8-T_h^{\text{∗}}$ (assuming $T_h^{\text{∗}}<T_l^{\text{∗}}$). (B) Mid- (blue) and high (red) range salinity scenarios, dotted lines indicate unstable solutions, $\mathrm{\Delta }{S}^{\text{*}}$ is the gradient in salinity forcing, and $\overline{S}$ is the mean salinity. The scaling $\mathrm{\Delta }{S}^{\text{*}}\propto \overline{S}$ means direct comparison is possible when $\mathrm{\Delta }{S}^{\text{*}}/\overline{S}$ is varied. The range presented is equivalent to 0–5 and 0–38 g⋅kg⁻¹ for $\mathrm{\Delta }{S}^{\text{*}}$ in the midrange and high range salinity cases, respectively. A salinity-driven circulation occurs when $\mathrm{\Delta }{S}^{\text{*}}/\overline{S}>$ 0.105 and 0.03, respectively.

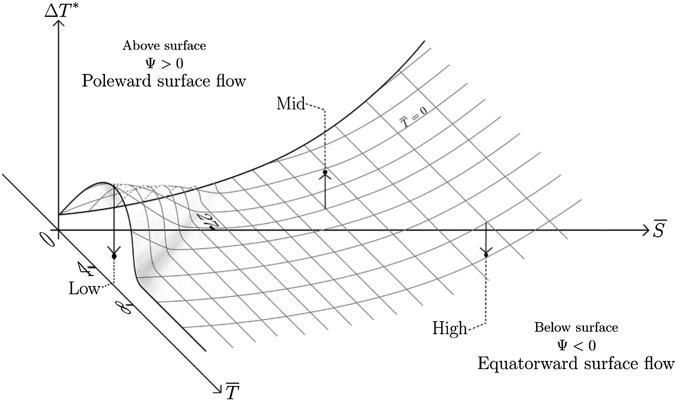
The results presented above can be concisely summarized using a regime diagram to illustrate circulation direction as a function of three variables: mean temperature, equator-pole temperature gradient, and equator-pole salinity gradient (Fig. 2). The gridded surface represents the values where there is no circulation, above the surface there is a positive circulation (poleward flowing surface water), and below it there is a negative circulation (equatorward flowing surface water). The magnitude of the circulation is strengthened as the distance (and hence density difference between the boxes) from the surface increases. The figure illustrates how a negative circulation becomes increasingly likely as the mean salinity increases, indicated by the surface tilting upward with an increasing salinity gradient. The key factor is the balance between the temperature and salinity forcing, because they act in opposing directions. For example, a negative salinity-driven circulation occurs at a midrange salinity if the temperature gradients are sufficiently small (below the surface in Fig. 2). An example of this occurring could be on a planet whose atmosphere is considerably denser than that of Earth, which results in a significantly smaller equator-pole temperature gradient (8, 24). This idea has featured in attempts to explain the evidence for the presence of warm deep water in the Cretaceous, hypothesized to be the result of significantly higher evaporation rates rather than a higher mean salinity (25).

Fig. 2.

A schematic illustrating the direction and magnitude of the overturning circulation, $\mathrm{\Psi }$, from the box model solutions. The behavior depends on the values of temperature gradient forcing $\mathrm{\Delta }{T}^{\text{*}}$, the mean temperature $\overline{T}$, and mean salinity $\overline{S}$. The proportionality between the salinity gradient forcing $\mathrm{\Delta }{S}^{\text{*}}$ and $\overline{S}$ means the two values do not need separate consideration, whereas $\mathrm{\Delta }{T}^{\text{*}}$ and $\overline{T}$ can be varied independently. Note the lower limit of $\overline{T}$ decreases as $\overline{S}$ increases and lowers the freezing point. Values lying on the surface have zero circulation $\mathrm{\Psi }=0$; those above and below have positive and negative circulation, respectively, with increasing magnitude with increasing distance from the surface. The values defining the low-salinity, low-temperature range are indicated; 0–8 °C and 0–27 g⋅kg⁻¹, with the local maximum at $\overline{T}=$ 4 °C, $\overline{S}=$ 0 g⋅kg⁻¹. The locations of the low, mid-, and high salinity ranges considered in this study are indicated in reference to the surface. The curvature of the surface results from the nonlinear dependence of density on temperature and salinity.

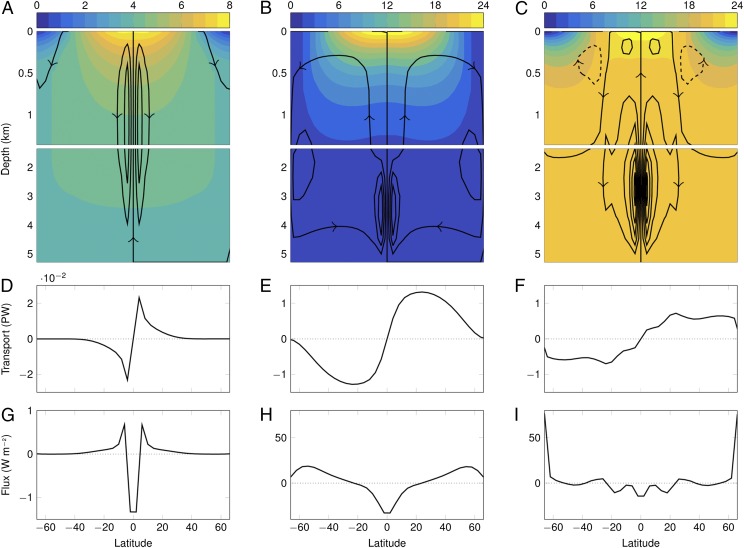
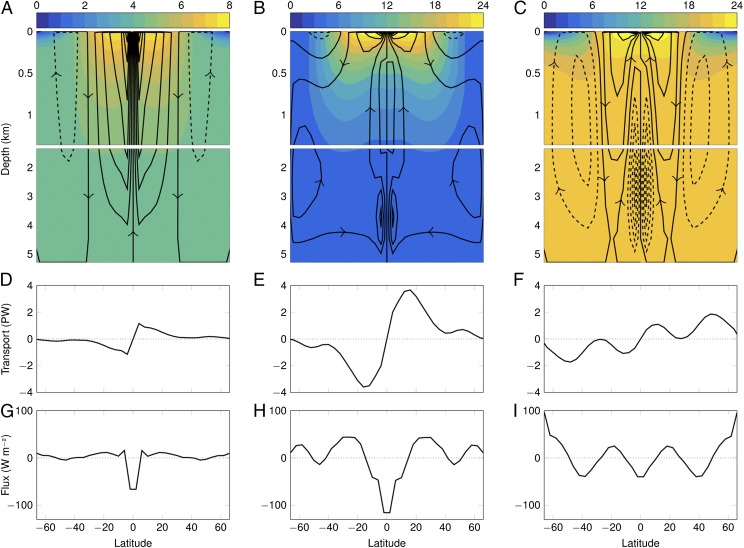
The same three salinity scenarios are also investigated using an OGCM, in this case, the Modular Ocean Model–Array Processor Version (MOMA) (26, 27), applying the same approximate equations of state as used for the box model. The structure of the circulation in each of the three cases is shown by the contours of the overturning streamfunction in Fig. 3 A–C. Each streamline follows the zonally averaged flow of water and hence indicates the locations of deep water formation and upwelling by locating the latitudes at which the contours descend away from or ascend toward the surface, respectively. The results presented for a freshwater ocean have a surface forcing in the range 0–8 °C to show the structure of the circulation more clearly. Fig. 3A shows that deep water forms in the region of 45°N/S, which corresponds to the 4 °C contour in the zonally averaged temperature, which is the temperature at which water density is greatest. This location of deep water formation creates two overturning cells in each hemisphere that circulate in opposite directions. The largest transport occurs in the cell that is closer to the equator, which restricts the vast majority of the ocean heat transport to the lower latitudes. The poleward heat transport peak of 0.023 PetaWatts (PW = 10¹⁵ W) occurs at 4°N/S (Fig. 3D), which corresponds to the latitude of the maximum surface heat flux to the atmosphere of 0.7 W⋅m⁻² (Fig. 3G). The mass and heat transport across the 4 °C contour is negligible. Although small, the surface heat flux poleward of the deep water formation region is into the ocean because of cold water traveling equatorward at the surface. As expected, the midrange salinity scenario has the general behavior of that observed on Earth; one temperature-driven cell in each hemisphere with deep water formation at the poles and upwelling at the equator (Fig. 3B). This circulation transports warm equatorial surface water to the higher latitudes where the transported heat is given up to the atmosphere (Fig. 3H). The peak heat transport of 1.3 PW occurs in the region of 20°N/S (Fig. 3E).

Fig. 3.

Plots showing the results from the OGCM for the freshwater (A, D, and G), mid- (B, E, and H), and high (C, F, and I) range salinity scenarios; note the different scales in A, D, and G. (A–C) Black contours of the overturning streamfunction $\mathrm{\Psi }$ show the structure of the meridional overturning circulation through the depth of the ocean. The contour intervals are (A) 1 Sv (=10⁶ m³⋅s⁻¹) and (B and C) 20 Sv. Solid and dashed contours indicate positive (poleward surface flow) and negative (equatorward surface flow) circulation, respectively, as indicated by the arrows. Note the different depth scales; the surface layer is extended to show this region of finer detail; the color shading in A–C shows the zonally averaged temperature (°C). (D–F) Northward ocean heat transport (PW = 10¹⁵ W). (G–I) Surface heat flux (W⋅m⁻²); positive values are from ocean to atmosphere.

In the high salinity scenario, the configuration of the cells is similar to those in the low salinity case: four cells of negative and positive direction in the high and low latitudes, respectively (Fig. 3C). In this case, the lower latitude cells extend down into the deep ocean, whereas those poleward of this are much shallower. The location of deep water formation is at 20°N/S, forming the boundary between the two cells within each hemisphere and is the latitude that is forced to the greatest surface density (Fig. S1C). The poleward heat transport peaks near 20°N/S at 0.7 PW with another local peak at 50°N/S. The deep ocean is filled with warm and saline water due to the location of deep water formation occurring at such a low latitude. The upwelling at high latitudes from the negatively circulating cell brings this warm deep water to the surface, giving the peak surface heat flux of 80 W⋅m⁻² (Fig. 3I), over twice the magnitude of the peak surface heat flux in the midrange salinity case. Water surfaces at the highest latitudes and rapidly exchange heat with the atmosphere; this cooled water then travels equatorward at the ocean surface, resulting in a heat flux into the ocean between 50 and 40°N/S. In this regime, the ocean carries heat to the polar regions through the deep ocean, which is fundamentally different to the circulation of the oceans on Earth where heat is transported poleward at the surface.

Fig. S1.

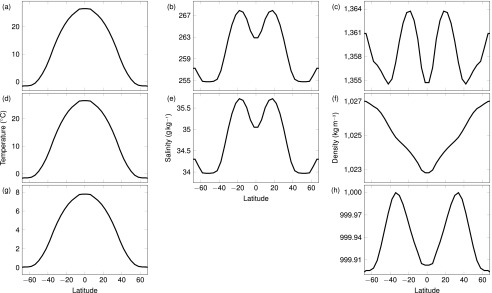
Plots showing the zonally averaged profiles of atmospheric temperature (A, D, and G) and salinity (B and E) forcing on the surface of the ocean in the OGCM, for the high (A–C) and mid- (D–F) range salinity scenarios, and the freshwater case (G and H). Note there is no salinity forcing in the freshwater case. The density forcing (C, F, and H) is calculated from the temperature and salinity values shown using the relevant equation of state.

Alongside buoyancy forcing, surface wind stress on the ocean may also have significant influence on the large-scale ocean circulation and resulting heat transport. This influence is investigated using the OGCM in the same configuration for each salinity range but with the inclusion of wind forcing (Fig. 4). The most notable influence of wind forcing is in the freshwater scenario (Fig. 4 A, D, and G); the strength of the overturning is significantly increased, resulting in a peak ocean heat transport more than an order of magnitude larger. The small density differences, and thus weak buoyancy-driven overturning, in this scenario mean that wind forcing has a large impact on the magnitude of the circulation. In the mid- and high salinity cases, wind forcing approximately doubles the peak ocean heat transport (Fig. 4 E and F). In both the freshwater and high salinity scenarios, a deepening and relative strengthening of the higher latitude cell is observed (Fig. 4 A and C), increasing the magnitude of the heat transport in these regions (Fig. 4 D and F), and in the high salinity case locating the peak ocean heat transport in this cell.

Fig. 4.

Plots showing the results from the OGCM for the freshwater (A, D, and G), mid- (B, E, and H), and high (C, F, and I) range salinity scenarios with the inclusion of wind forcing. (A–C) Black contours of the overturning streamfunction $\mathrm{\Psi }$ show the structure of the meridional overturning circulation through the depth of the ocean; the contour interval is 20 Sv (=10⁶ m³⋅s⁻¹). Solid and dashed contours indicate positive (poleward surface flow) and negative (equatorward surface flow) circulation, respectively, as indicated by the arrows. Note the different depth scales; the surface layer is extended to show this region of finer detail. The color shading in A–C shows the zonally averaged temperature (°C); note the different scale in A. (D–F) Northward ocean heat transport (PW = 10¹⁵ W). (G–I) Surface heat flux (W⋅m⁻²); positive values are from ocean to atmosphere.

Discussion and Conclusion

An ocean where the temperature gradient is the dominating driver of circulation typically exhibits sinking at the poles, with the exception of when the orbital obliquity is so high that the poles receive more solar radiation than the equator (28). However, in a scenario such as the high case presented here, the circulation is driven primarily by the gradient in salinity. As ocean salinity increases, the density responds far more strongly to differences in precipitation and evaporation; hence, the circulation has much stronger dependence on the salinity forcing. This profile of salinity forcing varies significantly with the degree of obliquity, and consequently, the circulation also exhibits this strong dependence. For instance, in the present work, the OGCM is forced by zonally averaged temperature and salinity profiles derived from observations on Earth, which includes the effects of the seasonally varying intertropical convergence zone (ITCZ). The greatest salinity forcing is at the edges of the ITCZ at ∼20°N/S, which defines this as the latitude of deep water formation in the high case (Fig. 3C). However, no such effect is seen in the midrange salinity scenario (Fig. 3B). Our results therefore suggest that the extent of the effect of orbital obliquity on planetary ocean circulation also depends on ocean salinity.

As the salinity of water increases, the freezing point decreases (29), meaning that an ocean of higher salinity has less potential to form sea ice and therefore remains ice free at much lower temperatures. As well as having direct impacts on the ocean circulation, this also results in less global ice coverage, lowering the planetary albedo and consequently warming the climate (30) and directly changing the width of the habitable zone.

Here the impact of global mean salinity on the large-scale circulation of the ocean has been investigated. On any given exoplanet, many other properties are likely to differ from their Earth-like values, some of which may also have significant influence on ocean circulation, such as tidal locking (13), planetary rotation period (14), ocean depth (17), obliquity (28), and continental configuration (31–33). The combined effect of these parameters, including ocean salinity, should be investigated in the future. In particular, the application of a higher-resolution eddy resolving ocean model to this problem is distinctly desirable, but computational constraints presently preclude such sensitivity studies.

The implications of the value of ocean salinity on climate were investigated for the first time to our knowledge and showed great significance for the entire structure of the large-scale ocean circulation and the resulting ocean heat transport. Indeed, the mean salinity of the ocean might be considered to be key in determining ocean thermal structure in an analogous manner to atmospheric pressure. It is therefore concluded that it is important to consider the likely variation of ocean salinity in the modeling of exoplanetary climate and when making conclusions about habitability.

Materials and Methods

For the low salinity scenario, the equation of state, for the density ${\rho }_f$, is approximated by the quadratic equation

$${\rho }_L={\rho }_0\left[1-{\alpha }_L^2{\left(T-\tilde{T}\right)}^2\right],$$

where T is temperature, $\tilde{T}$ (=4 °C for freshwater) is the temperature of the maximum density, ${\rho }_0=1,000$ kg⋅m⁻³ is a reference density, and ${\alpha }_L=2.3\times {10}^{-3}$ °C⁻¹ is the coefficient of thermal expansion (34). For the mid- and high salinity scenarios, a linearization of the equation of state takes the form

$${\rho }_r={\rho }_0\left(1-{\alpha }_{r}T+{\beta }_{r}S\right),$$

where S is salinity, and r represents either M or H for mid- and high range salinity, respectively. The values ${\alpha }_M=1.7\times {10}^{-4}$ °C⁻¹ and ${\beta }_M=7.8\times {10}^{-4}$ kg⋅g⁻¹, the coefficients of thermal expansion and haline contraction, respectively (22), are obtained through a Taylor expansion of the full equation of state for seawater. For the high range, ${\alpha }_H=5.0\times {10}^{-4}$ °C⁻¹ and ${\beta }_H=14.0\times {10}^{-4}$ kg⋅g⁻¹ are calculated by applying the same approach to the equation of state for Dead Sea water (35). The Stommel box model (23) consists of two connected boxes, one representing the high latitudes and the other the low latitudes, each containing water of uniform density. The density of the water in a box is determined by the temperature and salinity values to which it is forced, denoted $T_h^{\text{∗}},\hspace{0.5em}{T}_l^{\text{∗}},\hspace{0.5em}{S}_h^{\text{∗}},\hspace{0.5em}\text{and}\hspace{0.5em}{S}_l^{\text{∗}}$ for the temperature and salinity of the high and low latitude box, respectively. It is always assumed that the high latitude box is colder and fresher than that of the low latitudes; $T_h^{\text{∗}}\le T_l^{\text{∗}}$, $S_h^{\text{∗}}\le S_l^{\text{∗}}$. A circulation occurs due to the density gradient between the water in each box. The full time-dependent equations for the temperature and salinity in the high and low latitudes, respectively, and the overturning streamfunction $\mathrm{\Psi }$, are

$$\frac{d{T}_h}{dt}=c\left(T_h^{\text{∗}}-T_h\right)-\frac{2}{V}\left|\mathrm{\Psi }\right|\left(T_h-T_l\right),$$

$$\frac{d{T}_l}{dt}=c\left(T_l^{\text{∗}}-T_l\right)-\frac{2}{V}\left|\mathrm{\Psi }\right|\left(T_l-T_h\right),$$

$$\frac{d{S}_h}{dt}=d\left(S_h^{\text{∗}}-S_h\right)-\frac{2}{V}\left|\mathrm{\Psi }\right|\left(S_h-S_l\right),$$

$$\frac{d{S}_l}{dt}=d\left(S_l^{\text{∗}}-S_l\right)-\frac{2}{V}\left|\mathrm{\Psi }\right|\left(S_l-S_h\right),$$

$$\mathrm{\Psi }=A\left({\rho }_h-{\rho }_l\right),$$

where t is time, $c=6.4\times {10}^{-}8$ s⁻¹ and $d=2.1\times {10}^{-}8$ s⁻¹ are inverse timescales for temperature and salinity diffusion, respectively, $V={10}^{15}$ m³ is the volume of the boxes, ${\rho }_h\left(T_h,S_h\right)$ and ${\rho }_l\left(T_l,S_l\right)$ are densities of the respective boxes, and $A={10}^7{\text{m}}^6{\text{kg}}^{-1}{\text{s}}^{-1}$ is a constant of proportionality. Here, d/d$t\equiv 0$ is chosen to find the steady state solutions for the overturning streamfunction $\mathrm{\Psi }\left(T_h^{\text{∗}},T_l^{\text{∗}},S_h^{\text{∗}},S_l^{\text{∗}}\right)$. For the mid- and high range salinity scenarios, the linearized equation of state allows the above four equations for the box model to be simplified to two equations in terms of the gradients $\mathrm{\Delta }T=T_l-T_h$, $\mathrm{\Delta }S=S_l-S_h$, $\mathrm{\Delta }{T}^{\text{*}}=T_l^{\text{∗}}-T_h^{\text{∗}}$, and $\mathrm{\Delta }{S}^{\text{*}}=S_l^{\text{∗}}-S_h^{\text{∗}}$ to find $\mathrm{\Psi }\left(\mathrm{\Delta }{T}^{\text{*}},\mathrm{\Delta }{S}^{\text{*}}\right)$

$$c\left(\mathrm{\Delta }{T}^{\text{*}}-\mathrm{\Delta }T\right)-\frac{4}{V}\left|\mathrm{\Psi }\right|\mathrm{\Delta }T=0,$$

$$d\left(\mathrm{\Delta }{S}^{\text{*}}-\mathrm{\Delta }S\right)-\frac{4}{V}\left|\mathrm{\Psi }\right|\mathrm{\Delta }S=0,$$

$$\mathrm{\Psi }=A{\rho }_0\left({\alpha }_r\mathrm{\Delta }T-{\beta }_r\mathrm{\Delta }S\right).$$

The scaling $\mathrm{\Delta }S\propto \overline{S}$ is derived by considering the Stommel box model configured with mean salinity $\overline{S}$, overturning $\mathrm{\Psi }$, and atmospheric freshwater transport Q. The mean salinity $\overline{S}$ is chosen such that the two connected boxes have salinity $\overline{S}+s\prime$ and $\overline{S}-s\prime$, where $s\prime$ is the salinity anomaly, and so $\mathrm{\Delta }S=2s\prime$. Considering the change in salinity in one of the boxes, here chosen to be the low latitude box, due to the sum of the inward and outward flow, gives

$$\frac{d\left(\overline{S}+s\prime \right)}{dt}=\frac{1}{V}\left[\left(\overline{S}-s\prime \right)\mathrm{\Psi }-\left(\overline{S}+s\prime \right)\left(\mathrm{\Psi }-Q\right)\right].$$

Taking the steady state gives

$$\left(\mathrm{\Psi }-\frac{Q}{2}\right)\mathrm{\Delta }S=Q\overline{S},$$

$$\mathrm{\Delta }S\propto \overline{S},$$

for given $\mathrm{\Psi }$ and Q.

The OGCM used is MOMA (26, 27) configured at a horizontal resolution of 4° with 15 vertical levels ranging from 30 m at the surface to a maximum of 836 m at depth. The horizontal momentum viscosity is ${10}^5$ m²⋅s⁻¹, the vertical viscosity is ${10}^{-4}$ m²⋅s⁻¹, and the horizontal and vertical diffusivities are $5\times {10}^3$ and ${10}^{-4}$ m²⋅s⁻¹, respectively. An aquaplanet land configuration is used (14), which consists of a single full-depth meridional barrier connecting two polar islands that extend to 68°N/S. This arrangement is the simplest representation of any substantial land configuration (31). The model results presented are an average of the last 1,000 y of an 8,000-y run.

The atmospheric forcing of ocean temperature and salinity at the surface of the ocean in MOMA is incorporated by a relaxation of the surface ocean temperature and salinity to prescribed zonally averaged atmospheric profiles that are based on observed climatologies (36) (Fig. S1). Similarly, the surface momentum forcing is derived from an observed wind stress climatology (37). The surface forcing profiles are made symmetric about the equator by reflecting the southern hemisphere forcing, where on Earth there is a greater proportion of ocean, in the northern hemisphere. The forcing in each case is adapted to correspond to the appropriate range of salinity and temperature in that scenario; in the midrange case, the values remain unchanged from the Earth observations; in the freshwater case the temperature values are scaled to be in the range 0–8 °C and salinity is removed; and in the high case, the salinity values are scaled to be in the range 240–268 g⋅kg⁻¹ in accordance with the scaling $\mathrm{\Delta }S\propto \overline{S}$. In the high salinity case, the ocean is initialized at 21 °C, instead of the standard value 0 °C, as this is closer to the final steady state of the deep ocean and therefore negates an initial long period of vertical heat diffusion into the deep ocean, significantly reducing the spin-up period.