How computer simulations of the human heart can improve anti‐arrhythmia therapy

Abstract

Over the last decade, the state‐of‐the‐art in cardiac computational modelling has progressed rapidly. The electrophysiological function of the heart can now be simulated with a high degree of detail and accuracy, opening the doors for simulation‐guided approaches to anti‐arrhythmic drug development and patient‐specific therapeutic interventions. In this review, we outline the basic methodology for cardiac modelling, which has been developed and validated over decades of research. In addition, we present several recent examples of how computational models of the human heart have been used to address current clinical problems in cardiac electrophysiology. We will explore the use of simulations to improve anti‐arrhythmic pacing and defibrillation interventions; to predict optimal sites for clinical ablation procedures; and to aid in the understanding and selection of arrhythmia risk markers. Together, these studies illustrate how the tremendous advances in cardiac modelling are poised to revolutionize medical treatment and prevention of arrhythmia.

Abbreviations

AF

atrial fibrillation

APD

action potential duration

CHD

congenital heart disease

DFT

defibrillation threshold

DTI

diffusion tensor imaging

GZ

grey zone

ICD

implantable cardioverter defibrillator

LGE

late gadolinium enhancement

LV

left ventricle

MRI

magnetic resonance imaging

MTWA

microvolt T‐wave alternans

QT

ECG interval between ventricular depolarization and repolarization

SCD

sudden cardiac death

VF

ventricular fibrillation

V_m

transmembrane potential

VT

ventricular tachycardia

Introduction

Computer modelling of heart function has emerged as a powerful tool in the study of heart rhythm and pump disorders. Biophysically detailed cardiac simulations can explain experimental observations and help reveal how organ‐scale arrhythmogenic phenomena (ectopic heartbeats, conduction failure, electrical turbulence, etc.) and contractile dysfunction emerge from pathological effects at the tissue, cell and protein levels. This extensive ‘virtual heart’ methodology (Noble, 2002; Vigmond et al. 2009; Gurev et al. 2011; Trayanova, 2011, 2014; Winslow et al. 2012) has been built upon a strong foundation of experimentally constrained model developments. Advancements in single‐cell action potential modelling have produced the contemporary building blocks for constructing models of the atria (Courtemanche et al. 1998, 1999; Nygren et al. 1998; Maleckar et al. 2009; Grandi et al. 2011) and the ventricles (ten Tusscher & Panfilov, 2006; Fink et al. 2008; Grandi et al. 2010; O'Hara et al. 2011) with high levels of biophysical detail. Similarly, cell mechanics (myofilament) models (reviewed in Trayanova & Rice, 2011) have enabled the assembly of coupled electromechanical models of the heart. Such developments have helped to fuel the exciting progress made in simulating cardiac electrical (McDowell et al. 2011; Moreno et al. 2011; Relan et al. 2011; Tandri et al. 2011; Trayanova et al. 2012; Boyle et al. 2013, 2014; Clayton & Bishop, 2014; Trayanova & Boyle, 2014) and mechanical (Gurev et al. 2011, 2015; Nordsletten et al. 2011; Land et al. 2012; Hu et al. 2013 a,b, 2014; Krishnamurthy et al. 2013; Tobon‐Gomez et al. 2013; Fritz et al. 2014; Lim et al. 2015) behaviour at the organ level. Importantly, the emergent, integrative behaviours in the heart uncovered by these modelling studies have demonstrated how they result from complex interactions not only within a specific structural level but also from feed‐forward and feedback interactions that connect a broad range of hierarchical levels of biological organization, further underscoring the importance of integrative research in heart (dys)function. Several recent reviews have been written on our current understanding of the mechanisms of atrial and ventricular mechanisms from an integrative interactions perspective (Janse, 2004; Rubart & Zipes, 2005; Jacquemet et al. 2008; Plank et al. 2008; Rudy et al. 2008; Fishman et al. 2010; Dossel et al. 2012; John et al. 2012; Trayanova, 2012, 2014; Chen et al. 2014; Heijman et al. 2014), often derived from computer simulations.

In the modelling of heart rhythm disorders, recent developments have begun to focus extensively on clinically driven problems (Narayan et al. 2008; Bayer et al. 2010; Krummen et al. 2012) or to adopt the patient‐specific approach (Gurev et al. 2011; Ashikaga et al. 2013; Prakosa et al. 2014), where the geometry and structure of the heart (including structural remodelling such as infarction (Ashikaga et al. 2013) or fibrosis (McDowell et al. 2015), and in some cases, the torso geometry (Jolley et al. 2008, 2010), is reconstructed from clinical imaging modalities. Clinical electrophysiological information has also begun to be incorporated in simulation studies (Krummen et al. 2012; Sohal et al. 2014). This new level of heart rhythm modelling has placed heart models on the pathway to becoming capable of representing the electrical responses of the heart to inputs from existing devices, such as pacemakers and defibrillators (particularly implantable cardioverter defibrillators (ICDs)), as well as suggesting new strategies for arrhythmia risk stratification and anti‐arrhythmia therapies. In this article, we review the current state‐of‐the‐art in using computer modelling as applied to human anti‐arrhythmia therapies. Specifically, we focus on simulations that have used human heart models only, at the tissue and organ level, to model anti‐arrhythmia treatments such as pacing for termination of atrial fibrillation (AF) and ventricular defibrillation, pharmacological studies, as well as the use of biophysically detailed computer models of the heart for risk stratification of arrhythmias. We present the basic principles of how such models are developed, along with how simulations of human arrhythmias, as well as patient heart–device interactions, can be used to improve the treatment of patients with arrhythmias. The content of this review is far from being exhaustive regarding the developments in the field; rather, it presents a glimpse of how computer modelling of heart electrical (dys)function can be used to address clinically relevant problems.

Overview of modelling principles and methodology

Computer modelling of electrophysiology has made enormous progress over the last decade. This section reviews briefly the methodological basis and advancements in biophysically based models of heart function. A schematic diagram of the current state‐of‐the‐art general approach to 3‐D multiscale (from the molecule to the organ) electrophysiology modelling (atrial or ventricular) is shown in Fig. 1. Modelling the electrophysiology of the heart, even in its most simple mathematical representation, involves propagation of an electrical impulse (cell action potential) in a three‐dimensional network of cells. The vast majority of these models involve biophysically detailed cell membrane kinetics, i.e. ionic currents, pumps and exchangers, the mathematical description of which is based on the formalism introduced by Hodgkin & Huxley (1952). The ionic exchanges across cell membranes, represented by the action potential ionic model comprising numerous ordinary differential and algebraic equations, drive current flow in the tissue.

Figure 1. Multiscale approach to image‐based modelling of cardiac electrophysiology .

Passive electrical coupling of cardiac cells mediates the tissue‐scale propagation of bioelectric impulses that originate at the membrane level (action potentials). 3‐D geometrical models are reconstructed from images. (Modified with permission from Trayanova et al. 2014.)

In tissue, atrial and ventricular myocytes are electrically connected via low‐resistance gap junctions. Ionic current can flow from cell to cell via this pathway, in addition to the current exchange between intracellular and extracellular spaces through cell membrane proteins. Propagation of the action potential is typically modelled using spatially continuous models that are viewed as resulting from a local spatial homogenization of behaviour in tissue compartments (membrane, intra‐ and extracellular spaces). Current flow in the tissue structure is typically governed by the monodomain reaction–diffusion partial differential equation (PDE) over the tissue or organ volume, with the use of conductivity tensor fields. Simultaneous solution of the PDE(s) with the set of ionic model equations (Vigmond et al. 2002, 2003; Plank et al. 2008) represents simulation of electrical wave propagation in the heart. The conductivity tensor fields used in these continuous models integrate all the information about the distribution of gap junctions over the cell membranes as well as the fibre, sheet and other microstructure organization in the atria and ventricles. Cardiac tissue has orthotropic passive electrical conductivities that arise from the cellular organization of the myocardium into fibres and laminar sheets. Global conductivity values in the atrial or ventricular model are obtained by combining fibre and sheet organization with myocyte‐specific local conductivity values.

Multiscale models of human heart electrophysiology are typically modular, allowing the use of a variety of cellular ionic models (Courtemanche et al. 1998; Nygren et al. 1998; ten Tusscher & Panfilov, 2006; Fink et al. 2008; Maleckar et al. 2009; Grandi et al. 2010, 2011; O'Hara et al. 2011), with different levels of biophysical detail. Solutions are executed on user‐specified organ geometries, typically individual hearts’ (atria and/or ventricles) geometry and structure (Aslanidi et al. 2011; Relan et al. 2011; McDowell et al. 2012; Krueger et al. 2013; Prakosa et al. 2014; Ukwatta et al. 2015), most often obtained from clinical magnetic resonance imaging (MRI). Clinical MRI scans with a contrast agent (late gadolinium enhancement, LGE) can also be used to visualize the structural remodelling in atria and ventricles (Nazarian et al. 2005; Akoum et al. 2011; Ukwatta et al. 2015). Figure 2 A presents ventricular model generation from clinical LGE‐MRI images, as described in a recent paper (Ukwatta et al. 2015). Atrial geometries used in electrophysiological simulations are acquired using MRI data (Virag et al. 2002; Dang et al. 2005; Jacquemet et al. 2005; McDowell et al. 2012, 2013; Ukwatta et al. 2014) as well as CAT data (Ridler et al. 2011). Figure 2 B illustrates the construction of a geometric model of the patient atria from clinical LGE‐MRI scans, as described recently (McDowell et al. 2012, 2013, 2015); in this case the patient atria show a significant amount of fibrotic remodelling. Since the atria are much thinner than the ventricles, image‐based models of at least one of the human atrial chambers can further be sub‐classified into surface and volumetric models. Surface models represent atrial geometry in 3‐D but neglect wall thickness (Vigmond et al. 2001, 2004; Virag et al. 2002; Dang et al. 2005); the latter is not true for volumetric models (Freudenberg et al. 2000; Harrild & Henriquez, 2000; Seemann et al. 2006; Reumann et al. 2008; Aslanidi et al. 2011; McDowell et al. 2012, 2013, 2015).

Figure 2. Constructing image‐based models of the ventricles and the atria .

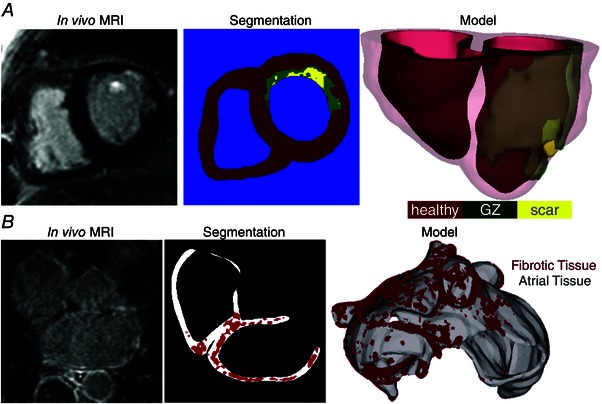
A, construction of a patient‐specific ventricular model of arrhythmia from a clinical MR scan. Images are shown of an infarcted patient heart before ablation (treatment) and the corresponding segmentation: healthy (red), GZ (green), or scar (yellow). An image of the 3‐D geometric model of the patient heart rendered with the epicardium and the infarct border zone semi‐transparent is shown in the third panel. (Modified with permission from Winslow et al. 2012.) B, a model of the fibrotic human atria (right) generated from a patient LGE‐MRI scan (left) following segmentation (middle) into normal and fibrotic tissue (fibrotic lesions in red). (Modified with permission from McDowell et al. 2012.)

Local fibre directions in ventricular or atrial models of various species have traditionally been mapped based on ex vivo histological sectioning information or on diffusion tensor imaging (DTI). In human organ‐level heart models, fibre orientation is mapped either using an atlas human heart (Vadakkumpadan et al. 2012) or by employing rule‐based approaches (Krueger et al. 2011; Bayer et al. 2012; Dossel et al. 2012). The accuracy of atlas‐based and rule‐based approaches for incorporating fibre orientation in heart models has been evaluated by two studies, respectively: Vadakkumpadan et al. (2012) and Bayer et al. (2012). Both studies compared the outcomes of electrophysiological models that involved atlas‐ or rule‐based approaches vs. fibre orientation obtained from diffusion tensor MRI. For instance, results by Bayer et al. (2012) demonstrated that activation patterns from simulations with the rule‐based fibre orientation approach developed in that study and DTI‐derived fibre orientations were nearly indistinguishable, with relative differences ≤6%, absolute mean differences in activation times ≤3.15 ms, and positive correlations >0.99. These results convincingly show that the rule‐based algorithm is a robust alternative to DTI for assigning fibre orientation to computational heart models.

Finally, numerical approaches for simulating the electrical behaviour of the heart have been described in detail in previous publications, some of which offer comprehensive reviews on the subject (Jacquemet et al. 2008; Plank et al. 2008; Trayanova, 2011, 2014).

Pacing: anti‐arrhythmia pacing for atrial fibrillation termination

The ability to construct multiscale models of the electrical functioning of the atria, representing integrative behaviour from the molecule to the entire organ, has paved the way for the use of these models in AF management. In this section, we provide an example of modelling work that has been conducted to optimize anti‐tachycardia pacing for AF, applicable to those patients that have implanted devices.

Pacemaker‐based therapy for AF has been recognized as a possible alternative to drug therapy; today many pacemakers and ICDs include pacing algorithms for AF prevention and termination (Redfearn & Yee, 2006). As compared with electrical cardioversion, pacing has the advantage of being painless, safe and energy‐efficient in implantable devices. Most existing pacing algorithms deliver preventive therapies aimed to suppress AF triggers and reduce dispersion in atrial refractoriness (Ellenbogen, 2007). Uldry et al. (2010) recognized that with the use of an atrial model, a better understanding of the degree of local capture by pacing could be achieved, which might have important implications for the development of pacing algorithms for AF termination. The authors used a 3‐D surface model of the human atria and rapidly paced it at a cycle length shorter than that of the detected arrhythmia, from a single site, in an attempt to terminate AF. The results demonstrated that the septum was the only pacing site that yielded AF termination in both atria. However, capture was sporadic, and overall, did not result in AF termination or permanent changes in AF pattern. A new pacing scheme, shown in Fig. 3, was subsequently devised (Uldry et al. 2012), where the initial rapid septal pacing phase, this time from a large septal area (see Fig. 3, shown in red in the septal area, left), was followed by a slow septal pacing phase from the same location (at a cycle length longer than that of the detected arrhythmia) aimed at lengthening the action potential duration (APD) and thus eliminating any residual fibrillating wavelets that might have survived in areas distant from the septum during the rapid pacing phase. The new algorithm could suppress AF reentries in a more robust way than single site rapid pacing, with AF termination rate increasing from 10.2% to 20.2%. This simulation research provided an example of how realistic models of the atria can be used to generate new ideas and potential approaches to AF management optimization.

Figure 3. Simulations of AF management with pacing .

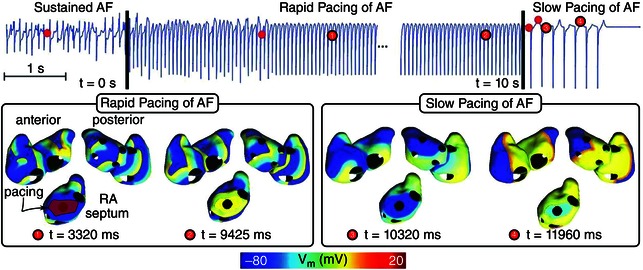
A dual stage septal pacing algorithm is presented with successful AF termination in a 3‐D surface model of the human atria. (Modified with permission from Uldry et al. 2012.)

This research was further extended in a recent paper by Rusu et al. (2014). Since AF can have different clinical forms corresponding to different patient‐specific atrial substrates, inter‐patient variability may affect the efficacy of septum pacing. Rusu et al. (2014) used computer simulations with the same atrial model as in the above study to assess the influence of electrophysiological heterogeneities (as occurring in the early stages of AF progression) on the ability to capture AF with rapid pacing from the septum area. Three different biophysical models of AF were considered: (i) AF in a homogeneous substrate (multiple wavelets), (ii) cholinergic AF arising from heterogeneities in vagal activation, and (iii) AF arising from heterogeneities in repolarization. The researchers found that in a homogeneous atrial substrate, AF capture could reach 80% of the atria. Heterogeneities, however, decreased the ability to capture during AF, in a manner that was different depending on the type of heterogeneities (those in vagal activation vs. those in repolarization). These model‐based results suggest that heterogeneities in atrial substrate greatly influence the ability to capture AF with rapid pacing from the septum area, and that AF pacing therapies in patients with implanted devices might need to be specific to each patient's atrial substrate.

More sophisticated 3‐D human atrial models have been recently developed (Colman et al. 2013; Tobón et al. 2013; Krueger et al. 2014) that incorporate biophysical detail on electrophysiological remodelling associated with persistent AF (for a review on recent efforts in AF modelling, the reader is referred to Trayanova 2014). The expectation is that such modelling efforts will also be directed, in synergy with providing mechanistic insight, towards addressing current clinical needs.

Pharmacological therapy: drug effects beyong the single cell

Relating effects of drugs on ion channels beyond the action potentials requires virtual tissue or whole heart organ simulation, so that arrhythmia onset, termination and prevention can be explored. Moreno et al. (2011) incorporated both state‐dependent Markov modelling of drug effects and full integration to the human action potential, human tissue, and finally realistic MRI image‐based human heart. This is the first instance of such massive integration across the space and time scales at play. Their study showed that the effects of flecainide and lidocaine (lignocaine) on sodium current (I _Na) block are globally similar in response to dynamic protocols. However, clinical trials have shown previously that flecainide tended to be proarrhythmic at therapeutic doses, whereas lidocaine was not. Simulation results made clear that neither simple reduction in I _Na nor single‐cell behaviour could explain this paradox. However, at the macroscopic scale, the vulnerable window was greater for flecainide than for lidocaine (especially in heart failure simulations due to shortened diastole) and reentrant arrhythmia in the ventricle persisted; as discovered by examining Markov states, this was due to the relatively slow accumulation of, and recovery from, use‐dependent block with flecainide.

A common approach to testing potential drugs for cardiotoxicity is to measure hERG channel‐binding affinity, which indicates whether a compound will prolong the QT interval of the ECG (ECG interval between ventricular depolarization and repolarization) by blocking the rapid delayed rectifier potassium current (I _Kr). Many recent studies have sought to use computer modelling to overcome the limitations of this screening methodology, such as its high rate of false positives and false negatives. Wilhelms et al. (2012) use detailed multiscale models of healthy and ischaemic hearts to examine the effects of two drugs that both fail the hERG screening test: cisapride, which is pro‐arrhythmic, and amiodarone, which is anti‐arrhythmic. Simulations revealed that the amiodarone is comparatively safe because in addition to QT prolongation (which was seen for both drugs on simulated ECGs) it also flattened APD restitution. This study and others (Dux‐Santoy et al. 2011; Carusi et al. 2012; Trenor et al. 2013; Zemzemi et al. 2013; Di Veroli et al. 2014; Loewe et al. 2014; Mishra et al. 2014; Romero et al. 2014; Yuan et al. 2015; Zemzemi & Rodriguez, 2015) demonstrate the feasibility of predicting specific drug dose effects on the thoracic ECG. It is hoped that this approach will lead to the development of screening systems that will accelerate cardiotoxicity testing by providing improved reliability compared to the present standard.

Defibrillation: heart–torso models and novel methodologies

Defibrillation by strong electric shock is the only known procedure that reliably terminates ventricular fibrillation (VF). A number of simulation studies have been conducted to determine computationally the defibrillation thresholds (DFTs) associated with different ICD configurations. Torso models have been developed for this purpose over the years; typically, they have involved reconstruction of a human torso and the heart (typically a normal heart) from CAT scans. An example of a finite‐element model used to determine DFTs, reconstructed from a CAT scan of a normal human torso, is shown in Fig. 4 A–C; it was used for the modelling of subcutaneous ICD electrodes (Jolley et al. 2010). While such model studies (Eason et al. 1998; de Jongh et al. 1999; Hunt & de Jongh Curry, 2004, 2006; Jolley et al. 2008, 2010; Russomanno et al. 2008) have provided an understanding of the current flow in the human resulting from the various placements of the defibrillation leads, they did not simulate the process of defibrillation, where the cell membrane responses to electric shocks have to be incorporated, but rather used the criterion of static extracellular potential gradient values above 5 V cm⁻¹ in more than 95% of the volume of the passive ventricles during the shock as a surrogate for the DFT (Fig. 4 D). This criterion is based on the critical mass hypothesis, which postulates that a defibrillation shock is successful if it produces a strong extracellular potential gradient over a large amount of ventricular tissue mass (Zipes et al. 1975).

Figure 4. Passive heart–torso models: imaging and computational pipeline and optimization of ICD electrode positions to minimize DFT .

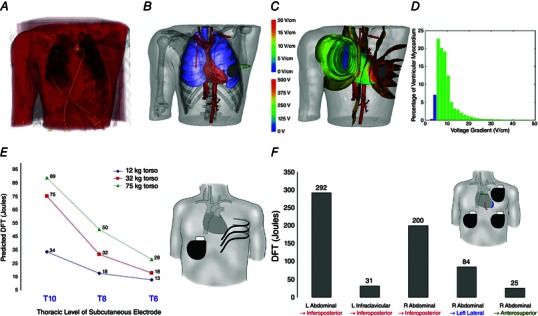
A, rendering of original CAT scan. B, electrode placement. C, visualization of isopotential surfaces (lower scale, volts) and voltage gradients on the cardiac surface (upper scale, V cm⁻¹). D, example of a graph of the percentage of ventricular myocardium versus voltage gradient for 500 V potential difference. (A–D, modified with permission from Jolley et al. 2010.) E, effect of varying positions of 25 cm subcutaneous electrode with right abdominal can on DFT. A trend for increased DFT with torso size is also evident. F, optimization of epicardial coil and can electrode placement in a 75 kg torso. Coils are shown as coloured lines overlying the heart silhouette in the following locations: red, inferoposterior; blue, apical; green, anterosuperior. (E and F, modified with permission from Jolley et al. 2008.)

While extracellular potential gradients are a determinant of post‐shock activity in the heart, other mechanisms are at play as well that involve diverse membrane responses to shocks (Knisley et al. 1999; Trayanova, 2001; Arevalo et al. 2007), as determined from experimental and simulation studies of isolated tissue and heart preparations. Indeed, not only transmembrane potential (V _m) gradients but also cardiac tissue structure is responsible for virtual electrode polarizations (VEPs; depolarizing and hyperpolarizing changes in V _m in response to an electric field) that can generate or abolish wavefronts (Efimov et al. 1998; Trayanova et al. 1998; Rodriguez & Trayanova, 2003; Efimov & Ripplinger, 2006). In addition, not only what happens during the shock but also events after the shock determine defibrillation outcome (Aguel et al. 1999; Anderson et al. 2000; Rodriguez et al. 2004), particularly in the case of graded responses (Trayanova et al. 2003; Bourn et al. 2006) or tunnel propagation (Ashihara et al. 2008; Constantino et al. 2010).

In addition to not incorporating the processes taking place during activation and repolarization of the heart, heart–torso defibrillation models historically involved other limitations resulting from the lack of appropriate imaging data. These included the use of a canine heart model within the human torso (Eason et al. 1998), not accounting for fibre architecture and tissue anisotropy (de Jongh et al. 1999; Tilg et al. 2002; Berger et al. 2006; Russomanno et al. 2008; Vanheusden et al. 2012), or only estimating the myocardial surfaces based on a certain distance from ventricular blood masses, but not detecting and modelling the myocardial volume itself (Tilg et al. 2002; Berger et al. 2006). Limitations associated with the lack of appropriate imaging data have been recently overcome, and human heart–torso models aimed at determining the DFTs associated with different ICD configurations (both transvenous and extracardiac) in a variety of patient groups, including paediatric and congenital heart disease (CHD) patients (Jolley et al. 2008, 2010) have been developed from torso imaging data. Generator (can) location, lead location, length, geometry and orientation, and spatial relation of electrodes to ventricular mass were systematically examined. Transvenous orientations typically resulted in the lowest DFTs, but subcutaneous arrays and epicardial placements were also clinically feasible. Figure 4 E presents the effect of varying positions of a subcutaneous electrode with right abdominal can on DFT. It can also be seen that DFT increased with torso size. Optimization of electrode/can placement was also performed in this torso by changing the anatomical relations of electrodes to the heart and by varying the length of the epicardial electrode. Figure 4 F shows the effects of anatomical variations in electrode configuration designed to position the heart more directly in the vector created from anode to cathode, resulting, as seen in the figure, in a 10‐fold difference in predicted DFT.

A recent study Rantner et al. (2013 b) made the first attempt towards developing a full‐blown biophysically detailed heart–torso model, one that represents the processes taking place during activation and repolarization of the heart. The new model was used to address a clinical need, namely that ICDs with transvenous leads often cannot be implanted in a standard manner in paediatric and CHD patients; currently, there is no reliable approach to predict the optimal ICD placement in these patients. The study provided the proof‐of‐concept that patient‐specific biophysically detailed computer simulations of the dynamic process of defibrillation could be used to predict the optimal location of the ICD leads in these patients. A pipeline for constructing personalized, electrophysiological (including both membrane kinetics and fibre orientation in the ventricles) heart–torso models from clinical MRI scans was developed and applied to a paediatric CHD patient, and the optimal ICD placement was determined using patient‐specific simulations of defibrillation. Figure 5 shows the various configurations tested, as the shock was delivered to an on‐going VF at different instants of time. In a patient with tricuspid valve atresia, two configurations with epicardial leads were found to have the lowest DFT. The study also demonstrated that determining extracellular potential gradients during the shock – without actually simulating defibrillation – was not sufficient to predict defibrillation success or failure. The study proved that using such methodology, the optimal ICD placement in paediatric/CHD patients could be predicted computationally, which could reduce defibrillation energy if the pipeline is used as part of ICD implantation planning.

Figure 5. Model and simulation results from the biophysically detailed heart–torso model of a paediatric CHD patient .

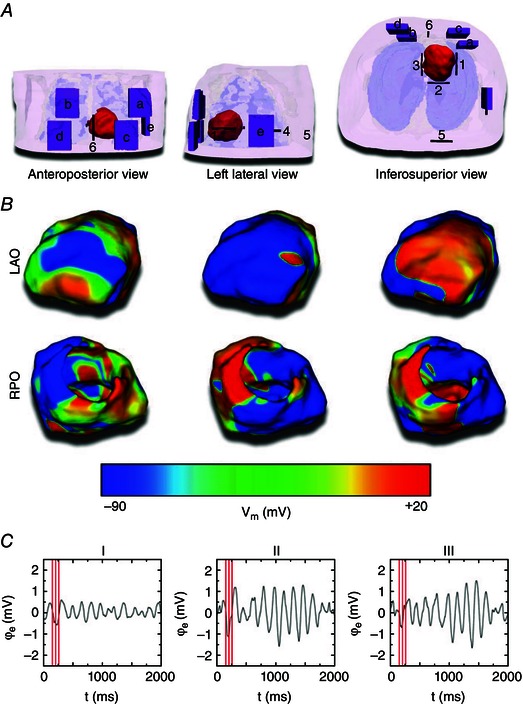
A, the finite element heart–torso mesh and ICD can (purple; a–e) and ICD lead (black; 1–6) placement locations. The ventricles are shown in red, skin in transparent pink, bones in transparent white, and lungs in transparent blue. Segmented and modelled, but not shown here, were fat, blood, muscles and remaining conductive medium. B, VF as shown in left anterior oblique (LAO; top row) and right posterior oblique (RPO; bottom row) V _m maps of three VF phases to which defibrillation shocks were applied. C, limb lead ECG traces of VF. Red lines mark the three VF phases from B. (Modified with permission from Rantner et al. 2013 b.)

Recently, defibrillation modelling has focused on the development of new methodologies for low‐voltage termination of lethal arrhythmias or for applying defibrillation in novel, less damaging ways. Although these studies were not performed using human hearts (Tandri et al. 2011; Rantner et al. 2013 a; Weinberg et al. 2013), we provide a brief example, due to potential clinical significance and impact, and because organ‐level heart simulations were involved. The study by Tandri et al. (2011) used sustained kilohertz‐range AC fields for arrhythmia termination, and was aided by whole heart ventricular modelling to reveal mechanisms. The article provided proof of the concept that electric fields, such as those used for neural block, when applied to cardiac tissue, similarly produce reversible block of cardiac impulse propagation and lead to successful defibrillation; it also showed that this methodology could potentially be a safer means for terminating life‐threatening reentrant arrhythmias. Since the same AC fields block equally well both neural and cardiac activity, the proposed defibrillation methodology could possibly be utilized to achieve high‐voltage yet painless defibrillation.

Ablation target prediction: using models of infarct‐related ventricular tachycardia and atrial fibrillation

The advances in MRI have facilitated acquisition of the intact structure of explanted hearts with high resolution. Leveraging these advances, a new generation of whole‐heart image‐based models of animal hearts with unprecedented detail, with or without structural remodelling, has emerged (Bishop et al. 2010; Vadakkumpadan et al. 2010). Such models have been used, in combination with experimental electrophysiological data, to provide better understanding of the role of the individual infarct region morphology in the generation and maintenance of infarct‐related ventricular tachycardia (VT), the most frequent clinical ventricular arrhythmia, present in 64% of patients with ventricular rhythm disorder and in 89% of patients with sudden cardiac death (SCD) (Stevenson et al. 1985). Such simulation methodology could have a major clinical impact in predicting the optimal targets for catheter ablation of infarct‐related VT in individual hearts, should the methodology be able to reconstruct patient hearts from clinical imaging data and evaluate the 3‐D patterns of infarct‐related VT in the patient. The first attempts in this direction have already been made. Studies by Relan et al. (2011) and Pernod et al. (2011) combined geometrical model construction from clinical MRI scans with invasive electrophysiological measurements to achieve personalized models of VT, with the goal of using them to guide clinical ablation. In these models, however, cardiac tissue was segmented out into scar and normal tissue, without the inclusion of a border zone (also termed grey zone, GZ, based on appearance on the MRI scan), which has been shown experimentally to be very arrhythmogenic (Schmidt et al. 2007).

Figure 6 A presents a schematic diagram of patient‐specific ventricular model development that incudes the segmentation of the infarct zone into scar and GZ, as illustrated in a recent publication (Ukwatta et al. 2015). In Fig. 6 B a simulation is shown of arrhythmia in a patient‐specific model of the infarcted ventricles from the study by Ashikaga et al. (2013). The study, based on 13 patient‐specific models, demonstrated that non‐invasive simulation prediction of infarct‐related VT is feasible; similar conclusions were later made by Ringenberg et al. (2014, 2015) based on two patient‐specific heart models. This approach could potentially be extended to the prediction of the optimal ablation sites in patients, without the invasive acquisition of personalized electrophysiological data.

Figure 6. Ablation target prediction .

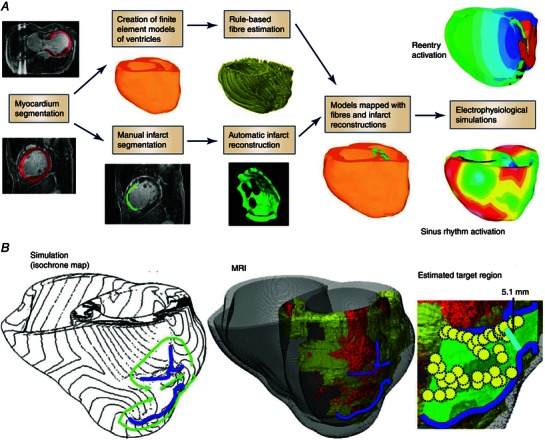
A, block diagram for generation of models of individual hearts from LGE‐MRI images for electrophysiological simulation studies. (Modified with permission from Ukwatta et al. 2015.) B, comparison between simulation‐guided and standard electrophysiological approaches for identifying ablation targets in two patients with infarct‐related VTs. Left panel: propagation pathways (green) and lines of conduction block (blue) are overlaid over VT activation maps simulated in image‐based patient heart models. Middle panel: pre‐ablation infarct geometry (infarct scar: orange; border zone: yellow; and non‐infarcted: grey) along with ablation lesions delivered by the standard approach (red circles) and conduction block lines as calculated from ventricular simulations. Right panel: optimal ablation zones (green shading) predicted by simulations, with narrowest isthmuses indicated (cyan); in both cases, only a fraction of the ablation sites from the standard approach were within the predicted optimal ablation zone (yellow circles). (Modified with permission from Ashikaga et al. 2013.)

To be able to advance the use of patient‐specific modelling studies towards non‐invasive prediction of optimal ablation sites in patients, certain obstacles have to be overcome. In particular, it is important to explore how well the whole heart model reconstructed from late‐enhancement MR imaging by thresholding the infarct into scar and border (grey) zone predicts the infarct‐related VT circuits, and specifically, how well their organizing centres (isthmuses, regions of block, etc.), which constitute targets of ablation, match experimental data. Since human experimental data are not available, we here briefly review a recent study by Deng et al. (2015) in pig hearts (similar in size to human), where the authors compared simulated and experimental epicardial activation maps obtained with a multi‐electrode sock. Importantly, the study examined the accuracy of the reentrant circuit location prediction when models of the same hearts are reconstructed from high resolution as well as low resolution clinical MRI scans. Results of the reconstructions showed that the geometry of the ventricles, including the infarct as well as isthmuses and channels in the scar, could be accurately obtained from low (clinical) resolution images (Fig. 7 A), and the arrhythmia utilizing these pathways in the scar could be calculated (Fig. 7 B and C shows an endocardial reentry with epicardial breakthrough). Importantly, all models, regardless of image resolution, accurately predicted the VT morphology and circuit location induced in the experiment (Fig. 7 D). These results are consistent with findings by Arevalo et al. (2013), which showed that incorporating heterogeneities (up to a level determined by experimental measurements) in the border zone did not change the locations of the organizing centres of infarct‐related VT, thus justifying the use of scar and GZ thresholding in reconstruction of patient‐specific ischaemic cardiomyopathy models from clinical MR scans. These results demonstrate that MRI‐based computer models of hearts with ischaemic cardiomyopathy could provide a unique opportunity to predict and analyse VT resulting from specific infarct architecture, and thus may assist in clinical decisions to identify and ablate the reentrant circuit(s). This potential needs, however, to be confirmed in human studies, both retrospective as well as prospective.

Figure 7. Pig heart simulation and experimental results regarding infarct‐related VT .

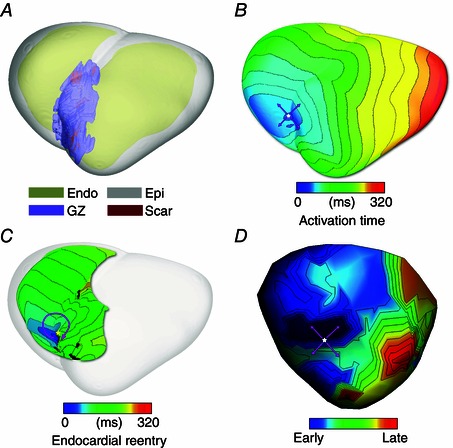
A, ventricular model construction from clinical resolution scans (including infarct scar and border zone), with the epicardium rendered semi‐transparent. B, simulated VT with epicardial breakthrough pattern shown (pink arrows: propagation direction). C, the same VT, but with endocardial view shown, demonstrating reentrant activity being sustained by propagation through isthmuses in the scar. D, experimentally recorded epicardial activation showing breakthrough pattern as well. (Modified with permission from Deng et al. 2015.)

Similar to human ventricular modelling, human atrial models have been used to optimize AF ablation, attempting to suggest strategies to minimize the size of ablation lesions. A set of studies (Dang et al. 2005; Ruchat et al. 2007) explored the effectiveness of ablation line patterns that are less invasive than the Maze III procedure and demonstrated that any such pattern needs to include ablation lines in both right atrium and left atrium so that a multiple‐wavelet AF can be successfully terminated. Recently, human tissue (Ashihara et al. 2012) and organ‐level atrial models aimed at studying AF ablation have begun to represent fibrotic structural remodelling associated with persistent AF. McDowell et al. (2012, 2013) created the first model of patient atria with fibrotic remodelling by segmenting out the enhanced regions in the LGE‐MRI scans; similar approaches followed (Krueger et al. 2014). Recently, McDowell et al. (2015) provided the first proof‐of‐concept that patient‐specific atrial models which combine atrial structure and fibrosis distribution from clinical MRI and representation of remodelled atrial electrophysiology could be used to predict how the fibrosis distribution determines the dynamic behaviour of persistent AF rotors and the optimal ablation targets in each patient. Patient‐specific distribution of fibrosis was found to be a critical component of AF initiation and maintenance. When the restricted regions encompassing the meander of the persistent phase singularities were modelled as ablation lesions, AF could no longer be induced (Fig. 8). The study demonstrates that a patient‐specific modelling approach to identify non‐invasively AF ablation targets prior to the clinical procedure is feasible. The electrophysiological representation of fibrotic remodelling in the human atrial models remains controversial, however, because of the lack of experimental data. Similarly, the segmentation of the LGE‐MRI fibrotic regions, and even the segmentation of the geometry of the thin atria from clinical MRI, is fraught with uncertainty and is an area of intense image‐processing research. Finally, AF is a complex disease, involving triggers from pulmonary veins, remodelling of cardiac nerves, etc., and models will need to explore which aspects of the disease will need to be represented under which circumstances to achieve maximum clinical fidelity of a particular targeted simulation approach.

Figure 8. V_m maps at five time instants in a human fibrotic left atrium (shown in Fig. 2 B) following pacing from two different pacing locations .

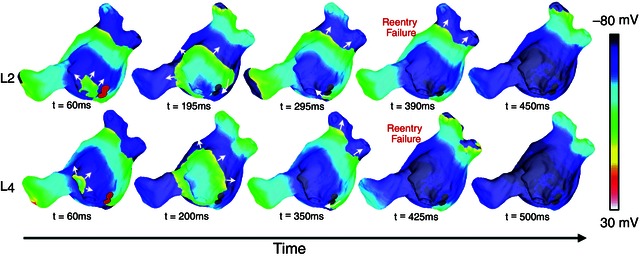
Pacing from these locations resulted in AF; however, incorporating targeted ablation lesions at the regions of organization of the reentrant circuits (the regions of phase singularity meander) resulted in AF being non‐inducible. Filled red circles (left‐most column) represent the extent of the ablation lesions. White arrows indicate direction of propagation. (Modified with permission from McDowell et al. 2015.)

Arrhythmia risk prediction: modelling to determine markers of arrhythmia risk

Robust methods for stratifying the risk of lethal cardiac arrhythmias decrease morbidity and mortality in patients with cardiovascular disease and reduce healthcare costs (Goldberger et al. 2011). The most widely used approaches currently used for stratifying risk of cardiac arrhythmias involve testing for abnormalities in the ECG, then using the results to identify patients who would benefit from ICD therapy. ECG‐based risk stratification methods scan for abnormalities in ventricular depolarization (late potentials (Kuchar et al. 1987) and a fractionated QRS complex (ECG waves during ventricular depolarization) (Das et al. 2006) and repolarization (T‐wave alternans; Rosenbaum et al. 1994), QT variability or dispersion (Berger et al. 1997; Couderc et al. 2007)). However, the mechanisms underlying these ECG indices, and their relationship to lethal cardiac arrhythmias, are not fully understood. This lack of knowledge probably explains why results of clinical trials to correlate surface ECG indices to lethal cardiac arrhythmias are often contradictory (Goldberger et al. 2011). Computational models of the heart are making initial inroads in this clinical cardiology arena (see Krummen et al. 2012, for example).

Research has reported a strong correlation between increased arrhythmia risk and the presence of T‐wave alternans (Narayan, 2006; Qu et al. 2010). In the clinical setting, testing for microvolt T‐wave alternans (MTWA) has particularly shown promise for dichotomizing patients who would and would not benefit from ICD therapy (Bloomfield et al. 2006; Hohnloser et al. 2009). However, the mechanistic basis of MTWA preceding lethal ventricular arrhythmias has been under debate. Until recently, it was believed that a steep APD restitution (>1) at rapid heart rates (Weiss et al. 2006) produces alternans in APD that underlies T‐wave alternans and the genesis of fibrillation (Pastore et al. 1999). However, MTWA is most successful in stratifying risk in patients at heart rates <110 beats min⁻¹, where APD restitution is flat (Narayan et al. 2007). Computational models of the left ventricle (LV) wall in combination with clinical data revealed that abnormal handing of intracellular calcium underlies alternans in action potential voltage, which results in MTWA at heart rates <110 beats min⁻¹ (Narayan et al. 2008; Bayer et al. 2010); abnormalities in intracellular calcium have long been linked to VF (Weiss et al. 2011; Merchant & Armoundas, 2012). Computational modelling studies have also shown that under the conditions of abnormal calcium dynamics, the magnitude of the T‐wave alternans is enhanced by structural heterogeneities in the myocardium (Doshi & Idriss, 2010).

Clinical studies have also revealed a correlation between AF severity (control vs. paroxysmal vs. persistent) and voltage alternans occurring in the atria, suggesting a novel marker for risk stratification in AF patients (Narayan et al. 2011; Lalani et al. 2013). As with MTWA, atrial voltage alternans occurred in AF patients at slow heart rates when APD restitution was <1, indicating that abnormal calcium dynamics may underlie atrial alternans associated with AF as well (Narayan et al. 2011). A recent computational modelling study explored the potential underlying mechanisms and showed that remodelling of the calcium handling system in human atrial cells could account for the onset and magnitude of APD alternans at slow heart rates (Chang et al. 2014); the predictive capabilities of the model were validated by matching the heart rate at alternans onset as well as alternans magnitude with those observed in the clinic. Furthermore, the authors precisely quantified the contributions of different AF‐remodelled calcium‐handling proteins to alternans onset at clinically relevant slow heart rates, allowing them to identify the key drivers of alternans in the model (Fig. 9). These potential mechanisms are in line with current understanding of calcium remodelling in AF patients (Voigt et al. 2012), thus providing compelling modelling predictions concerning the mechanisms of AF‐associated alternans, which may be tested experimentally in the future. Such approaches demonstrate the power of using computational models to provide insight into the mechanistic basis for clinical risk stratification markers.

Figure 9. Mechanisms of calcium‐driven instability underlying atrial voltage alternans associated with AF .

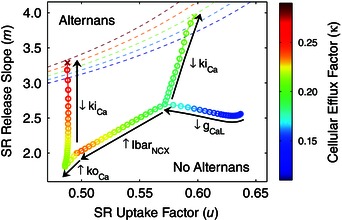
The effects of AF remodelling on calcium cycling stability were quantified in a human atrial action potential model using an iterated map analysis, formulated in terms of sarcoplasmic reticulum (SR) calcium release slope (m), SR calcium uptake factor (u), and cellular calcium efflux factor (κ). The threshold for stability is shown by the dashed lines for different values of κ, indicated by the colour bar, separating the alternans (unstable) region from the no alternans (stable) region. Sodium–calcium exchanger upregulation (Ibar_NCX) and increased ryanodine receptor activation (ko_Ca) slightly increased system stability (moving away from threshold); while L‐type calcium channel downregulation (g_CaL) and decreased ryanodine receptor inactivation (ki_Ca) decreased system stability (moving towards threshold), thus promoting alternans. (Modified with permission from Chang et al. 2014.)

An MRI‐based computational model of the human ventricles to demonstrate that detecting instabilities in the QT interval within the clinical ECGs can predict the onset of VT (Chen et al. 2011), particularly in patients with acute myocardial infarction (Chen et al. 2013). By having the ability to easily control the frequency and degree of premature activations in the model, the studies found that increased frequency of premature activation can precede the onset of VT, with the premature activations placing the system in a state where the QT interval is unstable. Therefore, screening the QT interval of the ECG for instabilities using the novel algorithm developed by Chen and Trayanova (Chen et al. 2011; Chen & Trayanova, 2012) could potentially be a robust risk stratification method for patients with acute myocardial infarction. These studies pave the way for executing computer simulations to determine patient‐specific thresholds for arrhythmia stratification ECG indices, rather than relying on clinical guidelines based on large and diverse cohorts of patients. Another approach for stratifying the risk of lethal cardiac arrhythmias that has recently gained traction is the use of computer models to predict the arrhythmia outcome in patients that exhibit potentially lethal mutations in genes encoding cardiac proteins associated with the long‐QT syndrome (Zhao et al. 2009; Benson et al. 2011; Jons et al. 2011; O'Hara & Rudy, 2012). These studies chart new directions for future genotype‐based risk stratification and personalized gene therapy.

Finally, a recent study (Vadakkumpadan et al. 2014) conducted a shape analysis to uncover whether the indices of left ventricular (LV) shape differ between patients with a high and low risk of SCD. By using clinical cardiac MRI and computational anatomy tools, a novel computational framework to compare 3‐D LV endocardial surface curvedness, wall thickness and relative wall thickness between patient groups was implemented. The framework was applied to cardiac magnetic resonance data of 61 patients with ischaemic cardiomyopathy who were selected for prophylactic ICD treatment on the basis of reduced LV ejection fraction. The study found that in patients with ischaemic cardiomyopathy and low LV ejection fraction, there exists quantifiable differences in 3‐D endocardial surface curvedness, LV wall thickness and LV relative wall thickness between those with no clinical events and those with arrhythmic or heart failure outcomes, reflecting adverse LV remodelling. This computational study demonstrated that regional LV remodelling indices have the potential to improve the personalized risk assessment for SCD.

The outlook for using modelling and simulation to address clinically relevant problems in heart rhythm disorder treatment

Over the last decades, cardiac models have been used extensively to gain insights into the mechanisms of arrhythmia in many disease settings and to understand how external currents can terminate ventricular arrhythmias. Currently, this trend continues to be strong, with cell, tissue and organ level studies contributing to major advances in our understanding of human heart rhythm and pump dysfunction. In addition, a major thrust in computational cardiac electrophysiology in the human has been to use models, particularly cellular and tissue level, as a test bed for evaluation of anti‐arrhythmic drugs, as reviewed briefly here. Advances have been made in testing hypotheses regarding the mechanisms of drug action on the scale of the whole heart; the latter work has the potential to more effectively guide the drug development pipeline – a process that currently has high failure rates and high costs.

As the trend to develop human cardiac computational models will continue in the future, atrial and ventricular electrophysiological modelling as a tool will necessitate continuous adaptation and integration of new elements, including model redesign and evaluation, improvements in the execution time of biophysically detailed atrial and ventricular membrane models, implementation of consistent strategies for comparison with experimental and clinical measurements, and investing in efforts to ensure repeatability and consistency of modelling results. The advancement in human whole‐heart electrophysiological modelling will continue to be strongly dependent on experimental and clinical measurements, which provide data to constrain, enrich and validate the models. Of particular importance to human whole‐heart modelling will be the capability to better resolve the structural features of the intact human heart by developing methods to characterize complex tissue geometries, such as that of the Purkinje system, and specifically, structural remodelling in disease. The development of unique and sensitive probes for the architecture of cardiac tissues, including tractography and connectivity mapping techniques, will provide a significant impetus to the human whole‐heart modelling efforts.

The use of heart models in personalized diagnosis, treatment planning, and prevention of SCD is also slowly becoming a reality. As demonstrated in this review, simulation studies have ventured into exploring cardiac electrophysiology in patients with implanted devices; progress has been made in optimizing the use of pacing for AF termination, in determining the most appropriate ICD configuration for deployment in subcutaneous defibrillation, and in CHD and paediatric patients, where no standard of therapy exists. Computer simulations of the function of the individualized diseased heart and its response to electrophysiological therapies such as pacing and defibrillation represent a profound example of a research avenue in the new discipline of computational medicine, and offer high promise for clinical translation. The feasibility of subject‐specific modelling is beginning to be demonstrated through the use of heart models reconstructed from clinical MRI or CAT scans. Biophysically detailed models of the atria and ventricles assembled with data from these clinical imaging modalities that incorporate electrophysiological and structural remodelling in cardiac disease are poised to become a first line of screening for new atrial and ventricular anti‐arrhythmia therapies and approaches, new diagnostic developments, and new methods for arrhythmia prevention. Implementing patient‐specific cardiac simulations at the patient bedside for arrhythmia therapy and management could become a thrilling example of computational approaches in translational medicine.

Currently, however, researchers face numerous obstacles in the development of patient‐specific heart models, including the low resolution of the in vivo heart scans, issues with segmenting out structural remodelling in the patient heart such as the infarct, and, finally, difficulties in validating these models with ECGs and patient electrophysiological data. Future studies will need to create the right balance between minimal invasiveness of the approach and the need to incorporate the correct amount of patient‐specific electrophysiological information, including autonomic influences. Furthermore, the advancement of algorithms and approaches for high‐speed simulations is of critical importance in order for these approaches to become clinical reality. Finally, the development and use of electrophysiological models of the heart currently requires a great amount of expertise in a number of different fields such as numerical analysis, computer science, cardiac electrophysiology, medicine and image processing. Efforts must be supported to develop a user‐friendly web‐based computing infrastructure that can facilitate the transition of personalized computational models into potential clinical tools. This infrastructure should allow the direct input of cardiac structural imaging data and the ability to easily assemble models with the click of the mouse.

Despite the numerous obstacles facing the development of patient‐specific heart models of rhythm dysfunction, we are poised at an exciting moment in cardiovascular medicine. The findings of the molecular biology of the heart, the emergence of new technologies for measuring the properties of cells, tissues and organ function, and the impact of Moore's law on computational modelling could finally come together to drive the creation of new, quantitative, model‐based approaches to understanding the function of the heart in disease, and the use of computational modelling of the heart at the patient bedside.

Additional information

Competing interests

None declared.

Funding

This work was supported by the 2013 National Institute of Health Director's Pioneer Award Program (1DP1HL123271‐01).

Biographies

Natalia Trayanova is the Murray B. Sachs Professor of Biomedical Engineering at Johns Hopkins University. She directs the Computational Cardiology Laboratory at the Institute for Computational Medicine. She is a recipient of the NIH Director's Pioneer Award for innovative science. Dr Trayanova is a Fellow of the Heart Rhythm Society, American Heart Association, Biomedical Engineering Society and American Institute for Medical and Biological Engineering. Research in her laboratory focuses on understanding cardiac electrical dysfunction, and on improving anti‐arrhythmia therapies using a personalized approach. Dr Trayanova is the author of over 200 peer‐reviewed publications in prestigious journals. She and her lab members have received numerous research awards. Dr Trayanova serves as Section Editor of the journals Heart Rhythm and Frontiers in Computational Physiology and Medicine, and is on the Editorial Board of several journals, including Heart Rhythm and American Journal of Physiology.

Kelly Chang is a doctoral student in Dr Trayanova's lab.