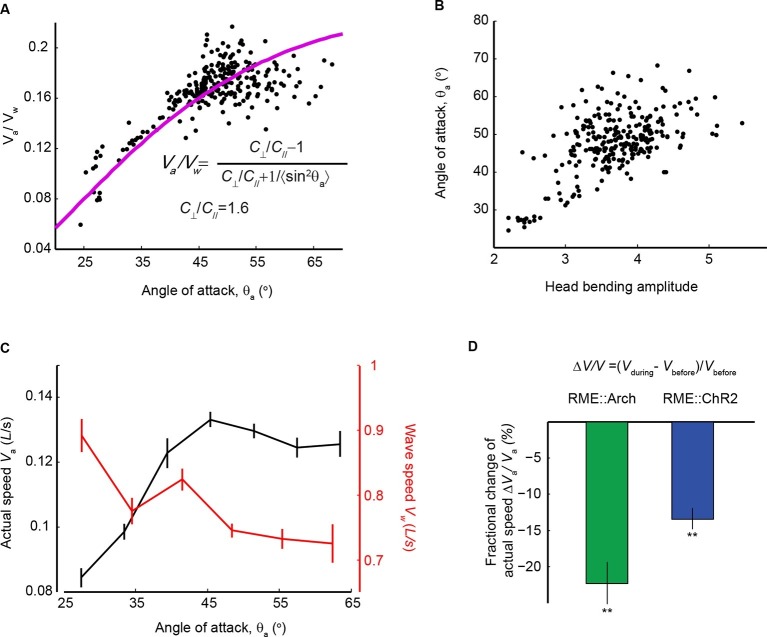
Figure 7. Head bending amplitude correlates with speed and efficiency of forward locomotion.
(A) The angle of attack, measured as the average angle of a body segment with respect to the direction of forward movement, is plotted with the propulsion efficiency, defined as the ratio of the actual speed Va to the propagation speed of undulation in the reference frame of a worm Vw. Magenta line is the theoretical fit according to the equation in the figure panel. In this equation, C⊥ is the drag coefficient perpendicular to the worm body and C// is the drag coefficient longitudinal to the worm body. C⊥/C// = 1.6, which is the best fitting parameter, agrees well with theoretical calculation in the small angle limit (Gray and Hancock, 1955). (B) The angle of attack increases with head bending amplitude (R = 0.57, p<10-23, Pearson’s correlation). In A and B, each dot represents one measurement from a bout (~10–15 s) of forward locomotion of wild-type animals in 25% dextran (w/v). (C) By binning the velocity data in (A) and (B), we replot the actual speed (Va, black) and propagation wave speed of forward locomotion (Vw, red) with the angle of attack. Propagation wave speed decreases with the angle of attack (R = −0.32, p<10–6, Pearson’s correlation). At around 45 degree angle, the actual speed of locomotion is maximized. For A-C, n > 100 bouts of forward movements from 10 worms, Mean ± SEM. (D) Optogenetic inhibition of RME neurons that express Arch (n = 11 trials, 5 animals) or optogenetic activation of RME neurons that express channelrhodopsin ChR2 (n = 34 trials, 5 animals) significantly reduces the actual speed of forward locomotion. For each trial, we calculate the change of actual speed of locomotion during and before optogenetic manipulation of RME, **p<0.01, Wilcoxon signed rank test for zero median, Mean ± SEM. Figure 7—figure supplement 1 shows the effects of optogenetic manipulation of RME activity on propulsion efficiency.
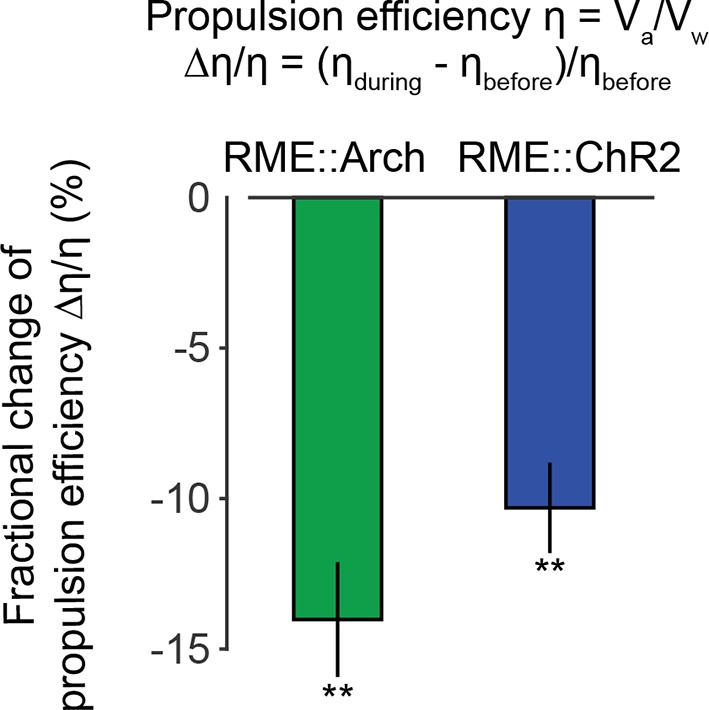
Figure 7—figure supplement 1. Optogenetically inhibiting RME neurons that express Arch (n = 11 trials, 5 animals) or optogenetically activating RME neurons that express channelrhodopsin ChR2 (n = 34 trials, 5 animals) significantly reduces propulsion efficiency of forward locomotion.