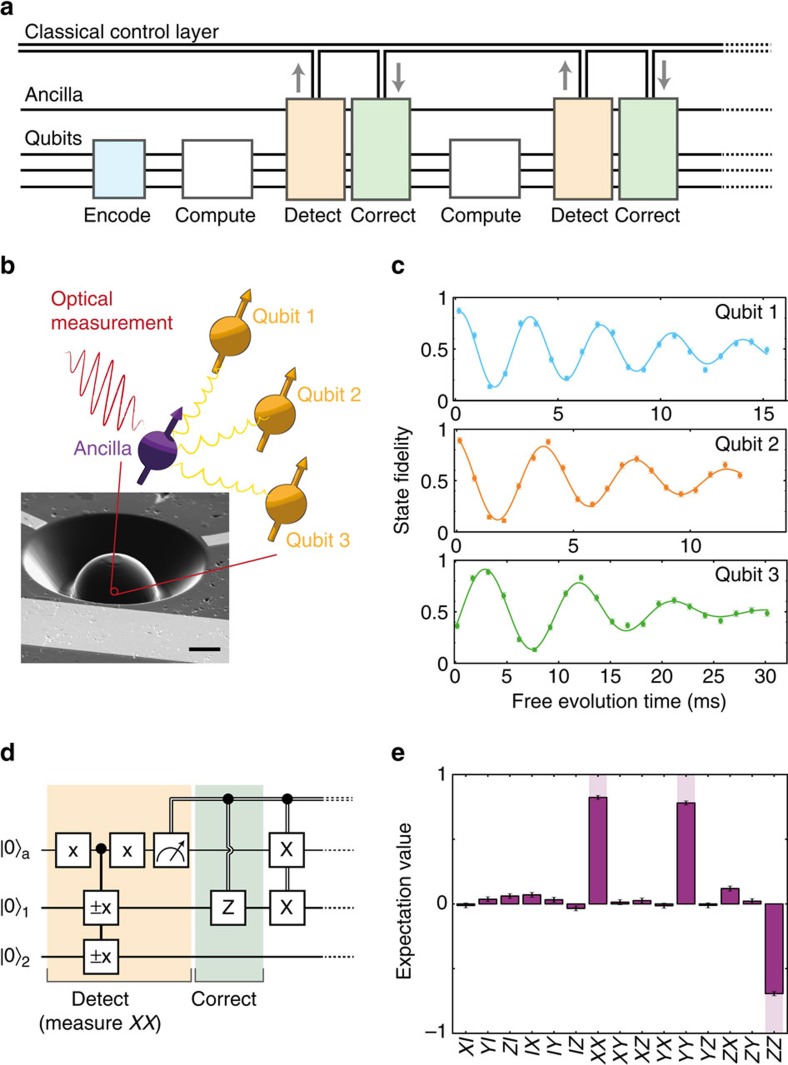
Figure 1. Quantum error correction and implementation of stabilizer measurements.

(a) A quantum state is encoded in a logical qubit consisting of three physical qubits. Errors inevitably occur, for example, during computations. An ancilla is used to repeatedly perform measurements that detect errors. Errors are corrected through classical logic and feedback, while the quantum state remains coherent and encoded. (b) Device: chemical-vapour-deposition-grown single-crystal diamond with a solid-immersion lens³⁷ and on-chip lines for microwave control. Scale bar, 5 μm. Ancilla: the optically addressable electronic spin of a nitrogen vacancy (NV) centre. Qubits: three ¹³C nuclear spins that are controlled and measured through the hyperfine coupling to the ancilla (Methods). (c) Free induction decay (Ramsey) experiments. Gaussian fits yield dephasing times 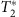=12.0(9), 9.1(6) and 18.2(9) ms for qubits 1, 2 and 3, respectively. (d) Deterministic entanglement of two qubits by XX stabilizer measurement and feedback. The ±x gates are π/2 rotations around x with the sign controlled by the ancilla state. The final X operations reset the ancilla and account for an additional X flip for the +1 outcome (Methods). (e) State tomography of the generated entangled state for qubits 2 and 3. The fidelity with the ideal state is F=0.824(7) (see Supplementary Fig. 6 for other qubit combinations and post-selected results). All error bars are one statistical s.d.