Genes influence the amplitude and timing of brain hemodynamic responses

Abstract

In functional magnetic resonance imaging (fMRI), the hemodynamic response function (HRF) reflects regulation of regional cerebral blood flow in response to neuronal activation. The HRF varies significantly between individuals. This study investigated the genetic contribution to individual variation in HRF using fMRI data from 125 monozygotic (MZ) and 149 dizygotic (DZ) twin pairs. The resemblance in amplitude, latency, and duration of the HRF in six regions in the frontal and parietal lobes was compared between MZ and DZ twin pairs. Heritability was estimated using an ACE (Additive genetic, Common environmental, and unique Environmental factors) model. The genetic influence on the temporal profile and amplitude of HRF was moderate to strong (24%–51%). The HRF may be used in the genetic analysis of diseases with a cerebrovascular etiology.

Introduction

The brain has limited energy reserves. As a consequence, its normal function is critically dependent on neurovascular coupling — the matching of blood flow with neuronal activity spatially and temporally (Iadecola, 2004). The signal change detected in functional magnetic resonance imaging (fMRI) reflects changes in blood oxygenation induced by neuronal activation. The temporal evolution of this signal change, termed the hemodynamic response function (HRF) reflects regulation of regional cerebral blood flow in response to neuronal activation. The shape of the HRF can be characterized by its height (H) or maximum signal change, time to maximum signal change (T), and full width at half maximum signal change (W). These HRF characteristics are influenced by vasodilatory signaling, blood vessel stiffness, neurovascular coupling delay, venous transit time, and the time constant of autoregulatory feedback (Buxton et al., 2004; Stephan et al., 2007).

The HRF varies between individuals (Aguirre et al., 1998) with moderate reliability over time within an individual (Shan et al., 2014). Knowing how much of the individual variation is due to inherited or acquired factors may yield a better understanding of cerebrovascular function in health and disease. To assess the contribution of genetic factors to HRF variability, here we estimate the heritability of HRF characteristics for the first time.

We tested whether HRF characteristics are heritable using fMRI data acquired during an N-back working memory task in 125 monozygotic (MZ) and 149 dizygotic (DZ) twin pairs. The 0- and 2-back working memory task (Blokland et al., 2011) activate the left (L) and right (R) middle frontal gyrus (MFG); L and R supramarginal gyrus (SMG); and L and R angular gyrus (AG). We estimated the HRF in each of these regions by fitting the convolution of the HRF, modeled as the sum of 2 gamma functions with 6 parameters, and a function representing neuronal activity, to the time course of the fMRI signal. We selected this HRF model because of its performance in terms of precision, accuracy and parameter identifiability (Shan et al., 2014).

Materials and methods

fMRI data

Data were acquired as part of a prior fMRI study (Blokland et al., 2011) forming part of the Queensland Twin Imaging Study (QTIMS) (de Zubicaray et al., 2008). The retrospective use of the data was approved by the Human Research Ethics Committee of the QIMR Berghofer Medical Research Institute and The University of Queensland in compliance with the Australia National Statement on Ethical Conduct in Human Research.

This study retrieved data from 125 monozygotic (MZ) and 149 dizygotic (DZ) twin pairs consisting of 340 females and 208 males with a mean age of 22.43 ± 2.47 SD (age range, 18–29 years). The detailed demographic data of the twin sample was reported in the previous study (Blokland et al., 2011). There are 92 and 57 DZ twin pairs with same and different genders respectively. The average full-scale intelligence quotient (FIQ) of the participants was slightly higher than that of the general population, but still followed a normal distribution (Blokland et al., 2011). There was no significant difference between co-twins of either zygosity in gestational age, birth weight, or parental socioeconomic status.

Participants performed the 0- and 2-back versions of the N-back working memory task. The detailed fMRI experimental procedure is described in detail in previous reports (Blokland et al., 2008; Callicott et al., 1998). In the N-back task, a series of numbers are presented on a screen. The 0-back condition required participants to respond to the number currently shown on the screen. The 2-back condition required participants to respond to the number presented 2 trials earlier. The number was presented for 200 ms with an 800 ms interval between stimuli, with 16 trials per block. In total, 16 alternating blocks were performed for the two conditions continuously (8 blocks per condition).

The 3D T1-weighted MR image and echo planar imaging (EPI) data analyzed in this study were acquired on a 4 T Bruker Medspec whole body scanner (Bruker, Germany). The 3D T1-weighted images were acquired using a MP-RAGE pulse sequence (TR = 2500 ms, TE = 3.83 ms, T1 = 1500 ms, flip angle = 15°, 0.89 × 0.89 × 0.89 mm³). For each participant, 127 EPI datasets (TR = 2.1 s, TE = 30 ms, flip angle = 90°, 3.6 × 3.6 × 3.0 mm³) were acquired continuously during the tasks.

Task performance during scanning was recorded and summarized by accuracy and response time. Task accuracy was defined as the ratio between the number of correct 2-back trials and the total number of 2-back trials. Task response time (RT) was defined as the averaged time between stimulus onset and subject response across all 2-back trials.

Genotyping

Details regarding the zygosity determination are as described previously (Wright and Martin, 2004). Zygosity was confirmed by genome-wide single nucleotide polymorphism genotyping (Illumina 610 K chip).

Image analysis

fMRI data were analyzed using Statistical Parametric Mapping (SPM8, the Wellcome Trust Centre for Neuroimaging, London, UK). The first five EPI volumes were discarded to ensure that tissue magnetization had reached steady state. The spatial preprocessing included two pass motion correction (Friston et al., 1995) and spatial normalization to the average brain T1 template (Ashburner and Friston, 1999). Normalized volumes were smoothed with an 8 × 8 × 8 mm³ full width, half maximum Gaussian kernel. We first determined locations of activation using the general linear model with a finite impulse response (FIR) basis function. The FIR was chosen as the basis function to minimize the assumptions made about the form of the hemodynamic response function (HRF). The 2-back minus 0-back t-contrast images were entered into a group-level random-effect (RFX) one-sample t-test to identify the common activation voxels (α < 0.05 with family wise error rate adjustment for multiple comparisons). The anatomical structures containing common activation voxels were selected as anatomic structures for HRF modeling: left (L-) and right (R-) middle frontal gyrus (MFG); L- and R-supramarginal gyrus (SMG); and L- and R-angular gyrus (AG) (Fig. 1c). These structures have been robustly associated with working memory in previous studies (Olesen et al., 2004). Regions of interest (ROIs) were defined as the overlap of an existing probabilistic atlas of each structure in stereotaxic coordinate space (Shattuck et al., 2008) with group activation regions. For each participant, the fMRI time course was extracted by averaging the signal intensity at each time point in the voxels with the top 12.5% of SPM t statistics within each ROI.

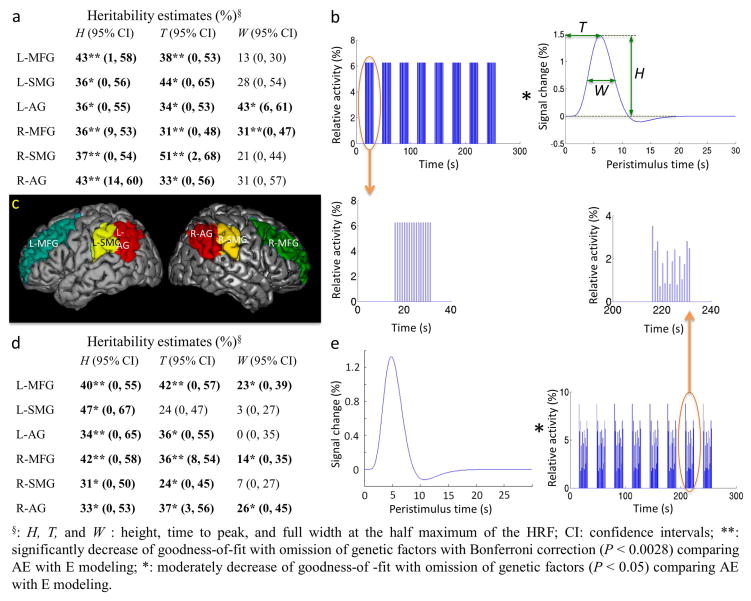
Fig. 1.

Estimating hemodynamic response functions (HRFs) and their heritability. Heritability was estimated using a full ACE (Additive genetic, Common environmental, and unique Environmental factors) model. The ACE model estimated the common environmental factors to be zero except for H (17%) and W (18%) in the left angular gyrus when the HRFs were estimated with a flexible neuronal activity function. (a) Heritability of HRF characteristics estimated with a fixed neuronal activity function. (b) HRF estimation by fitting convolution of the HRF with a fixed neuronal activity function, corresponding to the time course of stimulus presentation, to the time course of fMRI signal. (c) Anatomic structures within which HRFs were estimated. Left (L-) and right (R-) middle frontal gyrus (MFG), angular gyrus (AG), and supramarginal gyrus (SMG) were activated by the working memory task. (d) Heritability of HRF characteristics estimated with a flexible neuronal activity function (e) HRF estimation by fitting convolution of the HRF with a flexible neuronal activity function to the time course of fMRI signal.

Hemodynamic response function (HRF) modeling

The detailed methodology of HRF modeling has previously been reported in Shan et al. (2014). The HRF was estimated by fitting the fMRI time course with the convolution of HRF and neuronal activity functions. ROIs without fMRI activation (i.e., peak change in HRF < 0.2%) were excluded pairwise from heritability analysis. The number of MZ and DZ pairs with fMRI activation in each ROI is summarized in Table 1. The modeled HRFs were summarized by three characteristics: height (H), the maximum percent signal change; time-to-peak (T), the time for the signal to reach its maximum value; and width (W) as full width at the half maximum (Fig. 1b). These characteristics reflect the maximum (H), latency (T), and duration (W) of blood oxygenation changes caused by changes in local blood flow coupled to local neuronal activity.

Table 1.

Number of pairs with estimated HRFs for each region of interest (ROI).

ROI	Fixed neuronal activity function		Flexible neuronal activity function
	MZ pairs	DZ pairs	MZ pairs	DZ pairs
L-MFG	94	124	94	116
L-SMG	51	61	49	64
L-AG	68	93	71	83
R-MFG	95	133	89	131
R-SMG	64	85	67	90
R-AG	69	104	82	97

HRFs: hemodynamic response function characteristics, L-: left; R-: right; MFG: middle frontal gyrus; SMG: supramarginal gyrus; AG: angular gyrus; MZ: monozygotic twin; DZ: dizygotic twin.

Two neuronal activity functions were convolved with the HRF to fit the fMRI time course. (1) The fixed neuronal activity function assumes that the neuronal activity is the same as the time course of the stimuli presented in the experiments. It was constructed with a fixed start time specified by the experimental design and uniform amplitude for each trial within all blocks (Fig. 1b). (2) The flexible neuronal activity function allows variation in the delay in the neuronal response and in the response amplitude for each trial in a block of tasks:

$$u(t+\tau )=\{\begin{array}{cc}{\beta }_i/m,& t=\mathit{stimulus}on\mathit{time}\\ 0& t=\mathit{others}\end{array}$$

in which t is the actual time from the start of task, τ is the delay time, β_i are the amplitude parameters (i = 1, 2, … 16 in this study), and m is the number of trials in each block (m = 16 in this study) (Fig. 1e). The delay was initially set to 0 and all amplitude parameters were set to 1. Nonlinear least squares fitting was then used to estimate the delay time and amplitude parameters for neuronal activity changes that yielded the best fit for each individual. Further, the median amplitude, the inter-quartile range (IQR) of amplitude and the approximate entropy (ApEn) of neuronal activity changes were calculated. ApEn quantifies the unpredictability of fluctuations in a time series, i.e., ApEn is small for predictable time series with repetitive patterns (Pincus, 1991). ApEn was calculated as:

$$\begin{array}{l}\mathit{Apen}(S,m,r)=ln\left[\frac{C_m+(r)}{C_{m+1}(r)}\right],C_m(r)=\frac{{\displaystyle \sum _{i=1}^{N-m+1}}{C}_{im}(r)}{N-m+1},\text{and}\\ C_{im}(r)=\frac{n_{im}(r)}{N-m+1}\end{array}$$

where S represents the neuronal activity changes, m is the pattern length (m = 2 in this study), r is the similarity criterion (r = 2 × standard deviation of S in this study), N is the length of S, n_im(r) is the number of patterns that are similar to pattern i determined by the similarity criterion r, and C_im(r) is the fraction of patterns of length m that resemble the pattern of the same length to pattern i.

Simulation of HRF modeling with flexible neuronal activity function

Simulation studies were performed to test the ability to model neuronal responses using a flexible neuronal activity function. The fMRI data were simulated by the convolution of the HRF and the neuronal activity function (Shan et al., 2014). The Balloon Model was used to generate the HRF. To examine the ability to estimate variations in the amplitude of neuronal activity changes, this was decreased in 5% increments between 10% and 90% of activity. The number of trials in each block affected by the change in amplitude was varied systematically from the first trial in each block to the first 15 of a total of 16 trials in each block. The neuronal activity function was convolved with the simulated HRF and sampled to generate a simulated fMRI time course. Estimation of HRF characteristics was performed as described above. H and T of HRFs modeled from the simulated fMRI time course were compared with the true values, calculated from the HRF that was used to generate simulated data.

We also tested the ability to estimate HRF characteristics in the presence of random variations in neuronal activity and of noise. To ensure that a realistic temporal signal to noise ratio (SNR) was used in the simulation, we first estimated the temporal SNR in the fMRI datasets. Cubic volumes of interest (VOI), 3 × 3 × 3 voxels in size, were selected from the anterior cerebellum and the mid corpus callosum. Temporal SNRs were calculated as the ratio between the mean intensity in the fMRI time series (122 EPI volumes) and the standard deviation. The neuronal activity function was randomly varied and convolved with the HRF. Random noise was then added to the generated time course, with a temporal SNR of 150, selected on the basis of the histogram of estimated SNR from the whole group. The simulated fMRI time course was sampled with a TR of 2.1 s. The HRFs were then estimated using fixed and flexible neuronal activity functions. The simulation was executed 100 times. The number of simulation execution was determined by obtaining stable variability and performance (Shan et al., 2014). H and T of HRFs modeled from the simulated fMRI time course were compared with the true values, calculated from the HRF that was used to generate simulated data. The estimation error for the neuronal activity function was evaluated by the relative error in the time to onset of neuronal activity and by relative error in the amplitude of neuronal activity in all trials.

Correlations between estimated HRF characteristics, neuronal activation, and performance data

Pearson correlations between task performance and HRF characteristics or neuronal activity changes were calculated using SPSS20 (IBM, New York). Bivariate tests of significant difference in correlation coefficient from zero with two tails followed with false discovery rate (FDR) correction (FDR-q < 0.05) (Storey, 2002) was used to determine statistical significance.

Heritability analysis of HRF characteristics

To examine the heritability of the HRF, we first compared the resemblance of HRF characteristics in MZ and DZ twin pairs. For each HRF characteristic, the intra-class correlations (ICC) measuring absolute agreement in HRF characteristics within MZ and DZ twin pairs were determined with a two way random effects model using SPSS20 (IBM, New York). Tests of significant difference in ICC from zero was followed with Bonferroni correction (P < 0.0028) for multiple comparisons of 18 HRF characteristics to determine statistical significance.

The normality of all HRF characteristics was confirmed using Q–Q plots in SPSS20 (IBM, New York). The relative contribution of additive genetic factors to the variance of each HRF characteristic was estimated using a structural equation model implemented in the software package Mx (Neale and Miller, 1997). Phenotypic variances of MZ and DZ twins were constrained to be equal. Age and gender were included as covariates. MZ twin pairs were expected to share all of their genetic material whereas DZ twin pairs were expected to share, on average, half of their genetic material. Variances of HRF characteristics were decomposed into additive genetic factors (A), common environmental factors (C), and unique environmental factors, which also included measurement errors (E). For the full ACE model, common environmental factors were estimated to be zero. Thus, the significance of genetic factors was determined by comparing the goodness-of-fit of the AE model and the E model. Tests of significant difference in goodness-of-fit from zero were followed with Bonferroni correction (P < 0.0028) for multiple comparisons of 18 HRF characteristics. We also modeled non-additive genetic (D) influences using an ADE model by introducing an expected coefficient of 0.25 for non-additive effect.

Results

Heritability of HRF characteristics modeled with fixed neuronal activity function

MZ twins showed significant resemblance in all HRF characteristics in all regions of interest (ROIs) except W in right supramarginal gyrus, while DZ twins did not (Table 2). The high ICCs and the significant resemblance within MZ pairs and significant ICC difference between MZ and DZ pairs are strong evidence that HRF characteristics are heritable.

Table 2.

The intra-class correlations in HRF characteristics in twin pairs^a.

HRFs	Fixed neuronal activity functions		Flexible neuronal functions
	MZ pairs (95% CI)	DZ pairs (95% CI)	MZ pairs (95% CI)	DZ pairs (95% CI)
L-MFG-H	0.49** (0.23, 0.66)	0.23 (0, 0.46)	0.52** (0.26, 0.69)	0.33* (0.04, 0.54)
L-SMG-H	0.49** (0.12, 0.71)	0.14 (0, 0.49)	0.5** (0.11, 0.72)	0.19 (0, 0.51)
L-AG-H	0.56** (0.29, 0.73)	0.2 (0, 0.47)	0.66** (0.46, 0.79)	0.49* (0.19, 0.68)
R-MFG-H	0.56** (0.33, 0.71)	0.03 (0, 0.31)	0.51** (0.26, 0.68)	0.36* (0.11, 0.54)
R-SMG-H	0.59** (0.32, 0.75)	0.07 (0, 0.4)	0.5** (0.18, 0.69)	0.17 (0, 0.46)
R-AG-H	0.64** (0.41, 0.78)	0.09 (0, 0.38)	0.47** (0.18, 0.69)	0.07 (0, 0.4)
L-MFG-T	0.47** (0.2, 0.65)	0.26 (0, 0.48)	0.54** (0.29, 0.7)	0.37* (0.08, 0.56)
L-SMG-T	0.48* (0.1, 0.71)	0.31 (0, 0.58)	0.49** (0.11, 0.71)	0.03 (0, 0.42)
L-AG-T	0.55** (0.27, 0.72)	0.08 (0, 0.39)	0.51** (0.21, 0.69)	0.18 (0, 0.49)
R-MFG-T	0.51** (0.27, 0.68)	0.01 (0, 0.3)	0.55** (0.31, 0.7)	0.15 (0, 0.39)
R-SMG-T	0.54** (0.24, 0.72)	0.28 (0, 0.53)	0.49** (0.17, 0.68)	0.03 (0, 0.36)
R-AG-T	0.51** (0.2, 0.7)	0.05 (0, 0.36)	0.5** (0.22, 0.68)	0.13(0.34, 0.43)
L-MFG-W	0.4** (0.1, 0.6)	0.05 (0.35, 0.34)	0.49** (0.21, 0.67)	0.2 (0, 0.45)
L-SMG-W	0.51** (0.14, 0.72)	0.1 (0, 0.46)	0.09 (0, 0.49)	0.02 (0, 0.38)
L-AG-W	0.53** (0.24, 0.71)	0.20 (0, 0.47)	0.16 (0, 0.48)	0.4* (0.04, 0.63)
R-MFG-W	0.48** (0.22, 0.65)	0.15 (0, 0.39)	0.34* (0, 0.57)	0.2 (0, 0.43)
R-SMG-W	0.34 (0, 0.6)	0.17 (0, 0.46)	0.19 (0, 0.51)	0.03 (0, 0.43)
R-AG-W	0.39* (0.02, 0.62)	0.03 (0, 0.34)	0.52** (0.25, 0.69)	0.04 (0, 0.42)

Numbers in bold font refer to correlations with P < 0.05.

^aIntra-class correlations were calculated using a two way random model and the type of absolute agreement. There was no significant effect of age and sex on HRF characteristics. HRFs: hemodynamic response function characteristics, L-: left; R-: right; MFG: middle frontal gyrus; SMG: supramarginal gyrus; AG: angular gyrus; MZ: monozygotic twin; DZ: dizygotic twin; negative ICC values from SPSS are set to 0.

^**Significant correlations with Bonferroni corrections (P < 0.0028).

^*Moderate correlations (P < 0.05).

Of all models tested, the AE model had the lowest Akaike Information Criterion (AIC) value for all HRF parameters and regions except for W in the left middle frontal gyrus (Table 3). There were significant (P < 0.0028) genetic contributions to H and T for most ROIs (Fig. 1a). These results indicate a significant genetic influence on the amplitude and latency of the hemodynamic response induced by the activation of brain regions involved in working memory. The full ACE model estimated C to be zero. The ADE model goodness-of-fit was slightly better (lower AIC) than for the ACE model but inferior to that of the AE model for H and T in all regions except for T in right middle frontal gyrus. Model goodness-of-fit did not change significantly when D was omitted from the model (ADE vs. AE). However, the goodness-of-fit decreased with omission both A and D, further confirming a genetic influence (additive and/or dominant) on the amplitude and latency of the hemodynamic response (Table 3).

Table 3.

Statistical modeling of hemodynamic response function characteristics estimated with a fixed neuronal activity function^a.

HRFs	Model fit										Model comparison
	ACE		ADE		CE		AE		E		ACE vs. AE		ACE vs. CE		ADE vs. AE		ADE vs. E		AE vs. E
	−2LL	AIC	−2LL	AIC	−2LL	AIC	−2LL	AIC	−2LL	AIC	Δχ2	P	Δχ2	P	Δχ2	P	Δχ2	P	Δχ2	P
L-MFG-H	761.49	−158.51	761.10	−158.90	765.50	−156.50	761.49	−160.51	777.42	−146.58	0.00	1	4.00	0.04	0.39	0.53	16.32	2.85E–04	15.93	6.57E–05
L-SMG-H	403.03	−264.97	402.96	−265.04	404.54	−265.46	403.03	−266.97	410.75	−261.25	0.00	1	1.51	0.22	0.08	0.78	7.79	0.02	7.72	5.47E–03
L-AG-H	723.84	−54.15	723.45	−54.55	726.22	−53.78	723.84	−56.15	732.57	−49.43	0.00	1	2.37	0.12	0.39	0.53	9.12	0.01	8.72	3.14E–03
R-MFG-H	713.04	−238.96	709.69	−242.31	718.71	−235.29	713.03	−240.96	724.26	−231.74	0.00	1	5.67	0.02	3.34	0.07	14.57	6.87E–04	11.22	8.07E–04
R-SMG-H	461.48	−316.52	460.44	−317.56	464.88	−315.12	461.48	−318.52	472.30	−309.70	0.00	1	3.40	0.06	1.04	0.31	11.86	2.66E–03	10.82	1.00E–03
R-AG-H	505.15	−330.85	502.03	−333.97	511.60	−326.40	505.15	−332.85	518.96	−321.04	0.00	1	6.45	0.01	3.12	0.08	16.93	2.11E–04	13.81	2.02E–04
L-MFG-T	1403.89	483.89	1403.88	483.88	1406.17	484.17	1403.89	482.89	1419.67	495.67	0.00	1	2.28	0.13	4.59E–03	0.95	15.79	3.72E–04	15.79	7.09E–05
L-SMG-T	1112.68	444.68	1111.78	443.78	1115.63	445.63	1112.68	442.68	1120.93	448.93	0.00	1	2.95	0.09	0.90	0.34	9.16	0.01	8.25	4.06E–03
L-AG-T	1301.32	523.32	1300.31	522.33	1303.92	523.92	1301.32	521.32	1308.25	526.25	0.00	1	2.60	0.11	0.99	0.32	7.92	0.02	6.93	8.48E–03
R-MFG-T	1536.88	584.88	1535.30	583.30	1540.72	586.72	1538.88	582.88	1546.94	590.94	0.00	1	3.84	0.05	1.58	0.21	11.64	2.97E–03	10.06	1.51E–03
R-SMG-T	1412.07	634.07	1411.49	633.49	1416.13	636.13	1412.07	632.07	1424.33	642.33	0.00	1	4.07	0.04	0.57	0.45	12.84	1.63E–03	12.26	4.61E–04
R-AG-T	1504.21	668.21	1500.99	664.99	1507.44	669.44	1504.21	666.21	1509.69	669.69	0.00	1	3.23	0.07	3.22	0.07	8.71	0.01	5.481	1.91E–02
L-MFG-W	1382.74	462.74	1382.34	462.34	1383.51	461.51	1382.74	460.74	1384.63	460.63	0.00	1	0.78	0.38	0.40	0.53	2.29	0.32	1.89	0.17
L-SMG-W	1016.31	348.31	1014.22	346.22	1018.43	348.43	1016.31	346.31	1019.53	347.53	0.00	1	2.12	0.15	2.09	0.15	5.31	0.07	3.21	0.07
L-AG-W	1217.83	439.83	1215.59	437.59	1222.61	442.61	1217.83	437.83	1228.94	446.94	0.00	1	4.77	0.03	2.24	0.13	13.35	1.25E–03	11.11	8.58E–04
R-MFG-W	1587.08	635.08	1587.06	635.06	1588.76	634.76	1587.08	633.08	1597.72	641.72	0.00	1	1.68	0.19	0.03	0.87	10.66	4.83E–03	10.64	1.11E–03
R-SMG-W	1405.65	627.65	1405.58	627.58	1406.21	626.21	1405.65	625.65	1408.14	626.14	0.00	1	0.56	0.45	0.07	0.79	2.56	0.28	2.49	0.02
R-AG-W	1520.72	684.72	1517.82	681.82	1522.93	684.93	1520.72	682.72	1524.17	684.17	0.00	1	2.21	0.14	2.90	0.09	6.35	0.04	3.45	0.06

Note that the P values are conservative with the assumption of standard chi-square distribution. Given a null distribution of parameterized variance component being a 50/50% mixture of a χ²(0) and χ²(1) (Dominicus et al., 2006), the P values should be half of the values reported in this table.

^aHRFs are hemodynamic response function characteristics estimated with a fixed neuronal activity function. L-: left; R-: right; MFG: middle frontal gyrus; SMG: supramarginal gyrus; AG: angular gyrus; H: height; T: time to peak; W: full width at half maximum of the HRF; A: additive genetic factors; C: common environmental factors; D: dominance genetic factors; E: unique environmental factors (E); −2LL: minus 2 × log-likelihood; AIC: Akaike Information Criterion; Δχ²: change in chi-square; P: unadjusted P values; aEb: a × 10^b.

Simulation of HRF modeling with flexible neuronal activity function

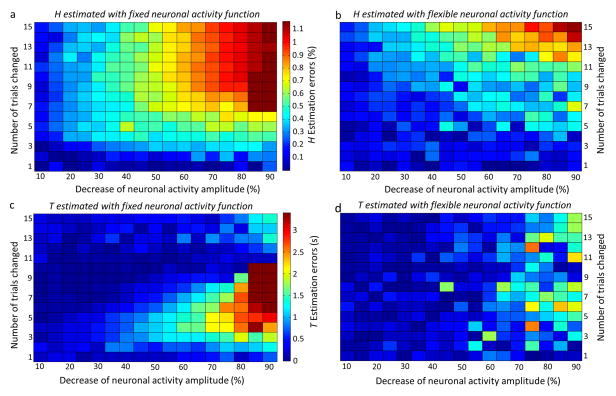
Estimation errors of HRF characteristics without noise are summarized in pseudocolor maps (Fig. 2). Use of a fixed neuronal activity function results in estimation errors for H if the actual neuronal activity does not follow the fixed function whereas errors in the estimation of T are not seen if the change in the amplitude of actual neuronal activity is less than 50%. HRF modeling with a flexible neuronal activity function improved the accuracy of HRF estimation when neuronal activity varied.

Fig. 2.

Pseudocolor plots of the estimation errors of HRF characteristics H (a, b) and T (c, d). The amplitude of the neuronal activity function was decreased in 5% increments between 10% and 90% of activity (represented by the horizontal axis). The number of trials in each block affected by the change in amplitude was varied from the first trial in each block to the first 15 of a total of 16 trials in each block (represented by the vertical axis). The absolute differences between the estimated HRF characteristics and the true values were color-coded: the color bars represent estimation errors in H between 0 and 1.2% (a and b) and in T between 0 s and 3.4 s (c and d). (a) and (c) respectively represent the estimation errors of HRF H and T using the fixed neuronal activity function. (b) and (d) respectively represent the estimation errors of HRF H and T using the flexible neuronal activity function. Overall, HRF H and T are estimated more accurately when a flexible as opposed to a fixed neuronal activity function is used. While HRF modeling with a flexible neuronal activity function improved the accuracy of HRF estimation when neuronal activity varied, errors in the estimation of T are not seen if the change in the amplitude of actual neuronal activity is less than 50%.

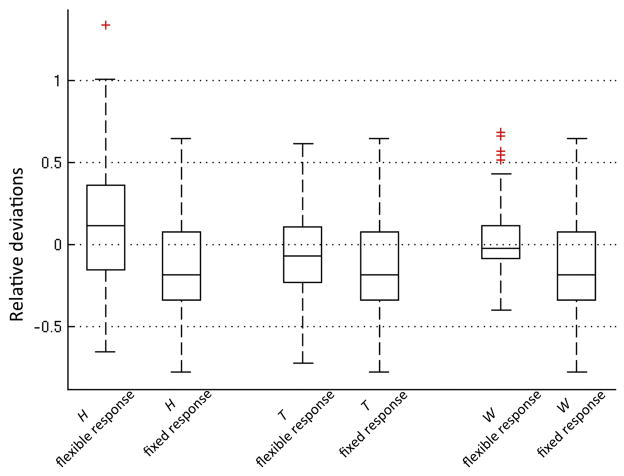
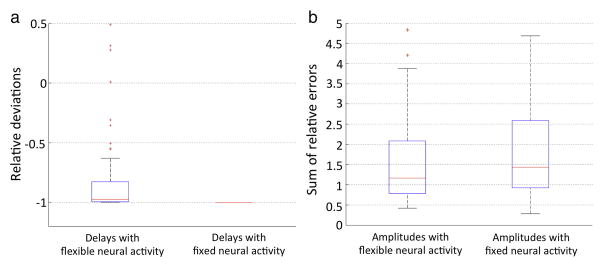
With random noise (temporal SNR = 150), H and T were estimated more accurately with a flexible neuronal activity function than with a fixed neuronal activity function (Fig. 3). As expected, the flexible neuronal activity function estimated the time course of neuronal activity more accurately than the fixed neuronal activity function (Fig. 4).

Fig. 3.

Box-and-whisker plot comparing the relative deviations of estimated HRF characteristics from the true values when flexible versus fixed neuronal activity functions were used. Outliers (red cross) were defined as exceeding 3 times the standard deviation; all data, including outliers without Winsorization, were considered in the analysis. The HRF characteristics estimated with the flexible neuronal activity function are more accurate (less deviation from the true values and smaller interquartile range) than those estimated using a fixed neuronal activity function.

Fig. 4.

Box-and-whisker plot of deviations of estimated neuronal activity from true values in the simulation study. Outliers (red cross) were defined as exceeding 3 times the standard deviation; all data, including outliers without Winsorization, were considered in the analysis. (a) The relative deviations of estimated delays in onset of neuronal activity from true values. (b) The sum of relative errors in estimated amplitude of neuronal activity. The delay and amplitude of neuronal activity estimated with the flexible neuronal activity function are more accurate than those estimated using a fixed neuronal activity function.

Correlations between estimated HRF characteristics, neuronal activation, and performance data

Several HRF characteristics were significantly correlated with task performance when a fixed neuronal activity function was used. HRF H in the L-MFG and L-AG was negatively correlated with performance accuracy, with both having a Pearson correlation coefficient (ρ) equal to − 0.11 (FDR-q < 0.05 and for all correlations reported below). The HRF H was positively correlated with response time in L-MFG (ρ = 0.13), L-SMG (ρ = 0.12), L-AG (ρ = 0.17), and R-AG (ρ = 0.13). No significant correlation was found between HRF characteristics and task performance when a flexible neuronal activity function was used.

There were no significant correlations between the estimated neuronal activity delays and performance data. Median of neuronal activity amplitude changes in L-MFG (ρ = −0.07), R-MFG (ρ = −0.06), L-SMG (ρ = −0.09), and R-SMG (ρ = −0.12) were negatively correlated with response accuracy. Median neuronal activity amplitude changes in L-MFG (ρ = 0.11) and L-AG (ρ = 0.07) were positively correlated with response time. The ApEns of neuronal activity estimated from the L-MFG (ρ = −0.08) and R-AG (ρ = −0.07) were negatively correlated with response accuracy. The ApEn of neuronal activity estimated from the L-MFG (ρ = 0.08) was positively correlated with response time.

Heritability of HRF characteristics modeled with flexible neuronal activity function

When the flexible neuronal activity function was used, the ICCs for H and T in MZ twin pairs were similar to those modeled with the fixed neuronal activity function (Table 2) and the findings from structural equation modeling showed a similar genetic influence on H and T (Fig. 1d and Table 4). The ICCs for median amplitude and approximate entropy of the estimated neuronal function in both MZ and DZ twin pairs were not significant and no significant genetic contribution was observed with structural equation modeling.

Table 4.

Statistical modeling of hemodynamic response function characteristics estimated with a flexible neuronal activity function^a.

HRFs	Model fit										Model comparison
	ACE		ADE		CE		AE		E		ACE vs. AE		ACE vs. CE		ADE vs. AE		ADE vs. E		AE vs. E
	−2LL	AIC	−2LL	AIC	−2LL	AIC	−2LL	AIC	−2LL	AIC	Δχ2	P	Δχ2	P	Δχ2	P	Δχ2	P	Δχ2	P
L-MFG-H	752.68	−159.32	752.64	−159.36	755.40	−158.60	752.68	−161.32	768.47	−147.53	0.00	1	2.72	0.10	0.04	0.84	15.83	3.64E–04	15.79	7.06E–05
L-SMG-H	498.34	−177.66	496.80	−179.20	501.77	−176.23	498.34	−179.66	505.80	−174.19	0.00	1	3.43	0.06	1.53	0.21	9.00	0.01	7.47	6.29E–03
L-AG-H	639.96	−122.04	640.60	−121.40	641.77	−122.23	640.60	−123.40	668.21	−97.79	0.64	0.43	1.81	0.18	0	1	27.61	1.01E–06	27.61	1.48E–07
R-MFG-H	763.56	−202.44	763.30	−202.70	767.32	−200.68	763.56	−204.44	779.76	−190.24	0.00	1	3.76	0.05	0.27	0.61	16.46	2.67E–04	16.19	5.72E–05
R-SMG-H	524.44	−293.56	524.25	−293.75	526.21	−293.79	524.44	−295.56	532.68	−289.32	0.00	1	1.77	0.18	0.19	0.66	8.44	0.01	8.24	4.09E–03
R-AG-H	693.44	−174.56	692.18	−175.82	696.41	−173.59	693.44	−176.56	700.67	−171.33	0.00	1	2.96	0.08	1.26	0.26	8.50	0.01	7.23	7.16E–03
L-MFG-T	1393.85	481.85	1393.85	481.85	1396.60	482.60	1393.85	479.85	1411.55	495.55	0.00	1	2.75	0.10	7.84E–03	0.93	17.70	1.43E–04	17.69	2.60E–05
L-SMG-T	1173.10	497.10	1171.58	495.58	1174.98	496.98	1173.10	495.10	1176.49	496.49	0.00	1	1.88	0.17	1.52	0.22	4.91	0.09	3.39	0.06
L-AG-T	1278.24	516.24	1277.67	515.67	1280.79	516.79	1278.24	514.24	1286.79	520.79	0.00	1	2.55	0.11	0.57	0.45	9.12	0.01	8.55	3.46E–03
R-MFG-T	1574.03	608.03	1570.83	604.83	1579.33	611.30	1574.03	606.03	1585.08	615.08	0.00	1	5.27	0.02	3.21	0.07	14.25	8.04E–04	11.04	8.89E–04
R-SMG-T	1421.73	603.73	1420.43	602.43	1423.79	603.79	1421.73	601.73	1425.88	603.88	0.00	1	2.06	0.15	1.30	0.25	5.46	0.06	4.16	0.04
R-AG-T	1487.34	619.34	1485.87	617.87	1490.88	620.88	1487.34	617.34	1496.08	624.08	0.00	1	3.55	0.05	1.47	0.22	10.21	6.05E–03	8.74	3.11E–03
L-MFG-W	1362.60	450.60	1362.53	450.53	1363.72	449.72	1362.60	449.60	1369.14	453.14	0.00	1	1.12	0.29	0.07	0.80	6.61	0.04	6.54	0.01
L-SMG-W	1117.20	441.20	1117.16	441.16	1117.25	439.25	1117.20	439.20	1117.26	437.26	0.00	1	0.04	0.83	0.04	0.83	0.01	0.95	0.06	0.80
L-AG-W	1217.47	455.48	1218.97	456.97	1217.48	453.48	1218.97	454.97	1222.14	456.14	1.50	0.22	0.00	1.00	0	1	3.17	0.20	3.17	0.07
R-MFG-W	1556.74	590.74	1556.77	590.77	1557.00	589.00	1556.77	588.77	1561.07	591.07	0.03	0.86	0.26	0.61	0	1	4.31	0.11	4.31	0.04
R-SMG-W	1437.64	619.64	1437.52	619.52	1437.86	617.86	1437.64	617.64	1438.11	616.11	0.00	1	0.21	0.64	0.01	0.73	0.06	0.74	0.47	0.49
R-AG-W	1483.78	615.78	1481.31	613.31	1487.28	617.28	1483.78	613.78	1489.78	617.78	0.00	1	3.50	0.06	2.47	0.12	8.47	0.01	6.00	0.01

Note that the P values are conservative with the assumption of standard chi-square distribution. Given a null distribution of parameterized variance component being a 50/50% mixture of a χ²(0) and χ²(1) (Dominicus et al., 2006), the P values should be half of the values reported in this table.

^aHRFs are hemodynamic response function characteristics estimated with a flexible neuronal activity function. L-: left; R-: right; MFG: middle frontal gyrus; SMG: supramarginal gyrus; AG: angular gyrus; H: height; T: time to peak; W: full width at half maximum of the HRF; A: additive genetic factors; C: common environmental factors; D: dominance genetic factors; E: unique environmental factors (E); −2LL: minus 2 × log-likelihood; AIC: Akaike information criterion; Δχ2: change in chi-square; P: unadjusted P values; aEb: a × 10^b.

Discussion

By comparing resemblance of HRF characteristics within MZ and DZ twin pairs, we have provided evidence for a significant genetic influence on the regulation of regional cerebral blood flow. The HRF was modeled by fitting the convolution of the HRF with the neuronal activity function to the fMRI time course. In most fMRI analyses, a fixed neuronal activity function, which assumes that the neuronal activity is the same as the time course of the stimuli presented in the experiments, is used. However, to test whether the observed heritability of HRF characteristics was due to the assumed time course of neuronal activity, we also used a flexible neuronal activity function to model the time course of the fMRI signal, fitting its convolution with the HRF to the fMRI time course to estimate both the HRF and neuronal activity. In simulation studies, the flexible neuronal activity function improves the accuracy of HRF estimation when the neuronal response to stimuli varies. Poorer performance (lower accuracy and longer mean response times) was associated with higher amplitude and more irregular neuronal activity. The relationship between HRF characteristics and performance differed between flexible and fixed neuronal activity functions in a manner consistent with the former being a more accurate representation of neuronal activity. This suggests that inaccurate representation of neuronal activity affects the estimation of HRF characteristics. In contrast, estimated HRF characteristics did not correlate with performance when the flexible neuronal activity function was used. The median amplitude change and approximate entropy, a measure of the temporal regularity of a signal (Pincus, 1991), of the neuronal activity function correlated with in-scanner subject performance providing support for the flexible neuronal activity function as an accurate representation of neuronal activity. The genetic influence on HRF characteristics was similar for fixed and flexible neuronal activity functions. Hence we conclude that the observed heritability reflects genetic influences on regional blood flow regulation per se rather than an effect mediated via neuronal activity.

Based on our sensitivity analyses of fMRI signal physiological determinants with the generalized Balloon Model (Buxton et al., 2004; Stephan et al., 2007) (Supplementary Fig. S1 and Table S1), we believe that the heritability in HRF amplitude found here is most likely attributable to genes regulating vasodilator signaling or blood vessel stiffness. Candidate genes include those involved in synthesis of vasodilators such as nitric oxide synthase 1 (NOS1) and cyclooxygenase (COX). Indomethacin, a cyclooxygenase inhibitor, has been shown to decrease the blood oxygenation level-dependent response in fMRI (Bruhn et al., 2001). Furthermore, the amplitude of the HRF is affected by COX genotypes (Hahn et al., 2011). Heritability for vascular compliance has been demonstrated for the venous system in which heritability is about 90% (Brinsuk et al., 2004). Here, genes for vessel wall proteins such as desmuslin, an intermediate filament protein in the smooth muscle cell wall (Anwar et al., 2012), may be important genetic influences on blood vessel stiffness. We demonstrated a significant genetic contribution to individual variation in T and have previously shown that H and T can be estimated accurately and independently (Shan et al., 2014). Our sensitivity analyses showed that T is most strongly influenced by neurovascular coupling delay, reflecting the influence of genes involved in vascular signaling.

Significant resemblance in W in MZ twins was observed for estimates made with a fixed but not a flexible neuronal activity function suggesting that some of the observed heritability in the former was due to similarity in the time course of neuronal activity within MZ twin pairs. W is only moderately reproducible (Shan et al., 2014), imposing a ceiling on estimates of heritability. In light of these two observations, the present data do not allow us to conclude that there are significant genetic influences on W.

In the current study, the HRF was estimated from block design fMRI data. Paradigm design was an unavoidable limitation of the retrospective analysis of fMRI data that had originally been collected to study the heritability of spatial patterns of functional activation with a working memory task (Blokland et al., 2011). We note that block designs are not optimal for HRF estimation and that random event-related designs and m-sequence designs have higher estimation efficiency (Maus et al., 2012). However, in our previous work, we demonstrated that HRF parameters can still be reliably estimated from block design fMRI data (Shan et al., 2014).

Our findings indicate that genetic factors contribute to individual variability in the coupling of the hemodynamic response to neuronal activity. The findings identify a new potential contributor to the heritability of some neurological diseases. The HRF may be a bridge between genes and diseases such as small vessel disease, a major cause of cognitive decline and gait disability with aging, in which altered neurovascular coupling has recently been implicated as playing a central pathobiological role (Gorelick et al., 2011; Iadecola, 2013; Zacchigna et al., 2008). A growing literature also implicates abnormal neurovascular mechanisms in the development and progression of Alzheimer’s disease. Vascular insufficiency activates the cleavage of the amyloid precursor protein (Kitaguchi et al., 2009) and promotes amyloid formation (Okamoto et al., 2012) and tau phosphorylation (Koike et al., 2010) in Alzheimer’s disease and preliminary evidence suggests that control of vascular risk factors may delay the progression of the disorder (Deschaintre et al., 2009; Richard et al., 2010).

Appendix A. Supplementary data

Supplementary data to this article can be found online at http://dx.doi.org/10.1016/j.neuroimage.2015.09.016.