Fig. 9.

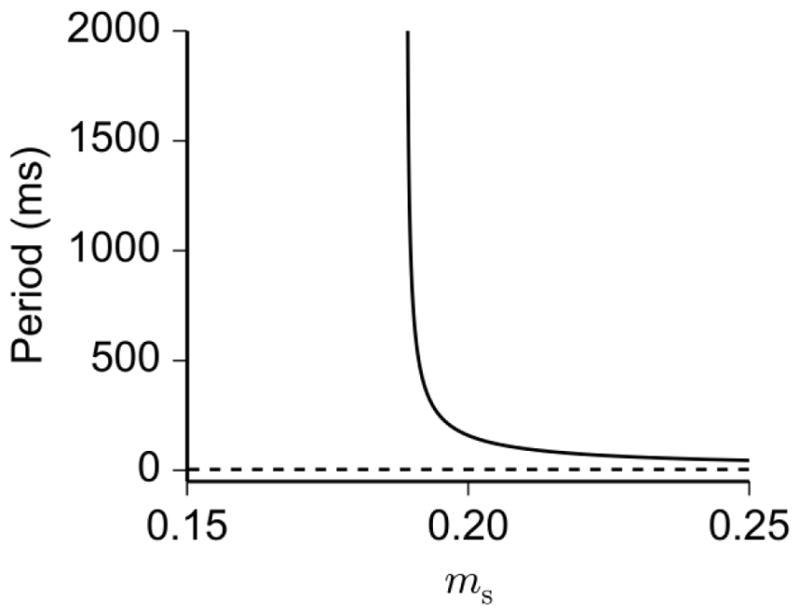
Dependence of slow variable m_s (treated as a parameter) on the period of limit cycles in the fast subsystem. The period of stable (solid) and unstable (dashed) limit cycles is plotted against m_s. Stable limit cycles represent spiking solutions of the fast subsystem. The other slow variables (h_2,HVA and Ca) are fixed at the values they attain at t = 3 s in the burst cycle of Fig. 8a. Notice that the period of the stable limit cycle is a decreasing function of m_s, indicating a decrease in interspike interval as m_s approaches its peak value during the burst. The blow-up in period shows the existence of a homoclinic (HC) bifurcation