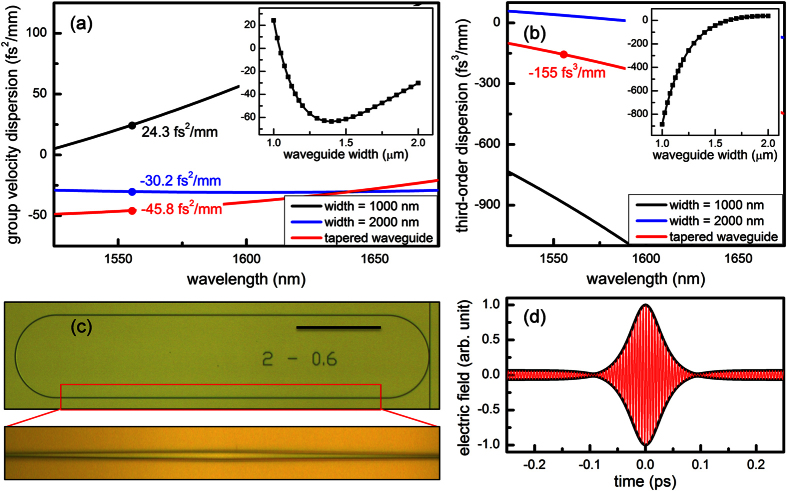
Figure 2. Design of the novel single-mode microresonator.

(a,b) Group velocity dispersion and third-order dispersion of the uniform waveguides with different widths and the tapered waveguide calculated with a commercial full-vector finite-element-mode solver (COMSOL Multiphysic), taking into consideration both the waveguide dimensions and the material dispersion³⁸. To account for the tapered geometry, waveguide dispersions are calculated for various widths (1 to 1.2 μm with a step of 25 nm and 1.25 to 2 μm with a step of 50 nm) and dispersions as a function of waveguide width is obtained using a cubic spline interpolation (insets). The fitted functions are then used to calculate the path-averaged dispersions 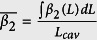and 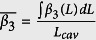, where dL = 400nm. (c) An optical micrograph of the designed single-mode microresonator. The waveguide in the semi-circle regions has a uniform width of 1 μm, supporting only the fundamental modes. On the other hand, the 800 μm long straight waveguide has a tapered width from 1 μm at the end to 2 μm at the middle of the waveguide. The total cavity length is 2.2 mm. Scale bar: 200 μm. (d) Dissipative cavity soliton with a FWHM duration of 50 fs is obtained by numerically solving the Lugiato-Lefever equation (LLE),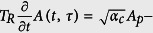 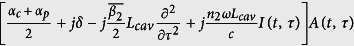, where A(t, τ) is the envelope function of the dissipative cavity soliton, α_p is the propagation loss, α_c is the coupling loss, δ is the pump-resonance detuning, and T_R is the cavity roundtrip time. 2,001 modes centered at the pump are incorporated in the LLE modeling. The simulation starts from vacuum noise and is run for 1.5 × 10⁵ roundtrips until the solution reaches the steady state.