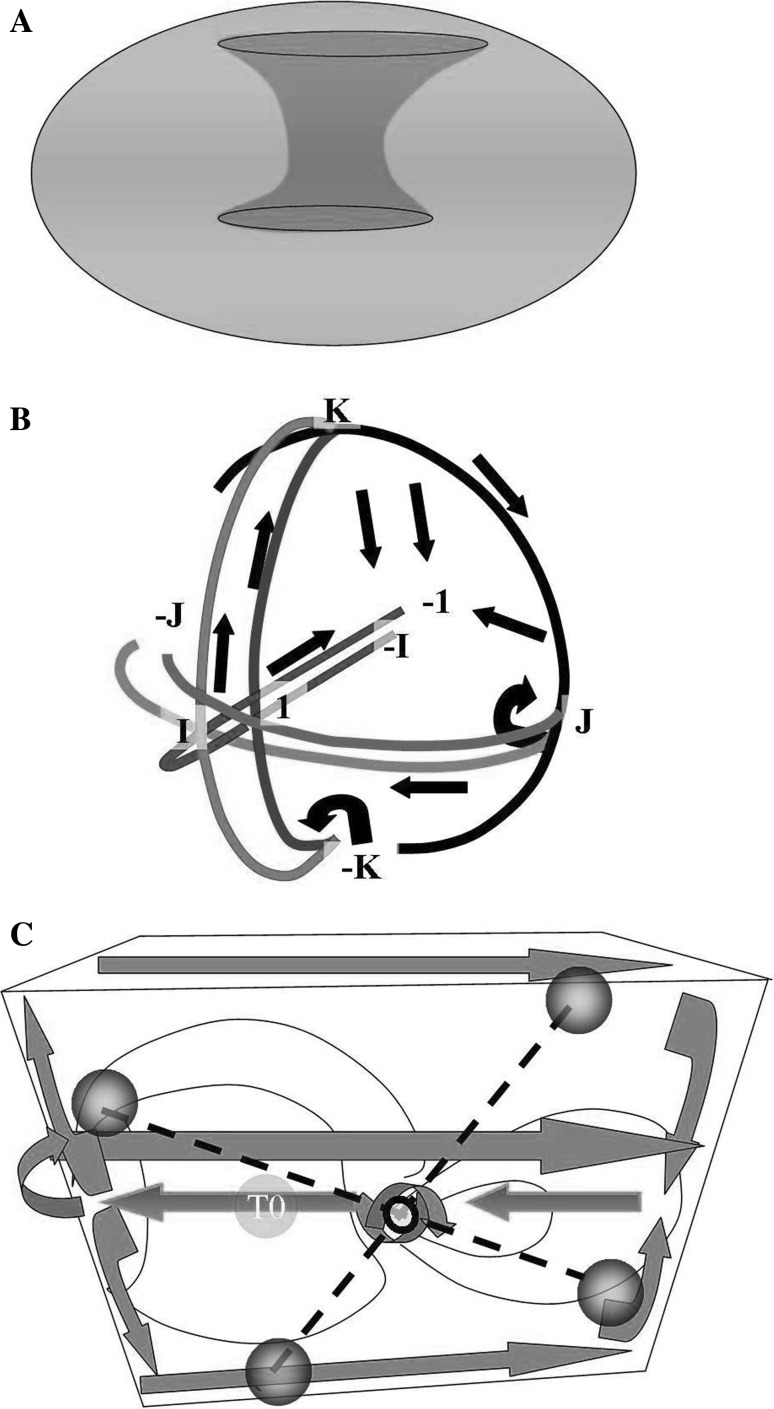
Fig. 1.

Different ways to depict a hypersphere. a How two 2-spheres glued together along their spherical boundary give rise to a donut-shaped Clifford torus. b Another way to depict a hypersphere: the superimposition of two 2-spheres (which circumferences are glued together) gives rise to a glome. Some of the quaternion rotations are depicted by the straight and curved arrows. c 3D projection of a hypersphere. The lines on the left enlarge in diameter, forming a circle of increasing circumference on the left surface of the 3D space. Conversely, on the opposite right side, the lines shrink and give rise to a circle of decreasing circumference on the right surface of the 3D space. See text for further details. The dotted lines and the black spheres depict some of the possible antipodal points predicted by the Borsuk Ulam Theorem (to give another example, J and −J are antipodal points in a)