Figure 1.

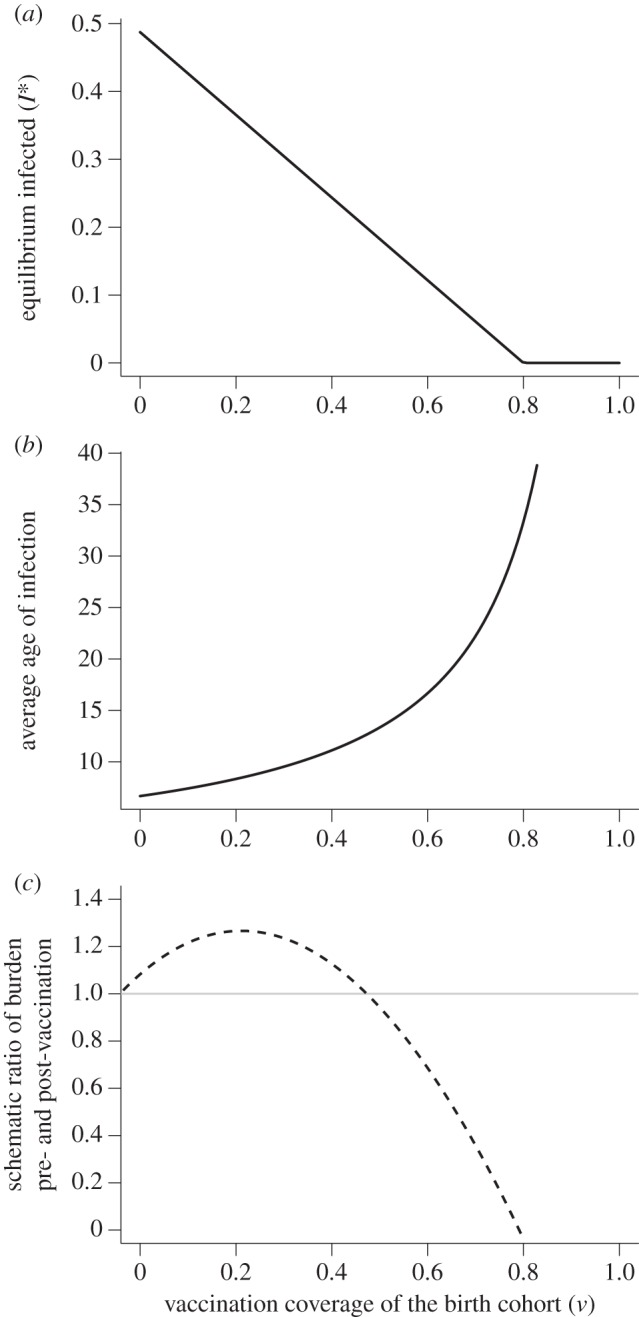
Theoretical expectations for RCV coverage and the burden of CRS. In a classic SIR framework, the dynamics of susceptibles are captured by dS/dt = μ(1 − v) − βSI − μS; and infected by dI/dt = βSI − gI − μI; where μ is the birth and death rate, total population size as taken as N = 1, v is vaccination coverage of the birth cohort, g is the generation time of the infection and the transmission rate is β = R₀(g + μ). To capture rubella dynamics, we set g to 18 days⁻¹, R₀ = 5, and chose μ = 30 per 1000 per year. (a) The equilibrium proportion of infected individuals I* (y-axis) is defined by I* = μ[(1 − v)R₀ − 1]/β and thus declines with increasing vaccination coverage (x-axis). (b) Conversely, the average age of infection A (y-axis) increases, following R₀ = G/A, where G is the inverse of the unvaccinated birth rate, G = 1/[μ(1 − v)]. (c) This conjunction of declining incidence but increasing average age of infection has the potential to yield a situation where more cases are occurring in women of childbearing age, even though the total number of cases is declining. As a result, the ratio of the equilibrium burden of CRS in the presence of vaccination relative to the equilibrium burden of CRS if no vaccination has occurred (y-axis) may first increase with vaccination coverage relative to the scenario of no vaccination (indicated by the horizontal grey line); eventually declining when incidence is sufficiently low to offset the increase in the average age of infection. (Results in the last panel are hypothetical; exact values will depend on the variance and skew of the distribution of age of infection; as well as pattern of fertility over age). This pattern of increasing CRS burden with increasing vaccination coverage has been called ‘the paradoxical increase of rubella’.