Figure 3.

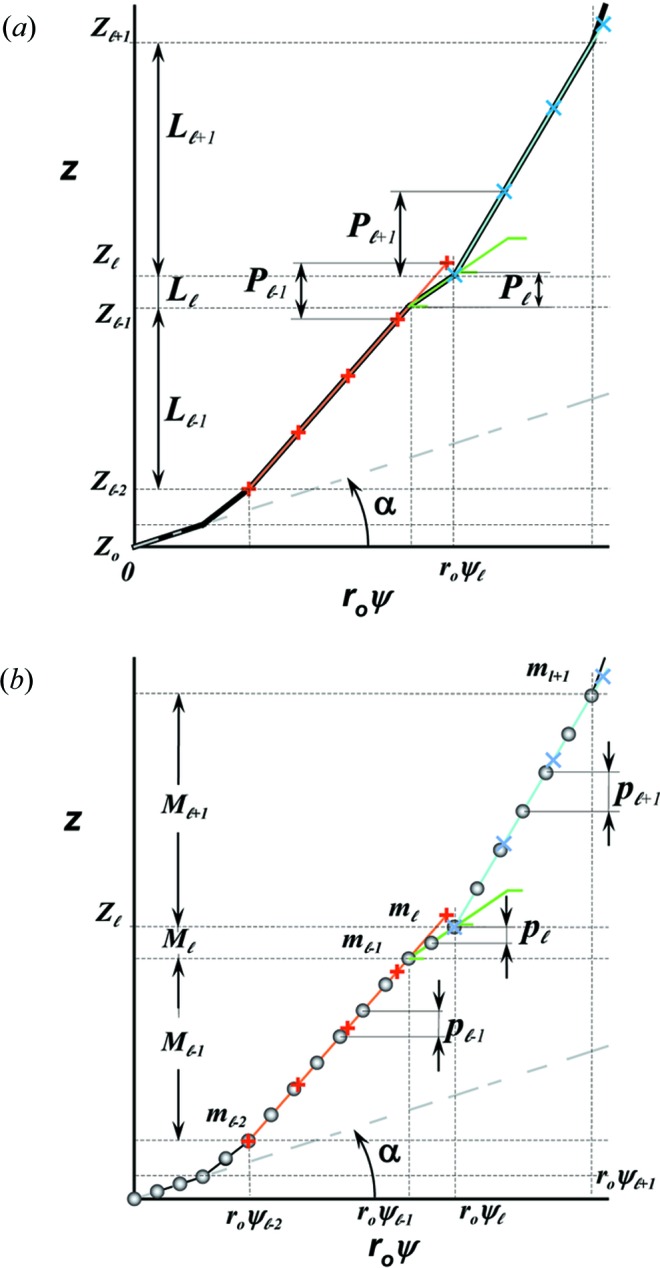
Stretched helical structures in terms of a radial projection. The undeformed helix from Fig. 1 ▸(a) is represented in a radial projection as a straight line inclined at an angle α (gray dashed lines) and, similarly, the undeformed helical strands of subunits from Fig. 1 ▸(b) form a radial net of points along the same straight line (Squire & Knupp, 2005 ▸). However, the deformed helix with piecewise changes in the inter-subunit spacings shows changes in slope in the radial projection, i.e. the change in spacings modulates the angle α between the points where the spacing changes, but maintains straight lines between the points where the slope does not change. The change in slope also modulates the pitch, P. (a) A continuous helix with spacing changes for the first 21 actin monomers from Fig. 2 ▸. The changes in spacings are defined at 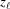and ψ_ℓ or r ₀ψ_ℓ in the radial projection. The length of constant pitch segments is defined as L _ℓ = z _ℓ − z _ℓ−1, where the index ℓ denotes the current number of the segment with the constant pitch P _ℓ. The first point of the helix is set to be at z ₀ = 0 and ψ₀ = 0. The index of the coordinate of each segment end point, i.e. the coordinate where the slope changes, is set to coincide with the current segment number ℓ. Three consecutive segments with constant pitches are illustrated by light-red, green and cyan lines, and the points along these line segments indicating one complete pitch with red crosses, green horizontal ticks and light-blue crosses, respectively. (b) The subunits, depicted as gray spheres, follow the segment slopes from part (a). The index of each subunit is denoted as m. The subunit number at position 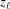is denoted 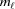and the subunit spacing within the segment as 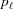. Note that the length of the segment 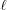is shorter than one pitch, i.e. 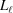= 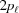< 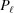. The number of spacings in the segment 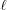is denoted .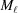