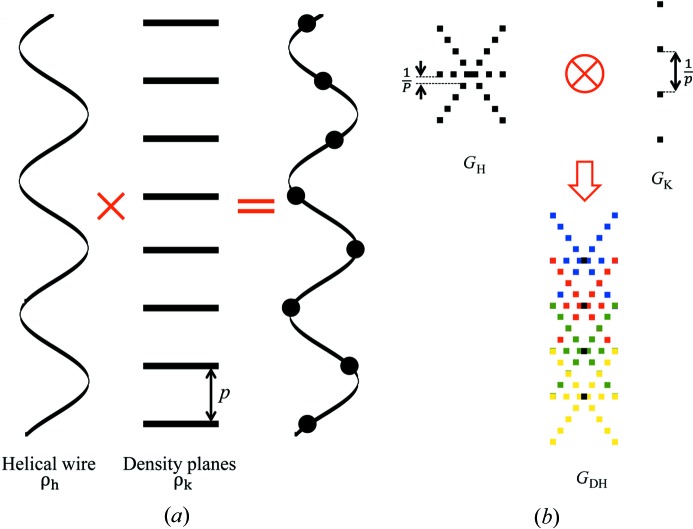
Figure 4.

Generation of the discontinuous helix and its diffraction pattern. (a) A discontinuous helix (i.e. a helical array of subunits) can be thought of as a product of a helical wire, ρ_h, with a set of horizontal planes, ρ_k, spaced p apart, where p is the subunit axial translation. (b) The Fourier transform of the discontinuous helix, G _DH, is represented as the convolution of the Fourier transforms of objects ρ_h and ρ_k, denoted G _H and G _K, respectively. Graphically, this convolution is represented as a series of overlapping G _H patterns, each originating at the meridional reflection positions, separated by 1/p, described by G _K (Vainshtein, 1966 ▸; Squire, 1981 ▸).