Fig. 1.

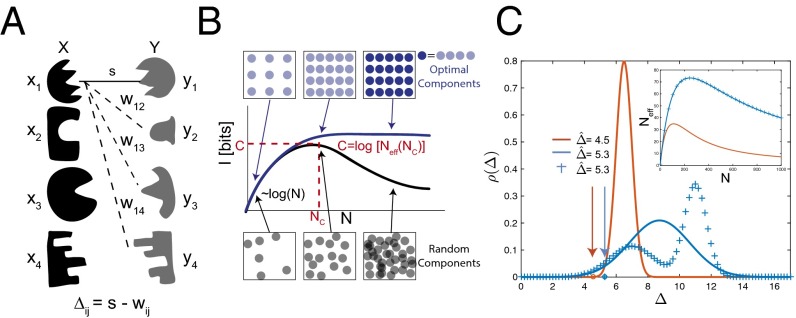
Information theory determines the capacity of systems of specific interactions. (A) A model system of locks (black) that each bind with energy s to their specific key (gray) via some specific interaction. (B) As the number N of lock–key pairs is increased, noncognate locks and keys inevitably start resembling each other as they fill up the finite space of all possible components (boxes), both with optimized or random design of lock–key pairs (circles). Consequently, mutual information I between bound locks and keys rises with N for small N but reaches a point of diminishing returns at $N=N_C$; due to the rapid rise in off-target binding energy, I can no longer increase and, for randomly chosen pairs, will typically decrease. The largest achievable value of I is the capacity C. (C) Capacity C can be estimated from the distribution $\rho \left(\mathrm{\Delta }\right)$ of the gap $\mathrm{\Delta }=w-s$ between off-target binding energy w and on-target binding energy s for randomly generated lock–key pairs. Among the three distinct $\rho \left(\mathrm{\Delta }\right)$ shown, the blue distributions have the same $\beta \widehat{\mathrm{\Delta }}=-\log {\langle \beta \mathrm{\Delta }{e}^{-\beta \mathrm{\Delta }}\rangle }_{\rho }$. (C, Inset) $I\left(N\right)$ (compare Eq. 3) is the same for the blue distributions that, despite being markedly different in shape, have the same $\widehat{\mathrm{\Delta }}$, which captures the essential aspects of crosstalk.