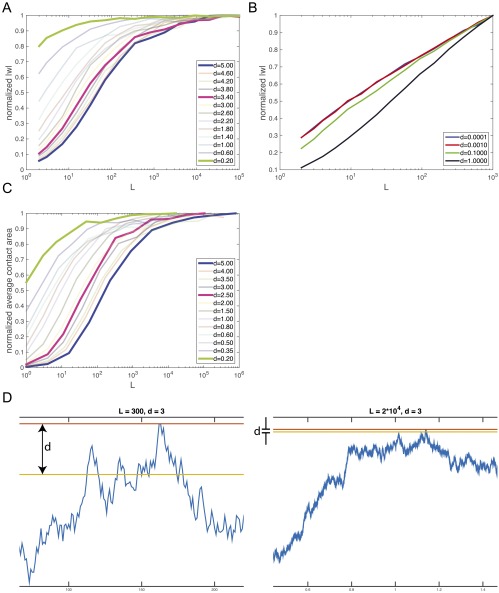
Fig. S4.

(A) We measure the average off-target energy $\left|w\right|$ for shaped components (of the form shown in Fig. 3A, main text) at various d and L. No translation is allowed between components. Each curve is normalized by its maximal value. As L increases, $\left|w\right|$ first increases sublinearly with L and then saturates. (B) The normalized $\left|w\right|$ for shaped components when translation is allowed. w for each pair is taken as the strongest possible binding across all translations. Each curve is normalized by its maximal value. As L increases, $\left|w\right|$ increases logarithmically with L. There does not appear to be saturation for the range of numerically achievable L. (C) Similarly, we measure the average amount of time a random 1D walk of L time steps spends within d of its maximum. As L becomes large with respect to d, the average time saturates. Each curve is normalized by its maximal value. (D) Two typical random walks of length 300 (Left) and 20,000 (Right). The amount of time that the random walk spends between its maximum (red line) and within $d=3$ of its maximum (yellow line) is a large fraction of the length for small L, but for very long walks is independent of L.