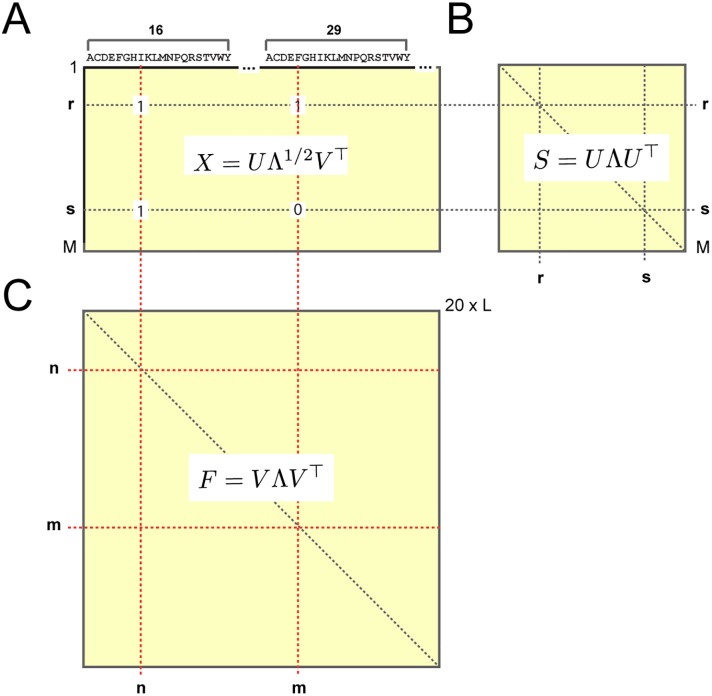
Fig 5. The mathematical relationship between sequence and positional correlations.
A, A binary matrix representation of the alignment Xsn, comprised of M sequences by 20 × L amino acids (Fig 1C); the equation shows the singular value decomposition (SVD) of X (Eq (12)). From the alignment matrix, two correlation matrices can be computed: S, a correlation matrix over rows (B) describing relationships between sequences, and F, a correlation matrix over columns (C) describing relationships between amino acids; equations show the eigenvalue decompositions of these matrices. By the SVD, X provides a mapping between the two such that the eigenvectors of F (in V) correspond to the eigenvectors of S (in U). Thus, it is possible to associate coevolving groups of amino acids to patterns of sequence divergence in the alignment. As described in the text, a similar mapping is possible for positional (rather than amino acid specific) coevolution (Eq (14)).