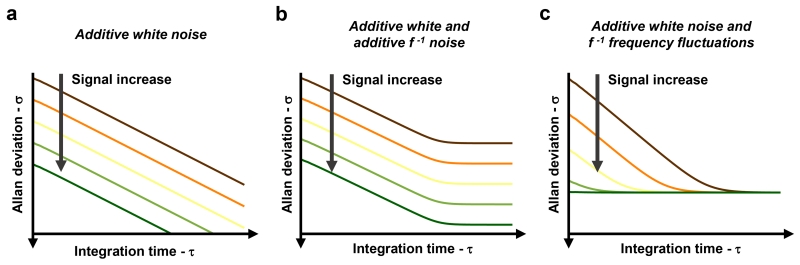
Figure 3. Additive phase noise and frequency fluctuations show different features in the Allan deviation.
Effect of different noise sources on the frequency stability as a function of the integration time τ, and for different signal levels. a, Additive white noise, manifesting itself as phase noise. It presents a constant slope of τ−½. The stability improves with increasing signal level. b, Combination of additive white and f−1 noises. For low integration times it presents a slope of τ−½, which becomes τ0 when the f−1 noise dominates at large integration times. The stability improves with increasing signal level in the whole time range. c, Combination of additive white noise with f−1 frequency-fluctuations. For low integration times it presents a slope of τ−½, which becomes τ0 when the f−1 frequency noise dominates. Moreover, the stability due to frequency fluctuations is insensitive to the signal level: therefore, an increase in the signal has an effect only when additive noise dominates.