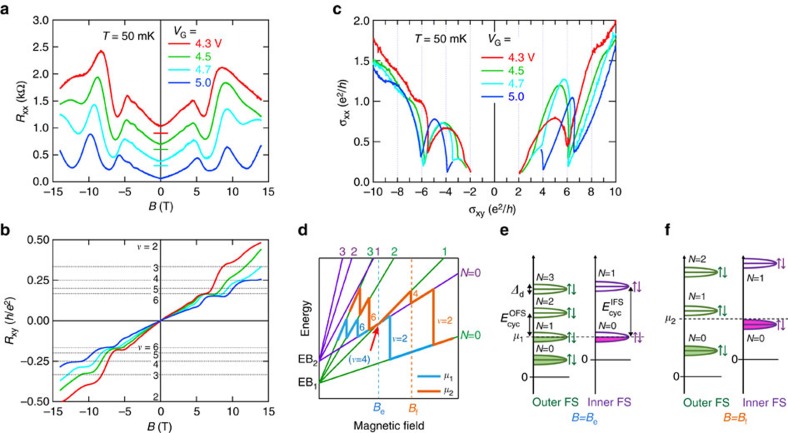
Figure 3. Carrier density dependence of quantum transport in δ-doped SrTiO₃.

(a,b) Longitudinal resistance R_xx (a) and Hall resistance R_xy (b) versus magnetic field B measured at 50 mK with various V_G's. For R_xx, the traces are shifted vertically for clarity as denoted by horizontal bars. Horizontal dotted lines in b are the Landau level filling factors (ν=2−6). (c) Parametric plots of (σ_xy(B), σ_xx(B)) for various gate voltages at 50 mK. (d) A schematic of Landau levels as a function of magnetic field. Green and purple lines correspond to the Landau levels (N) of outer (EB₁) and inner (EB₂) subbands, respectively. All lines contain up and down spin states, assuming spin degeneracy due to the small g-factor. The thick blue and orange lines illustrates the chemical potentials (μ₁ and μ₂) for low and high V_G's. If the chemical potential (blue line μ₁) is located at the crossing point of N=1 of the outer subband and N=0 of the inner subband (indicated by the arrow), then ν=4 is expected to vanish. Shifting the chemical potential upward away from this crossing point (exemplified by the orange line (μ₂)), ν=4 can appear. (e) Landau level arrangement when ν=4 disappears. Δ_d is the Landau level broadening. 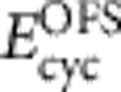and 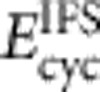are the cyclotron energies of the outer and inner FSs, respectively. Note that each Landau level N is spin degenerate. (f) Landau level arrangement when ν=4 can be observed.