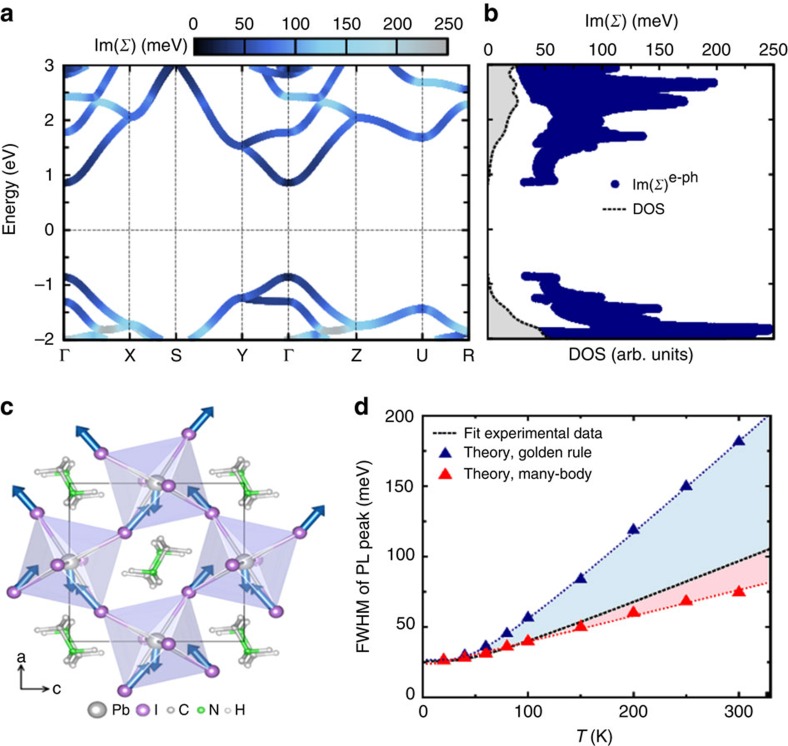
Figure 3. Ab initio calculations of electron–phonon coupling and PL broadening in MAPbI₃.

(a) Electronic band structure of orthorhombic MAPbI₃, calculated within the GW approximation as in ref. 55, combined with a heat map of the imaginary part of the electron–phonon self-energy (Im(Σ)) at T=200 K. The zero of the energy is placed in the middle of the bandgap. In b, the imaginary part of the electron–phonon self-energy is shown together with the electronic density of states (DOS). 2 Im(Σ) corresponds to the electron/hole linewidth arising from electron–phonon coupling (apart from the quasiparticle renormalization factor Z). (c) Ball-and-stick representation of the LO vibration responsible for the broadening of the PL peaks. The blue arrows indicate the displacements of Pb and I atoms, for the phonon wavevector q→0 along the [100] direction. This is a Pb–I stretching mode with B_3u symmetry⁵¹. (d) Temperature dependence of the FWHM of the PL peak in MAPbI₃: fit to the experimental data (dashed black line) and theoretical calculations using Fermi's golden rule (blue triangles) and the more accurate Brillouin–Wigner perturbation theory (red triangles). The theoretical broadening is obtained as the sum of 2 lm(Σ) at the valence and conduction band edges in the case of Fermi's golden rule, and the sum of 2 Z lm(Σ) when including many-body quasiparticle renormalization, rigidly shifted by the FWHM at T=0 K (25.72 meV), to account for inhomogenous broadening. The lines are guides to the eye.