Using Family Members to Augment Genetic Case-Control Studies of a Life-threatening Disease

Abstract

Survival bias is difficult to detect and adjust for in case-control genetic association studies but can invalidate findings when only surviving cases are studied and survival is associated with the genetic variants under study. Here, we propose a design where one genotypes genetically-informative family members (such as offspring, parents, and spouses) of deceased cases and incorporates that surrogate genetic information into a retrospective maximum likelihood analysis. We show that inclusion of genotype data from first-degree relatives permits unbiased estimation of genotype association parameters. We derive closed-form maximum likelihood estimates for association parameters under the widely used log-additive and dominant association models. Our proposed design not only permits a valid analysis but also enhances statistical power by augmenting the sample with indirectly studied individuals. Gene variants associated with poor prognosis can also be identified under this design. We provide simulation results to assess performance of the methods.

1. Introduction

In genetic association studies based on case-control data, many cases may not be available for genotyping only because they did not survive or they are too sick to participate. Such losses impose an ongoing challenge for research involving important debilitating or life-threatening conditions, because bias in inference, known as “survival bias” or healthy participant bias, will result if those losses are genetically informative. Survival bias, as one type of selection bias [1], has been recognized as a source of potential bias in many published genetic association studies (e.g., [2, 3, 4, 5]). It can also be a source of between-study heterogeneity in meta-analyses of genome-wide association studies [6], and may be responsible for failure to replicate some genetic association signals [7].

Current literature is sparse on study designs and statistical methods for addressing survival bias. Using simulation studies, Andersen et al. [7] evaluated the extent of bias by jointly modeling survival and association. The prospective study design was suggested as an unbiased alternative (e.g., [8]), but cohort studies are often infeasible. Alternatively, more stringent eligibility criteria can be applied to exclude some cases, e.g., based on recent diagnosis, (e.g., [9, 10]). But such constraints can lead to substantially reduced sample size and impose other kinds of selection that limit the generalizability of the study findings. Here, we develop a family-supplemented design (FSD) that permits correction and sensitivity analysis of survival bias in population-based case-control studies by genotyping family members. The central idea is that genotypes of family members of a deceased case can help provide information on the genotype of the deceased case, although the type of information depends on which family members are included. With our proposed strategy of genotyping cases and controls who are alive and also family members of representative deceased cases, we describe valid and efficient statistical methods for quantifying genetic associations both with disease and with survival given disease. We apply our method to a study of young-onset breast cancer where genotype data was available for slightly over half of the eligible case women by genotyping the available unaffected sister as a proxy for each unavailable case. We show that our method can greatly improve statistical power while simultaneously controlling healthy participant bias.

2. Method

We provide explanations for all notations in Section 6 Appendix Table 1 and Appendix Figure 1. We begin by considering only genetic effects. Let Y (coded as 1 or 0) denote case-control status. Suppose that among N₁ cases, n₁ have survived and provided genetic data. For simplicity of exposition, we assume that genetic data are available for one child, possibly together with that for the spouse (the other parent of that child), for each of the m= N₁−n₁ deceased cases, or for a random subset of them. The method we describe below can be readily extended to incorporate data from multiple offspring or a mix of available family structures that could include a variety of genetically informative first-degree relatives, e.g. some siblings or parents of deceased cases, in lieu of offspring.

Assume that we have genetic data for N₀ controls, who are representative of the control population (i.e., those not studied are missing at random, and if stratified sampling was used the analysis will also be stratified). We wish to study the association between Y and a di-allelic autosomal single nucleotide polymorphism (SNP), with major/minor alleles A/a. Let G_i denote the SNP genotype data for subject i, and let $G_i^f$ denote the genotype data of family members for the ith subject (only family members of deceased cases will be asked to provide genotype information). When one child (of the deceased case) and their spouse are accessible, $G_i^f=\left(G_i^c,G_i^p\right)$, where $G_i^c$ and $G_i^p$ denote their respective genotype data. When only one child or the spouse is accessible, $G_i^f=G_i^c$ or $G_i^f=G_i^p·G_i^f$ is coded as missing when no family member has been genotyped. We assume that a logistic regression model describes the association between Y and G:

$$p(Y=1\mid G)=\frac{e^{{\beta }_0+\beta f(G)}}{1+e^{{\beta }_0+\beta f(G)}},$$ (1)

where f(G) is a function of G that captures the penetrance model of interest, and β can be a vector. For example, for a co-dominant genetic model, f(G) is a vector with two indicator functions I_(G=1) and I_(G=2), and β = (β₁, β₂). For a log-additive model, f(G) would be the number of copies (0, 1, or 2) of the minor allele a. Let S coded as 1/0 indicate the survival of a case (where S = 1 if survived). We assume that cases with genotype g have survival probability q_g = p(S=1|G=g, Y=1). With a co-dominant model for survival, different probabilities, q₀, q₁ and q₂, are allowed, while q₁ and q₂ are equal when a dominant model is used.

When the genotype G is predictive of both risk of disease and survival given disease, one cannot assume that fitting model (1) with data from n₁ < N₁ cases and N₀ controls will yield unbiased estimates of the association parameter β. Under FSD, we consider that genotype data for one child, or the spouse (the child’s biological parent), or both can be made available for all or a random subset of the m deceased cases. We develop a maximum likelihood estimation (MLE) method for estimating the log odds ratio parameter β with genotype data for the N₀ controls and n₁ cases and genotype data for the family member(s) of the m deceased cases. We shall assume Mendelian inheritance and that the influence of the spouse genotype on risk is only through the implicit genetic information that the spouse and child genotypes provide about the missing genotype of the case and not through any mechanism related to genetic population structure, or effects of the variant on fertility or assortative mating. The likelihood for the observed data can be written as:

$$\prod _{i=1}^{N_1}\left\{{\left[p(S_i=1,G_i\mid Y_i=1)\right]}^{S_i}{\left[p(S_i=0,G_i^f\mid Y_i=1)\right]}^{1-S_i}\right\}\prod _{i=N_1+1}^{N_1+N_0}p(G_i\mid Y_i=0).$$ (2)

Note that for now we are assuming for simplicity that only survival of cases and not that of controls is related to the genotype at the studied locus. However, this likelihood (the right-hand product factor) could easily be expanded to include an effect of the variant genotype on survival in those without the disease.

We further assume that the child’s and spouse’s genotypes at the locus under study are not related to the case’s survival, conditional on the genotype of the case, i.e., $p(S_i=0\mid G_i,G_i^f,Y_i=1)=p(S_i=0\mid G_i,Y_i=1)$, and that the family members of cases whose genetic data are available are representative of case family members in the source population conditional on the case phenotype. Using a result from Satten and Kupper [11] to relate p(G|Y=1) to p(G|Y=0) for a rare outcome,

$$p(G\mid Y=1)=e^{\beta f(G)}p(G\mid Y=0)/{\sum }_{G=g}{e}^{\beta f(g)}p(G=g\mid Y=0),$$

and by partitioning according to the composite events and applying the assumed models, the log of the observed data likelihood function (2) for a rare phenotype can be rewritten as:

$$\begin{array}{l}\ell (\beta ,q,p_a)=\sum _{i=1}^{N_1}\left[S_{i}log\left\{p\left(S_i=1\mid G_i,Y=1\right)e^{\beta f(G)}p\left(G_i\mid Y=0\right)\right\}\right]\\ +\sum _{i=1}^{N_1}\left[\left(1-S_i\right)log\sum _{G=g}\left\{p\left(S_i=0\mid G=g,Y=1\right)e^{\beta f(g)}p\left(G=g,G_i^f\mid Y=0\right)\right\}\right]\\ -N_{1}log\left\{\sum _{G=g}{e}^{\beta f(g)}p\left(G=g\mid Y=0\right)\right\}+\sum _{i=N_1+1}^{N_1+N_0}log\left\{p\left(G_i\mid Y=0\right)\right\}.\end{array}$$ (3)

Under Hardy-Weinberg equilibrium (HWE), random mating, and Mendelian inheritance at the test locus in the population from which cases and controls arise, and assuming a rare phenotype, the probabilities p(G, G^f |Y=0) and p(G|G^f,Y=0) are functions of the MAF, p_a (Web Appendix 1). Let n₁₀, n₁₁, n₁₂ denote the respective numbers of living cases (the second index) with genotypes AA, Aa, and aa. Let m_jk denote the number of deceased cases whose child’s and spouse’s genotype data, G^c =j and G^p =k, is available, where j and k take values 0, 1, or 2 corresponding to genotypes AA, Aa, and aa, respectively. Note that not all combinations are possible; for example m₀₂ and m₂₀ cannot occur. Let m_jc denote the number of deceased cases whose child’s genotype G^c =j is available, while the spouse’s genotype data is not.

Define inverse probability weighted cell counts N̂₁₀ = n₁₀/q̂₀, N̂₁₁ = n₁₁/q̂₁, and N̂₁₂ + n₁₂/q̂₂, which can be seen as the predicted number of subjects with genotypes AA, Aa, and aa among the original total of N₁ case subjects. Note that, as one might hope, N̂₁₀ + N̂₁₁ + N̂₁₂ + N₁ (see Web Appendix). Under co-dominant coding for both association, f(G), and survival (to study) conditional on disease, we obtain the maximum likelihood estimated odds ratio (OR) association parameters as

$${\widehat{\beta }}_1=log\frac{{\widehat{N}}_{11}{\widehat{N}}_{00}}{{\widehat{N}}_{10}{\widehat{N}}_{01}}\text{and}{\widehat{\beta }}_2=log\frac{{\widehat{N}}_{12}{\widehat{N}}_{00}}{{\widehat{N}}_{10}{\widehat{N}}_{02}},$$

where N̂₀₀ = N₀(1−p̂_a)², N̂₀₁ = 2N₀p̂_a(1−p̂_a), and ${\widehat{N}}_{02}=N_0{\widehat{p}}_a^2$ are the expected numbers of controls with genotypes AA, Aa and aa, respectively, under the rare disease approximation and HWE. These estimates are of the same form as those obtained from the two-by-three contingency table that cross-classifies the genotype and case-control status should the genotype be available for deceased cases, except that the “observed” counts are replaced by the “estimated” (for cases) or “expected” (for controls) counts. These estimators are also very similar to those obtained by Chen and Chatterjee [12] for estimating OR association parameters with case-control data under the constraint of HWE in the control population, where they reported improved statistical efficiency when the observed numbers of controls were replaced by the “predicted” under HWE.

The expressions for β̂₁ and β̂₂ involve the estimated survival probabilities q̂₀, q̂₁ and q̂₂. But it turns out that two of the score functions for the three suvival probabilities are equivalent, resulting in only two independent score equations. One cannot uniquely solve for three independent parameters from only two equations without additional constraints. Therefore, these three parameters as well as the two association parameters are not identifiable when a co-dominant model is adopted for both association and survival. Intuitively, this is because the genotype information of children and/or spouse is not fully informative in predicting cases’ genotype. For example, when parents have genotype Aa and aa, one will expect that their child’s genotype is Aa with probability 0.5 and aa with probability 0.5. However, when one child has genotype aa and the spouse has genotype Aa, one will only know that the case parent has genotype Aa or aa but cannot estimate the probabilities without taking advantage of the risk parameters for disease or survival.

When either the association model (1) or the survival model adopts an additional constraint, the parameters become identifiable. We note that children and spouses’ genotype data are involved in formulas both for β and (q₀, q₁, q₂). Consequently, with genotype data from children and spouses, it is feasible to obtain maximum likelihood estimates that are consistent and at the same time assess the magnitude of survival bias. Below we provide estimates of OR parameters for association and survival probabilities under two commonly considered models. For each model, we consider three different scenarios of how family members of deceased cases are available: the general mixed scenario where genotype data for one child and spouse, or only for one child, or only for spouse is available for all or for a subset of deceased cases; one child and spouse scenario where genotype data for one child and spouse is available for some or all deceased cases; and one child only scenario where genotype data for only one child is available for all or some of the deceased cases. We also describe an extension of these results for studying gene-environment interactions. Here the estimates of log OR for association also resemble those if genotype data were available for cases, except that the genotype counts for cases and controls are replaced by the estimated (for cases) and the expected (for controls), respectively.

2.1 Modeling association as log-additive and survival as co-dominant

Under a log-additive association model for risk and a co-dominant model for survival, we obtained closed-form MLEs that incorporate family genotype data. The MLE for the log OR for association is

$${\widehat{\beta }}_1=log\frac{({\widehat{N}}_{11}+2{\widehat{N}}_{12}){\widehat{N}}_{01}}{2({\widehat{N}}_{11}+2{\widehat{N}}_{10}){\widehat{N}}_{02}},$$

where again N̂₀₀ = N₀(1−p̂_a)², N̂₀₁ = 2N₀p̂_a(1−p̂_a), ${\widehat{N}}_{02}=N_0{\widehat{p}}_a^2$, and N̂₁₀ + N̂₁₁ + N̂₁₂ are the inverse probability weighted counts, with N̂₁₀ = n₁₀/q̂₀, N̂₁₁ = n₁₁/q̂₁, and N̂₁₂ + n₁₂/q̂₂ (Web Appendix). The MLEs for the three survival probabilities take the following forms:

$${\widehat{q}}_0=\frac{n_{10}}{N_1{\left(1-{\widehat{p}}_a^{\ast }\right)}^2},{\widehat{q}}_1=\frac{n_{11}}{2N_1{\widehat{p}}_a^{\ast }\left(1-{\widehat{p}}_a^{\ast }\right)},\text{and}{\widehat{q}}_2=\frac{n_{12}}{N_1{\left({\widehat{p}}_a^{\ast }\right)}^2},$$

where ${\widehat{p}}_a^{\ast }$, the estimated allele prevalence among affected individuals, takes the form ${\widehat{p}}_a^{\ast }=\left(2M_a+n_{11}+2n_{12}\right)/2N_1$. For the three scenarios to be described below, M_a and the estimated MAF p̂_a will take different forms and be defined differently. Note that M_a is not a parameter but an intermediate expression to represent half the estimated total number of copies of a in the ungenotyped cases, i.e. the part in ${\widehat{p}}_a^{\ast }$ that differs among the three scenarios. Later in this section we will give an intuitive explanation for ${\widehat{p}}_a^{\ast }$ and M_a. The scenarios considered in sections 2.1.2 and 2.1.3 are special cases of that to be described in section 2.1.1.

2.1.1 The General Mixed Scenario

We first consider a design where a representative sample of deceased cases has either a spouse or child or both available for genotyping. Let m_O denote the number of deceased cases who do not have child genotype data available. Let m_1A (m_1a) be the number of deceased cases for whom we have a genotyped child and who must have passed allele A(a) to the child, m_1Aa be the number of deceased cases for whom we have a genotyped child and the child has genotype Aa, m_1* be the number of deceased cases whose family members’ genotypes provide no information in predicting cases’ genotype. These counts are calculated as m_1A = m₀₀ + m₀₁ + m₁₂ + m_0c + m₀₊ + m₁₂, m_1a = m₁₀ + m₂₁ + m₂₂ + m_2c = m₁₀ + m₂₊, m_1Aa + m_1c, and m_1* = m₁₁ + m_O. Then M_a mentioned above is the positive solution of the following quadratic equation, which is obtained directly by solving the likelihood score equation (See Web Appendix):

$$\frac{1-2p_a}{p_a}\left(m-m_{1\ast }\right)M_a^2+m\left[m-m_{1\ast }-m_{1Aa}-\frac{1-2p_a}{p_a}\left(m_{1a}+m_{1Aa}\right)\right]M_a-m^2{m}_{1a}=0.$$

There is no closed-form solution for the maximum likelihood estimator for the MAF p_a. Therefore we obtained the profile likelihood for p_a based on the closed forms of q̂₀, q̂₁, q̂₂ and β̂₁, and maximized it numerically. Because of the correlation between parental genotypes conditional on the child’s genotype, incorporating the spouse genotype data should increase the precision of estimating both the association parameter β₁ (through more precise estimation of p_a) and the survival probabilities. We note that the scenarios considered in Sections 2.1.2 and 2.1.3 are both special cases of this general scenario. When for every deceased case only one child is recruited, m_jk = 0 for all j and k. When for every deceased case both the spouse and one child are recruited, m_jc = 0 for all j.

2.1.2 The One Child and the Spouse Scenario

Under this scenario, we assume that genotype data for one child and the spouse are available for all or a representative sample of the deceased cases. We calculated M_a and derived the MAF estimate p̂_a as:

$$M_a=\frac{m{m}_{1a}}{m-m_{1\ast }}=\frac{m(m_{2+}+m_{10})}{m-m_{1\ast }},{\widehat{p}}_a=\frac{N_{01}+2N_{02}+m_{1p}+2m_{2p}}{2(N_0+m_{+p})}.$$

Here m_1a = m₁₀ + m₂₊ according to section 2.1.1, m_1p and m_2p are the numbers of deceased cases who have spouse genotype Aa and aa, respectively, and m_+p = m_0p + m_1p + m_2p. Note that the MAF estimate p̂_a uses data for both controls and spouses of the deceased cases. This is because the spouses do not have the disease and can be treated as an independent source of data for estimating the MAF.

The terms M_a and ${\widehat{p}}_a^{\ast }$ have intuitive interpretations. For the m₂₊ deceased cases whose child’s genotype is aa and m₁₀ cases whose child has genotype Aa and spouse has genotype AA, each case must have passed an “a” allele to the child. Similarly, for the m₀₊ deceased cases whose child’s genotype is AA and the m₁₂ cases whose child has genotype Aa and spouse has genotype aa, each case must have passed an “A” allele to the child. Thus there are m₂₊ + m₁₀ and m₀₊ + m₁₂ deceased cases who passed “a” and “A” to the offspring, respectively. Note that m−m_1* = m₂₊ + m₁₀ + m₀₊ + m₁₂. Since “A” and “a” have equal probability to be transmitted from a heterozygous parent to his/her child, the total number of deceased cases who have passed “a” alleles can be estimated as $m\frac{m_{2+}+m_{10}}{m-m_{1\ast }}$, which is M_a. The number of surviving cases who have passed “a” alleles to the offspring is estimated as $\frac{n_{11}}{2}+n_{12}$. Then the estimated total number of cases passing “a” alleles to their offspring is $M_a+\frac{n_{11}}{2}+n_{12}$. Define the estimated MAF among cases as ${\widehat{p}}_a^{\ast }=\widehat{p}(a\mid Y=1)$ then

$${\widehat{p}}_a^{\ast }=\frac{M_a+\frac{n_{11}}{2}+n_{12}}{N_1}=\frac{2M_a+n_{11}+2n_{12}}{2N_1}.$$

Note that ${\widehat{p}}_a^{\ast }$ is a consistent estimator for the MAF in the case population also because the genotype in the case population conforms to HWE under the log-additive risk model.

2.1.3 One Child only Scenario

We next consider a design where a representative sample of cases has a child available for genotyping and spouses are not genotyped. Sometimes it may be feasible to obtain genotype data only for offspring, but not spouses. Let m_0c, m_1c, m_2c be the respective number of children with genotype AA, Aa, aa, and m_O = m−m_+c the number of deceased cases without child genotype data. In this case, M_a is the positive solution of the following quadratic equation:

$$\frac{1-2p_a}{p_a}\left(m-m_O\right)M_a^2+m\left[m_{0c}+m_{2c}-\frac{1-2p_a}{p_a}\left(m_{2c}+m_{1c}\right)\right]M_a-m^2{m}_{2c}=0.$$

No closed form estimate exists for the MAF. Therefore we obtained the profile likelihood for p_a, which is a function of the closed-form estimates q̂₀, q̂₁, q̂₂, and β̂₁, and maximized it numerically as for the general scenario.

2.2 Use of dominant coding for both association and survival

We next consider the use of a dominant model for survival. This version may be needed in situations, e.g., if the frequency of the minor allele under study is low, where a co-dominant model for survival becomes impractical due to sparse data and more parsimonious models become necessary. With a dominant model for both association and survival, the MLEs are calculated using methods similar to those of section 2.1 as follows. For all the three scenarios considered in section 2.1, the estimated OR association parameter takes the form

$${\widehat{\beta }}_1=log\frac{\left({\widehat{N}}_{11}+{\widehat{N}}_{12}\right){\widehat{N}}_{00}}{\left({\widehat{N}}_{01}+{\widehat{N}}_{02}\right){\widehat{N}}_{10}},$$

where N̂₀₀, N̂₀₁, and N̂₀₂ are the predicted genotype counts in controls under HWE as described previously,

$${\widehat{N}}_{10}=N_1\left(1-{\widehat{p}}_a^{\ast \ast }\right),{\widehat{N}}_{11}=N_1{\widehat{p}}_a^{\ast \ast }\frac{n_{11}}{n_{11}+n_{12}},{\widehat{N}}_{12}=N_1{\widehat{p}}_a^{\ast \ast }\frac{n_{12}}{n_{11}+n_{12}}.$$

Here ${\widehat{p}}_a^{\ast \ast }=\frac{\left(2-{\widehat{p}}_a\right)M_a+n_{11}+n_{12}}{N_1}$, and M_a takes the same forms for the three scenarios as in section 2.1.1, 2.1.2 and 2.1.3, respectively. Note that M_a has the same interpretation as in section 2.1.2. Then (2−p̂_a)M_a can be interpreted as the estimated number of deceased cases who have at least one copy of the minor allele. Since n₁₁ + n₁₂ is number of surviving cases who carry the minor allele, ${\widehat{p}}_a^{\ast \ast }$ is the estimated proportion of cases who carry the minor allele. Under this dominant model, we obtained p̂_a based on its profile likelihood.

2.3 Extension of the Above Results for Assessing G-E interactions

The estimation and testing of multiplicative G-E interaction effects will also be subject to survival bias. Suppose that a binary exposure E influences the occurrence of disease and might also influence survival conditional on disease. We assume E is available for all N₀ +N₁ study participants, regardless of availability of genotype data. If survival is multiplicative in E effects and G effects, and if both survival and association depend on the same binary coding for G or the association model (but not the survival model) depends on co-dominant coding for G, then the naïve estimate of the multiplicative G-E interaction OR parameter from standard logistic regression analysis and the accompanying standard error estimate are valid according to theoretical results for two-phase studies [13]. Of course the naïve main-effect OR estimates for G and for E would typically be biased. On the other hand, if survival depending on G follows a co-dominant model and the occurrence of disease depends on G through a log-additive model, then naïve estimates of both the main and interaction effect OR parameters would often be biased. The methods in the first two subsections can be extended to obtain consistent estimates of all OR parameters. Consider a simple logistic regression model for disease occurrence that quantifies the joint effect of a di-allelic SNP and a binary environmental variable:

$$p(Y=1\mid G,E)=\frac{e^{{\beta }_0+{\beta }_{g}f(G)+{\beta }_{e}E+{\beta }_{I}f(G)\times E}}{1+e^{{\beta }_0+{\beta }_{g}f(G)+{\beta }_{e}E+{\beta }_{I}f(G)\times E}},$$

where f(G) is defined as in Equation (1), and E takes the value 1 or 0. Let N_ijk denote the total number of subjects with Y=i (i = 0, 1), G=j (j = 0, 1, 2), and E=k (k=0, 1). Let N̂_1jk be the “predicted number” of cases defined as above through inverse probability weighting. Under the assumptions of G/E independence and HWE in the source population, and initially assuming that survival depends only on G and not on E, we derived estimates of all association parameters. Note, however, that G/E independence is only assumed here for convenience of demonstrating our method and not needed for our general proposed design. If f(G) expresses log-additive coding and h(G) co-dominant coding, we obtain the same estimates as those in Section 2.1 for the population MAF p_a and the survival probabilities (q₀, q₁, q₂) and

$$e^{{\widehat{\beta }}_e}=\frac{{\widehat{N}}_{1+0}{N}_{0+0}{\left({\widehat{N}}_{111}+2{\widehat{N}}_{101}\right)}^2}{{\widehat{N}}_{1+1}{N}_{0+1}{\left({\widehat{N}}_{110}+2{\widehat{N}}_{100}\right)}^2},e^{{\widehat{\beta }}_g}=\frac{\left(1-{\widehat{p}}_a\right)\left({\widehat{N}}_{110}+2{\widehat{N}}_{120}\right)}{{\widehat{p}}_a\left({\widehat{N}}_{110}+2{\widehat{N}}_{100}\right)},e^{{\widehat{\beta }}_I}=\frac{\left({\widehat{N}}_{110}+2{\widehat{N}}_{100}\right)\left({\widehat{N}}_{111}+2{\widehat{N}}_{121}\right)}{\left({\widehat{N}}_{111}+2{\widehat{N}}_{101}\right)\left({\widehat{N}}_{110}+2{\widehat{N}}_{120}\right)}.$$

Under a dominant model for both f(G) and h(G), estimates of q̂₀, q̂₁, q̂₂ are the same as those in Section 2.2, and the estimates of the OR parameters are

$$e^{{\widehat{\beta }}_e}=\frac{N_{0+0}{\widehat{N}}_{101}}{N_{0+1}{\widehat{N}}_{100}},e^{{\widehat{\beta }}_g}=\frac{{(1-{\widehat{p}}_a)}^2({\widehat{N}}_{110}+{\widehat{N}}_{120})}{{\widehat{p}}_a(2-{\widehat{p}}_a){\widehat{N}}_{110}},\text{and}{e}^{{\widehat{\beta }}_I}=\frac{{\widehat{N}}_{100}({\widehat{N}}_{111}+{\widehat{N}}_{121})}{{\widehat{N}}_{101}({\widehat{N}}_{110}+{\widehat{N}}_{120})}.$$

The two interaction parameter estimates above only involve data for cases and their families and reduce to case-only estimates [14] under G/E independence in the absence of survival bias. The association parameter estimators resemble those derived in Chen et al. [15] in the absence of survival bias, except that the observed counts in cases are replaced by the estimated counts obtained through inverse-probability weighting. Similar results can be obtained when survival depends on E both through its main effect and interaction with h(G), where survival probabilities at each G/E combination need to be estimated.

3. Simulations

We performed numerical studies to evaluate the performance of the proposed methods in realistic scenarios for assessing marginal effects of G. Imposing our rare phenotype assumption, we generated SNP genotypes for controls under HWE, and for cases from the derived distribution

$$p\left(G\mid Y=1\right)=\frac{e^{\beta f(G)}p\left(G\mid Y=0\right)}{{\displaystyle \sum _{g=0,1,2}}{e}^{\beta f(g)}p\left(G=g\mid Y=0\right)},$$

where the coding we impose is either log-additive, f(G)= the number of copies of the minor allele, or dominant, f(G)=I(number of copies of the minor allele > 0). We generated the indicator for failure to survive, S=0, from the mixture distribution

$$p(S=0\mid G,Y=1)=\rho +(1-\rho )\frac{e^{h(G)}}{1+e^{h(G)}},0<\rho <1.$$

Note that we do not fit this mixture distribution directly but make use here of the fact that without knowing the true missing mechanism, we are still able to obtain unbiased estimates of the survival probabilities and disease odds ratios as long as probabilities of survival are allowed to be different for people with different genotypes. We used a log-additive h (G) = α₀ + α₁G when generating S but fitted the less restrictive co-dominant model for h(G) when the association model was log-additive, and used dominant coding for both fitting and generating S when the true association model was dominant. We refer to e^α₁ as the “OR for death” below. Thus the true p(S=0 | G,Y =1) depends on G in a co-dominant or dominant fashion. Cases with S = 0 were treated as “deceased” in the analysis. We used random survival as the gold standard for comparison, which was generated by setting α₁ = 0. Then we generated two separate indicator variables R_c and R_p for the general mixed scenario from the models p (R_c = 1| S = 0,G,Y = 1) = γ_c and p (R_p = 1| S=0,G,Y=1) = γ_p, where R_c = 1 and R_p = 1 indicated that the genotype data was available for the child and spouse. Similarly, for scenarios where the child/spouse scenario genotype data for the child and spouse are available or not, as a pair, we generated only one indicator R from p (R = 1| S = 0,G,Y = 1) =γ. For the child-only scenario, we generated indicator R_c from p (R_c = 1| S = 0,G,Y = 1) = γ_c. Below we refer to γ_c, γ_p, and γ as “recruiting probabilities”. We used a MAF of 0.2 and for α₀ a value of −2.0, and each selected scenario was simulated 5,000 times.

Table 1 presents results showing the magnitude of survival bias for an analysis that simply excludes data for deceased cases, based on 5000 simulations. When the tested variant was independent of or only modestly associated with death (e^α₁ < 1.4), the bias in estimation was small, and the type I error rates were close to the nominal 0.05 level. When the variant was more strongly associated with death, the type I error rate became notably inflated. When only 30% of the missing genotype data were missing due to reasons not related to G and 70% were missing due to G-related causes, under the log-additive model for association and co-dominant model for survival, with the OR for death being 2.0, the missing genotype data rates corresponding to the three genotypes AA, Aa, and aa were 0.38, 0.45, and 0.55 respectively. The observed type I error rate corresponding to a nominal 0.05 was 0.145 when deceased cases were naively ignored in standard likelihood ratio tests of association. Our method maintained nominal type-I error rates in all scenarios. In general, the bias in the naïve estimation of the association OR parameter was small. For example, the mean estimate was 1.58 when the true value for association was 1.8 and the OR for death (e^α₁) was 2.0 (data not shown). Similar observations were made when a dominant model was adopted for both survival and association (with the data simulation and the analytic models corresponding). Table 2 presents the average log OR estimates and the estimated standard deviations. The average estimates obtained by our method were close to the true value. As expected, the child and spouse scenario resulted in the lowest standard deviations, while the child-only scenario had the highest standard deviations. The estimates without accounting for survival (rows “Naïve”) appeared to be biased, but the bias was small.

Table 1.

Estimated OR and Type I Error Rates for Testing Association (nominal level = 0.05) by FSD or when Deceased Cases were Naively Ignored.

Association Model	Survival Model	Method	True OR for Death (eα1)
			1.0	1.2	1.4	1.8	2.0
Log-additive	Co-dominant	Naïve	1.00 | 0.048	0.97 | 0.049	0.95 | 0.059	0.90 | 0.101	0.88 | 0.145
			1.00 | 0.049	0.97 | 0.051	0.95 | 0.058	0.90 | 0.084	0.88 | 0.110
		FSD	1.00 | 0.047	1.00 | 0.047	1.00 | 0.048	1.00 | 0.045	1.00 | 0.044
			1.00 | 0.048	1.00 | 0.048	1.00 | 0.047	1.00 | 0.049	1.00 | 0.048
Dominant	Dominant	Naïve	1.00 | 0.051	0.98 | 0.050	0.96 | 0.054	0.91 | 0.087	0.89 | 0.110
			1.00 | 0.049	0.98 | 0.053	0.95 | 0.057	0.91 | 0.073	0.89 | 0.087
		FSD	1.00 | 0.046	1.00 | 0.046	1.00 | 0.047	1.00 | 0.046	1.00 | 0.049
			1.00 | 0.045	1.00 | 0.046	1.00 | 0.047	1.00 | 0.047	1.00 | 0.048

^*The first row corresponds to mixture proportion ρ=0.3, and the second corresponds to ρ=0.6. Before “|” is the estimate of e^β₁ and after is the type-I error rate for a nominally 0.05-level test of the incidence association parameter.

Table 2.

Parameter Estimation under Different Models and Scenarios for Genotyping Family Members of Deceased Cases.

Model	Odds Ratioa	γb	Estimates (S.D.)
			Mixed	Child + Spouse	Child Only
Log-additive for association and co-dominant for survival	log(1) = 0	1	−0.002 (0.120)	−0.004 (0.120)	−0.005 (0.162)
		0.7	−0.002 (0.140)	−0.004 (0.132)	−0.002 (0.175)
		0.5	−0.004 (0.163)	−0.002 (0.146)	−0.009 (0.192)
		0(Naive)		−0.051 (0.130)
	log(1.4) = 0.336	1	0.336 (0.113)	0.334 (0.113)	0.340 (0.147)
		0.7	0.335 (0.131)	0.339 (0.124)	0.335 (0.158)
		0.5	0.333 (0.151)	0.336 (0.136)	0.337 (0.172)
		0(Naive)		0.286 (0.123)
	log(1.8) = 0.588	1	0.588 (0.109)	0.589 (0.109)	0.589 (0.139)
		0.7	0.583 (0.126)	0.588 (0.119)	0.587 (0.149)
		0.5	0.585 (0.144)	0.585 (0.131)	0.583 (0.162)
		0(Naive)		0.539 (0.120)
Dominant for both association and survival	log(1) = 0	1	0.000 (0.143)	0.001 (0.143)	0.001 (0.193)
		0.7	0.004 (0.169)	−0.004 (0.159)	0.002 (0.210)
		0.5	−0.002 (0.197)	−0.003 (0.176)	−0.001 (0.231)
		0(Naive)		−0.046 (0.148)
	log(1.4) = 0.336	1	0.340 (0.143)	0.337 (0.143)	0.336 (0.188)
		0.7	0.336 (0.168)	0.336 (0.158)	0.337 (0.204)
		0.5	0.338 (0.195)	0.337 (0.176)	0.338 (0.224)
		0(Naive)		0.291 (0.144)
	log(1.8) = 0.588	1	0.590 (0.145)	0.590 (0.145)	0.591 (0.187)
		0.7	0.589 (0.170)	0.592 (0.161)	0.589 (0.204)
		0.5	0.592 (0.197)	0.594 (0.179)	0.586 (0.224)
		0(Naive)		0.546 (0.143)

^aThe odds ratio of association.

^bRecruiting probability for family members.

^*Sample size is 500 for cases and 500 for controls; ρ = 0.3, α₀ = −2, and e^α₁ = 1.4 (with survival probabilities 0.62, 0.59 and 0.55 for each genotype.

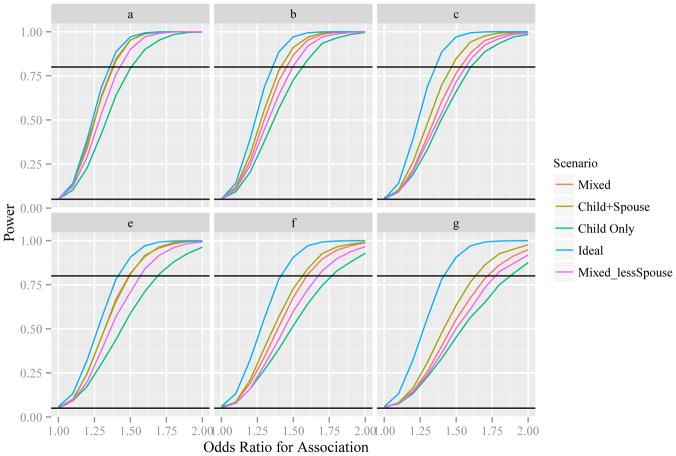
Figure 1 displays the powers under different models, scenarios and recruiting probabilities. In both the general mixed (“Mixed”) and child and spouse (“Child+Spouse”) scenarios, the recruiting probabilities for children and spouses were assumed to be 1, 0.7 or 0.5. In the child-only (“Child”) scenario, children had recruiting probabilities 1, 0.7 or 0.5. Except for the three scenarios in sections 2.1, we considered two additional scenarios: the ideal one where all cases survived, and the general mixed scenario where the recruiting probability of spouses was half of that of children (“Mixed_less Spouse”). That is, when the recruiting probabilities γ_c for children were assumed to be 1, 0.7 or 0.5, the corresponding recruiting probabilities for spouses γ_p were 0.5, 0.35, and 0.25, respectively. The power appeared to be in increasing order from Child-Only, Mixed_less Spouse, Mixed, Child + Spouse to Ideal. When the recruiting probability was 1 in the log-additive model, the powers of both the Mixed and Child + Spouse scenarios were close to the ideal. Not surprisingly, the power of all scenarios decreased with decreasing recruiting probabilities. For example, under the model of log-additive coding for association (odds ratio 1.4) and co-dominant coding for survival, in the Mixed scenario, the powers corresponding to recruiting probabilities 1, 0.7 and 0.5 were 0.848, 0.723 and 0.606, respectively.

Figure 1.

Power plot.

a. Log-additive model for association and co-dominant model for survival, recruiting probability = 1. In this case, Mixed and the Child+Spouse designs are identical, and the minor difference in the figure was due to computation precision;

b. Log-additive model for association and co-dominant model for survival, recruiting probability = 0.7;

c. Log-additive model for association and co-dominant model for survival, recruiting probability = 0.5;

d. Dominant model for both association and survival, recruiting probability = 1; In this case, Mixed and the Child+Spouse designs are identical, and the minor difference in the figure was due to computation precision;

e. Dominant model for both association and survival, recruiting probability = 0.7;

f. Dominant model for both association and survival, recruiting probability = 0.5.

Interestingly, although the spouse genotype itself provides no information in predicting the case’s genotype, inclusion of spouses together with the child genotype can improve the power noticeably. Consider testing the association of a SNP under the log-additive coding with OR 1.4. Consider that genotype data is available for 500 controls and that the survival probabilities are 0.62, 0.59 and 0.55 for cases with genotype AA, Aa, and aa respectively. Assume that genotype data are also available for family members of 70% of deceased cases. If 70% of children of the deceased cases provided genotype information, the power was 0.565. If 70% of spouses of the deceased cases were also randomly available, then on average, about half (49%) of the deceased cases have both children and spouses genotype. The study power under this setting was 0.723. If genotype data were jointly available for the child and spouse as a pair for 70% of the deceased cases, the study power increased to 0.782. A natural question that arises under a fixed budget is: which one, recruiting x children or x/2 Child + Spouse pairs, would yield higher study power? As stated previously, the power was 0.565 with genotype data for 70% children. The power increased to 0.595 with genotype data for 35% child and spouse pairs. Similarly, compared to the power 0.640 when genotyping only children of all the deceased cases, genotyping both the child and the spouse of half of the deceased cases yielded higher power, 0.682.

Even when survival was independent of G but the possible dependence of survival on G was nevertheless modeled, our design achieved an increase in power by incorporating family genotype data and exploiting the HWE assumption, partly through the improved estimation of the MAF. With β₁ = ln(1.2) and β₁ = ln(1.4) (data not shown), the power by the likelihood ratio test based on standard logistic regression with surviving cases only was 0.322 and 0.792, respectively, which are lower than those with the proposed method, 0.356 and 0.853. When both models were dominant, the corresponding powers were 0.247 and 0.658 versus 0.257 and 0.676, respectively.

4. Application to a Study of Breast Cancer Genetics

We analyzed a dataset that was derived from the Two Sister Study (http://sisterstudy.niehs.nih.gov/English/studies.htm). Although the study design was based on young-onset breast cancer in the daughters, the analysis presented here is based on the occurrence of breast cancer in the mothers. The dataset included 291 women who had in the past been diagnosed with breast cancer and 645 female controls who had never been diagnosed with breast cancer. Genetic information on 6 SNPs from the gene FGFR2 (rs3750817, exm.rs2981579, rs2981578, exm.rs2981575, rs1219648, rs2981582) were available for all 645 controls but for only 126 cases. The additional 165 cases who could not be genotyped had a daughter (or daughters) or spouse who had been genotyped as part of the study. Therefore, for those 165 mothers we used the daughters’ genotype data to supplement their missing mother’s genotype, using one from each family (preferring an unaffected daughter if two were available). Among the 165 missing cases, 29 had both a daughter and the daughter’s father available for genotyping and 135 had only a daughter available. The remaining missing case had no family members available and was omitted from analysis. For each SNP, we conducted two analyses, each applying log-additive coding for risk: (1) we fit a logistic regression model, simply omitting the ungenotyped cases (column “Naïve”); and (2) we applied the proposed FSD (assuming co-dominant coding for missingness) to the dataset where we made use of the proxy family members for cases with missing genotypes, enabling inclusion of 290 cases instead of 126 cases (column “FSD”). Note that although the mechanism for missing genotype was, for simplicity, assumed to be death in the description of the methods given above, we here think of it more broadly as genotype-related missingness.

A test of Hardy-Weinberg equilibrium based on controls yielded reassuringly hefty p values for all 6 of the SNPs (data not shown), verifying an assumption needed for FSD. Results based on the three analytic methods applied for assessing effects of FGFR2 on risk of breast cancer are shown in Table 3. We calculated the estimates for the OR parameters and log OR parameters with standard errors for each SNP with both methods, and calculated tail probabilities for the Z statistics as the log OR divided by the standard error (column “P-value”). In Table 4, we provide the “survival” probabilities (more accurately, recruitability) for each of the three genotypes for each SNP.

Table 3.

OR Estimates By the Naïve and FSD methods for SNPs.

SNPs	OR Estimates			Log OR Estimates (S.E.)			P-Value
	Naïve	FSD	FSDf	Naïve	FSD	FSDf	Naïve	FSD	FSDf
rs3750817	0.809	0.753	0.830	−0.213 (0.142)	−0.283 (0.153)	−0.186 (0.127)	0.1333	0.0640	0.1432
exm.rs2981579	1.341	1.518	1.323	0.294 (0.138)	0.418 (0.159)	0.280 (0.126)	0.0329	0.0085	0.0263
rs2981578	0.689	0.628	0.702	−0.373 (0.139)	−0.465 (0.161)	−0.354 (0.127)	0.0072	0.0038	0.0052
exm.rs2981575	1.382	1.457	1.379	0.324 (0.136)	0.377 (0.155)	0.321 (0.126)	0.0175	0.0154	0.0108
rs1219648	1.376	1.477	1.367	0.319 (0.137)	0.390 (0.156)	0.313 (0.126)	0.0195	0.0123	0.0133
rs2981582	1.349	1.577	1.338	0.299 (0.136)	0.456 (0.155)	0.291 (0.126)	0.0281	0.0032	0.0204

^*The Naïve method utilizes the observed data only and ignores the ungenotyped cases. The FSD method assumes that cases with different genotypes (AA, Aa and aa) have different “survival” probabilities (q₀, q₁ and q₂) and incorporates genotype information of family members of ungenotyped cases. The FSD^f method is the same as FSD except for assuming equal survival probabilities (q₀ = q₁ = q₂ = q).

Table 4.

Recruitability (“Survival”) Probabilities Estimated By FSD for SNPs.

SNPs	FSD			FSDf
	AA	Aa	aa
rs3750817	0.417 (0.053)	0.425 (0.052)	0.527 (0.130)	0.433 (0.044)
exm.rs2981579	0.465 (0.088)	0.462 (0.050)	0.356 (0.067)	0.433 (0.059)
rs2981578	0.392 (0.061)	0.451 (0.051)	0.472 (0.106)	0.433 (0.050)
exm.rs2981575	0.437 (0.080)	0.454 (0.049)	0.389 (0.073)	0.433 (0.058)
rs1219648	0.432 (0.079)	0.467 (0.050)	0.366 (0.071)	0.433 (0.058)
rs2981582	0.462 (0.083)	0.474 (0.050)	0.328 (0.066)	0.433 (0.057)

^*The Naïve method utilizes the observed data only and ignores the ungenotyped cases. The FSD method assumes that cases with different genotypes (AA, Aa and aa) have different “survival” probabilities (q₀, q₁ and q₂) and incorporates genotype information of family members of ungenotyped cases. The FSD^f method is the same as FSD except for assuming equal survival probabilities (q₀ = q₁ = q₂ = q).

Although the standard errors of the Naive method are slightly smaller than those from FSD, with this example the FSD method always results in more significant P-values. For example, for the first SNP rs3750817, the Naive method indicated no association between breast cancer and this SNP, while the FSD method obtained a marginally significant P-value. Similarly, for the last SNP rs2981582, the P-value from FSD (0.003) is much smaller than that from the Naive method (0.028), where the latter is not significant after the Bonferroni adjustment of testing 6 SNPs.

The FSD method also enables us to explore whether missingness is related to genotype. Results are shown in Table 4, where “a” denotes the minor allele (the allele with prevalence less than 0.5). All of the p values for testing equality of the recruitability probabilities were above 0.24. Therefore, missingness did not seem to depend on the genotype for these FGFR2 SNPs. We then conducted a stage 2 analysis where we constrained q₀ = q₁ = q₂. Results are shown in Table 3, columns “FSD^f”. Here we have sacrificed protection against survival bias, but retained our ability to capture the supplemental information derived from proxy family members. Note that, relieved of its need to estimate those three parameters, the analysis now returned smaller standard errors than were achieved by the original naïve analysis that was shown in Table 3. It is interesting to observe the estimates by “Naïve” and “FSD^f” always yielded similar estimates, which may differ noticeably from that by FSD. This difference was due to the differential “survival” probabilities for women carrying different genotypes for each SNP, as shown in the “Survival Probabilities” column in Table 4. Therefore, we prefer to interpret association findings based on FSD, instead of “FSD^f”.

5. Discussion

The proposed design provides a useful approach for assessing and correcting survival bias in population-based case-control genetic association studies and improving power by enrolling offspring and spouses of deceased cases and making proxy use of their genotypes. The approach performed well for assessing both marginal genetic effects and gene-environment (G-E) interactions (unreported simulation results). It also yielded unbiased estimates of association parameters for survival (data not shown). In addition to HWE, we make the usual assumptions that cases and controls are drawn from the same source population and that the disease is rare. The current exposition considers a single di-allelic SNP in relation to association and survival and the same study design can be extended to study multiple genetic and environmental factors, through application of the EM algorithm. Our approach introduces a useful solution to a thorny non-ignorable missingness problem. Because it is based on a retrospective likelihood, mis-specification of the nuisance survival model may lead to biased estimates and inflated type-I error rate (Web Appendix Table 2). Therefore, a co-dominant model, which is always a correct model, should be fitted for survival whenever the data allows. We fit the log-additive or dominant model for survival only when the data is too sparse, i.e, the number of subjects for a genotype category is too small to fit a co-dominant model.

The family-supplemented design does have limitations. Because of identifiability issues one cannot use co-dominant models for both association and survival. The identifiability issue can presumably be resolved if genotype data could be made available for a random subset of deceased cases (not likely in practice), but the issue cannot be addressed by genotyping family members or obtaining richer marker genotype data. It is desirable to consider other design options to address this challenge. In addition, extending our proposed method to incorporate the survival time of the deceased cases may also prove helpful.

As is true generally for case-control genetic analyses, our method requires that there be no population stratification. We also implicitly assume there is no assortative mating related to the SNP under study and that the SNP is not related to fertility (i.e. the availability of a child to serve as a genetic proxy). However, we expect that a more robust approach can be devised for settings where there may be population stratification, using genetic control for population stratification, if we can approximate that the population that cases and controls are sampled from contains a finite number of discrete strata (e.g., [17]), mating is restricted to within-strata unions, and HWE holds within each stratum. Ancestry informative markers would need to be obtained for controls, live cases, and family members of deceased cases. Joint inference would be needed for association parameters, survival probabilities, stratum membership, and minor allele frequency (MAF) within each stratum. This task, at least computationally, is nontrivial and worth investigating in future research. Our proposed design can potentially be generalized to address survival bias in family-based case-control studies, which are largely free of bias from population stratification.

We focused the theory of our method on the scenario where genotype data can be obtained for one child and/or the spouse for each deceased case in a representative subsample. But in many realistic settings some deceased cases may not have a child available for genotyping but might have one or both parents available, while still others might provide a sibling, a child, or maybe a child and one parent. Under HWE and standard Mendelian transmission, the Expectation-Maximization (EM) algorithm [16] can be used to handle missing case genotypes under diverse family structures. In particular, the method is readily extensible to include multiple children with or without the spouse. If the number of family members recruited for each deceased case is specified a priori, then a relevant question is which family members are the most informative if they are equally recruitable. Clearly the spouse alone would not be very informative, whereas a single offspring alone would provide somewhat limited but informative genotype data as shown in the table and in the numerical studies. Other choices are not so clear. Consider two children versus one child and the spouse. When the two children have genotypes AA and aa, one can infer that the genotype for both parents is Aa. But other combinations of the genotypes may not be as informative as the same combination for one child and spouse (for example, if the two children have the same genotype). In some circumstances a priori knowledge of the biology might be needed. For example, if the gene under study may be related to longevity, the availability of the spouse may itself be selective (genotype-dependent), and children or siblings might be preferred for that reason. Nevertheless, we explored the most plausible scenarios in our theoretical and numerical studies, as recruitment of multiple children for a case may be practically challenging even if it were more efficient.

For conditions with young age at onset, such as birth defects, children and spouses will not be available at all and one would need to use the parents or siblings of cases as genetic informants. The genotypes of deceased (or therapeutically aborted) cases then become missing data and amenable to likelihood methods for estimation and testing through the EM algorithm.

We have focused on genotype data for a single SNP at a time. But genotype data at nearby markers could be helpful for infering the unobserved genotype data at that SNP and could usefully be incorporated into the likelihood analysis [18]. Consider another SNP with alleles B and b that is so close to our SNP of interest (which has alleles A and a) that the probability of recombination from parent to child (i.e. in a single meiosis) can be taken to be 0. Suppose the case had a child with genotypes Aa/Bb and spouse Aa/BB at the two loci. The child must carry either haplotypes AB and ab or haplotypes Ab and aB, while the spouse carries haplotypes AB and aB. The child must have inherited either AB or aB from the spouse. If Ab does not exist in the population, the case must have a copy of haplotype ab. Without genotype data for the second locus, the child and spouse genotype at the first locus, Aa/Aa, are less informative for the missing parent case’s genotype. Presumably, again the EM algorithm could be used to take advantage in this way of the LD structure in the genome for imputing missing genotypes, though the details are beyond our present scope.

In conclusion, when studying the role of genetics in causing a disease that can be fatal, survival bias can result in nonignorable missingness of genotype information. Under plausible assumptions, the genotyping of family members of deceased cases can both correct that bias and improve power for detecting genetic associations. Our methods are simple to implement and therefore can be applied to analyze genomewide association studies. Software for implementing this method is available from the authors upon request.

Supplementary Material

Appendix Figure 1. Appendix Figure 1.

Notational Diagram.

6. Appendix

Appendix Table 1.

Notational glossary.

N1	Number of cases, some living some deceased
N̂1j	Estimated number of cases with genotype j
N0	Number of controls, all genotyped
N̂0j	Estimated number of controls with genotype j
n1	Number of surviving cases
m	number of deceased cases (=N1−n1)
nij	Number with case status i and genotype j
mjk	Number of deceased cases with offspring genotype j and spouse genotype k
mjc	Number of deceased cases with offspring genotype j and no spouse genotype
mjp	Number of deceased cases with spouse genotype j
mO	Number of deceased cases with no offspring genotype information
m1A, m1a	Number of deceased case for whom we have a genotyped child and who must have passed allele A (a) to the child m1A = m00 + m01 + m12 + m0c = m0+ + m12; m1a = m10 + m21 + m22 + m2c = m10 + m2+
m1Aa	Number of deceased cases for whom we have a genotyped child and the child has genotype Aa; m1Aa = m1c
m1*	Number of deceased cases whose family members’ genotypes provide no information in predicting cases’ genotype; m1* = m11 + mO
Nijk	Number of subjects with case status i, genotype j, and environmental exposure k
Y	Disease status flag (1 if case)
G	Genotype of study participant
Gf, Gc, Gp	Genotype of deceased case’s family member(s)
Gc	Genotype of deceased case’s offspring
Gp	Genotype of deceased case’s spouse (the other parent of that offspring)
S	Survival status flag (1 if alive)
R, Rc, Rp	Flag for recruitability of family members, offspring and spouse for deceased case (1 if recruitable)
f(G)	Function of G for logistic association with disease
h(G)	Function of G for logistic association with death, given disease
β	Genetic association parameter for disease association model
ρ	Proportion of deceased cases whose death is unrelated to G
α	Genetic association parameter for death model that conditions on disease
pa	MAF in the control population
${\widehat{p}}_a^{\ast }$	Consistent estimator for the MAF in the case population
${\widehat{p}}_a^{\ast \ast }$	Consistent estimator for the proportion of subjects with a allele in the case population
γ	Proportion of family members who are not recruitable.