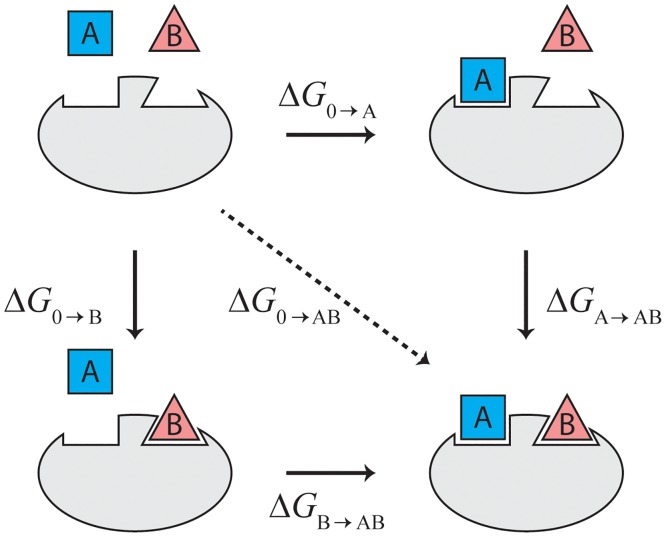
Fig 1. Bidirectional symmetry in allosteric systems.

Suppose that a protein can bind two different ligands, A and B, each at their respective sites. The difference in free energy ΔG_0→AB between a state with both ligands bound and one with neither ligand bound is independent of the order in which the ligands bind, so we can write it both as ΔG_0→AB = ΔG_0→B + ΔG_B→AB and as ΔG_0→AB = ΔG_0→A + ΔG_A→AB, implying that ΔG_0→B + ΔG_B→AB = ΔG_0→A + ΔG_A→AB. Rearranging this equation yields ΔG_A→AB − ΔG_0→B = ΔG_B→AB − ΔG_0→A. That is, the difference in the binding energy of ligand A with or without ligand B bound is the same as the difference in the binding energy of ligand B with or without ligand A bound. If one side of this equation is negative, the other must also be negative, and if one side is positive, the other must also be positive. Thus, if binding of ligand B is more favorable in the presence of A, then binding of ligand A is more favorable in the presence of ligand B (positive cooperativity). Likewise, if the presence of ligand A disfavors the binding of ligand B, then the presence of ligand B disfavors the binding of ligand A (negative cooperativity).