Fig. 11.

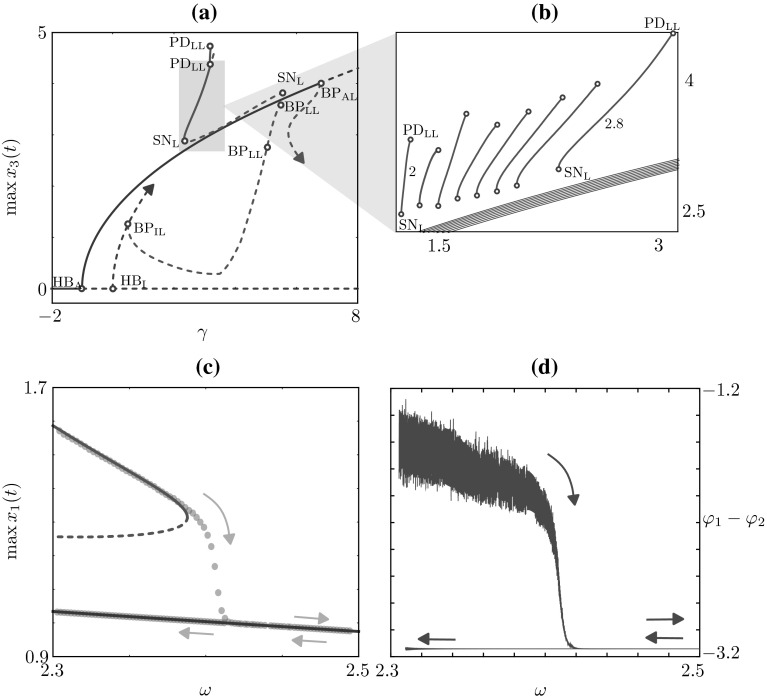
Bistability and hysteresis between anti-phase and phase-locked solutions. a The in-phase branch (blue) undergoes a symmetry-breaking bifurcation (${\text{BP}}_{\text{IL}}$) and the resulting unstable phase-locked branch, featuring two further symmetry-breaking bifurcations (${\text{BP}}_{\text{IL}}$), restabilises at a saddle-node bifurcation, before a period-doubling cascade takes place. A stable portion of the phase-locked branch (solid green line between ${\text{SN}}_{\text{L}}$ and ${\text{PD}}_{\text{LL}}$) coexists with the anti-phase branch originating at ${\text{HB}}_{\text{I}}$ (solid red branch). Parameters: $a=0.5$, $b=0.5$, $\mathit{\omega }=3$, $\mathit{\alpha }=-1.7$, $\mathit{\beta }=0.5$. b We repeat the experiment for $\mathit{\omega }\in [2,2.8]$ and plot stable branches to highlight the bistability region. c $\mathit{\omega }$ is varied by continuation and by quasi-static sweeps in direct numerical simulations (blue dots), for $\mathit{\gamma }=1.7$; the time simulation follows the phase-locked branch up to the saddle node at $\mathit{\omega }\approx 2.4$, where an abrupt and hysteretic transition to an anti-phase solution is observed. d Phase lag during numerical simulation in c (colour figure online)