Fig. 5.

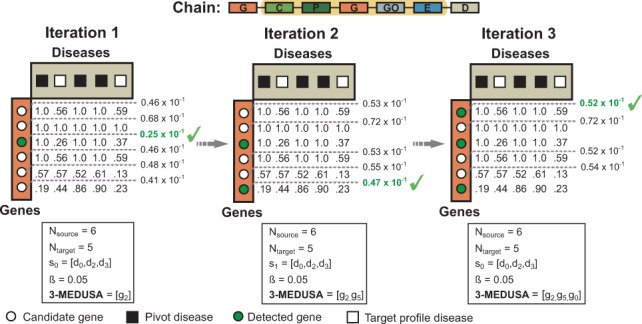
Inferring a three-maximally significant distant module with Medusa in the CPI regime. Shown is an example of a chain that relates six genes to five diseases via chemicals, pathways, genes, GO terms and exposure data (see the highlighted chain in Fig. 3). In this toy example, we are given three pivot diseases shown in black squares and would like to find a three-maximally significant gene module. Notice that we operate in the CPI data regime because the pivots (i.e. diseases) are of different type than the candidates (i.e. genes). In the first iteration, gene g₂ shows the most significant visibility for the pivot diseases (i.e. $p_{\text{CPI}}=0.25\times {10}^{-1}$) and is thus included into the module. Gene g₁ does not discriminate between the pivot and non-pivot diseases and is hence considered an unlikely candidate (i.e. $p_{\text{CPI}}=0.68\times {10}^{-1}$ in the first iteration and $p_{\text{CPI}}=0.72\times {10}^{-1}$ in later iterations). In second iteration, the algorithm picks g₅, although one might expect that g₁ would be selected due to its distinctive connections to the pivot disease. This is because Medusa detects modules that are not only highly visible to the pivot objects but are also diverse, which is important when trying to identify non-redundant comprehensive modules. Such behavior of Medusa is regulated by parameter β, which promotes diverse modules in this example, $\beta =0.05$. The final module is $M_3=\{g_2,g_5,g_0\}$