Fig. 1.

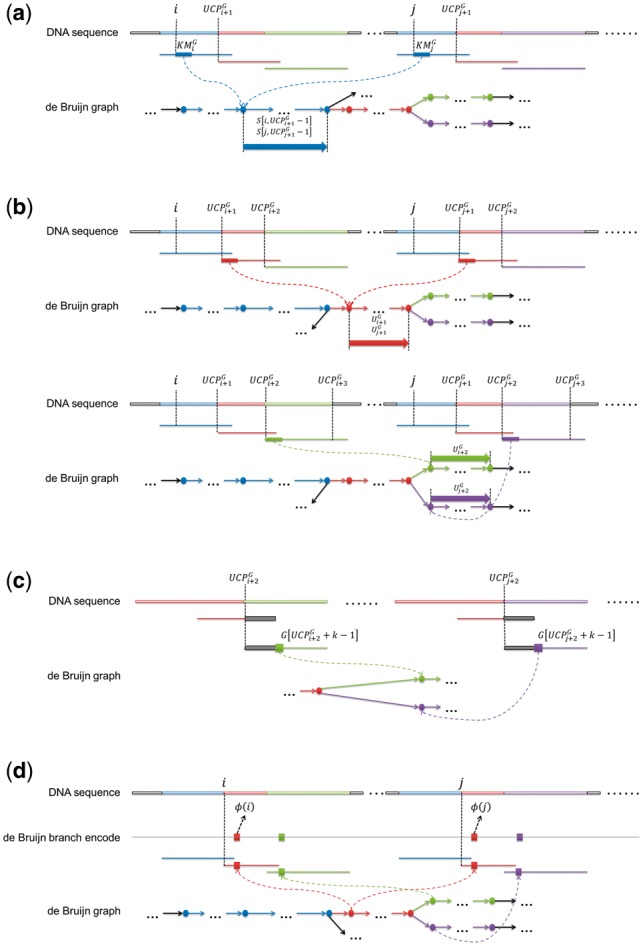
The unipath-based comparison between two suffixes with the same initial k-mer. (a) Because all the copies of the same k-mers collapse to the same vertex of the dBG, two suffixes, ${Suf}_i^G$ and ${Suf}_j^G$ with the same initial k-mer must link to the same offset of the same unipath (the copies of the unipaths on the DNA sequence are marked by segments with various colors). Thus, the lexicographical order of the two suffixes cannot be determined until the comparison reaches the end of the unipath, as all the corresponding characters of the two suffixes are same to each other. (b) When the comparison goes to new unipaths from the finished (same) unipath, the lexicographical order can be determined only if the two suffixes have two different unipaths on the corresponding positions of their unipath representation, otherwise, more unipaths are needed. In this case, both of the two suffixes have the same unipath (the red unipath) successive to the first unipath (the blue unipath), so that the comparison continues to the third unipaths. For the third unipath, the lexicographical order can be determined as the two suffixes goes to two difference branches (green and purple, respectively) at the end of the second unipath. (c) Owing to the property of dBG, two different unipaths must be different to each other at their first k-mers. Furthermore, if two different k-mers have the same precursor, their first (k-1) characters must be same to the last (k-1) characters of their precursor (the gray segments in the figure), i.e. the two branching k-mers are only different at their k-th character (the blocks marked as green and purple in the figure). In this situation, it only needs to compare the k-th characters of two unipaths to determine if they are the same unipath. (d) With this property, the de Bruijn encoding, ${\mathrm{d}\mathrm{E}}^G$, is defined as a string concatenating all such characters, $G\left[x+k\right],x=0,\dots ,\left|G\right|-k-1$, along the DNA sequence, $G$, where the k-mer, ${KM}_x^G$, at the position $x$ of $G$ is a copy of a multiple-out vertex. Each of the $G\left[x+k\right]$s is also termed as a branching character (marked as colored blocks in the figure). And for a position $j$ of $G$, $\varphi \left(j\right)$ is defined as the position of $Br\left(j\right)$ on ${\mathrm{d}\mathrm{E}}^G$, where $Br\left(j\right)$ is the branching character downstream and closest to the position j in $S$.