Fig. 2.
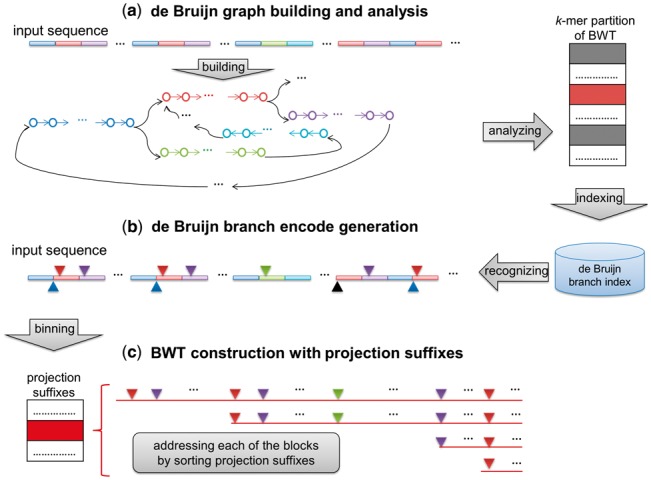
A schematic illustration of the deBWT method. (a) DeBWT initially builds a dBG of the input sequence(s) with a user-defined parameter, k, which determines the size of the vertices. The dBG is then analyzed to build the k-mer partition of the BWT and recognize all the unipaths (the colored bars in the figure indicate the copies of various unipaths of the input sequence). With the unipaths, all the multiple-in and multiple-out vertices are indexed by a hash table-based data structure, de Bruijn branch index. Moreover, all the multiple-in vertices are marked. In this case, the red block indicates the first k-mer of the ‘red’ unipath of the dBG which is a multiple-in vertex, and the grey and the white blocks respectively indicate other multiple-in and -out k-mers. (b) DeBWT scans the input sequence(s) to recognize the branching characters with de Bruijn branch index (marked as colored reverse rectangles above the input sequence) and generate the de Bruijn branch encoding. Meanwhile, the suffixes with initial k-mers corresponding to multiple-in vertices, i.e. the suffixes belonging to the unsolved parts of the BWT, are also recognized with the index (marked as colored rectangles below the input sequence). Furthermore, for each of the suffixes within the unsolved parts, deBWT calculates its value to determine the corresponding projection suffix and also recorded it into the de Bruijn branch index. (c) With de Bruijn branch index, deBWT addresses all the unsolved BWT parts by sorting the projection suffixes
