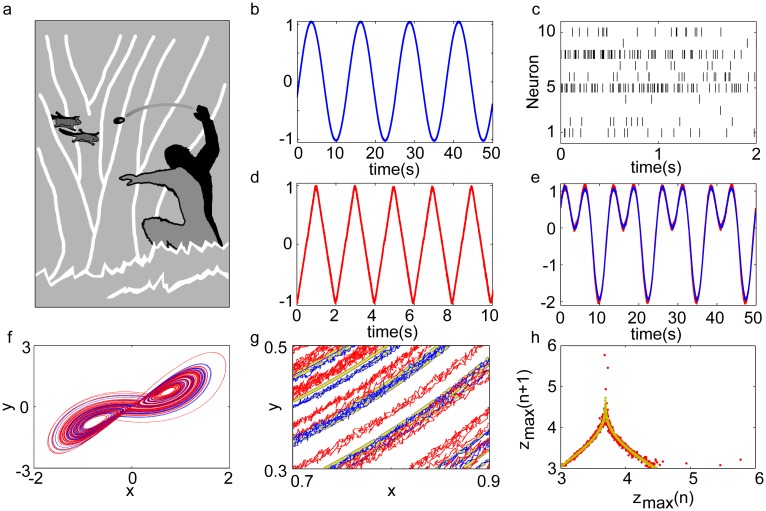
Fig 3. Learning dynamics with spiking neural networks.

(a): Schematic hunting scene, illustrating the need for complicated dynamical systems learning and control. The hominid has to predict the motion of its prey, and to predict and control the movements of its body and the projectile. (b-h): Learning of self-sustained dynamical patterns by spiking neural networks. (b): A sine wave generated by summed, synaptically and dendritically filtered output spike trains of a PCSN with nonlinear dendrites. (c): A sample of the network’s spike trains generating the sine in (b). (d): A saw tooth pattern generated by a PCSN with saturating synapses. (e): A more complicated smooth pattern generated by both architectures (blue: nonlinear dendrites, red: saturating synapses). (f-h): Learning of chaotic dynamics (Lorenz system), with a PCSN with nonlinear dendrites. (f): The spiking network imitates an example trajectory of the Lorenz system during training (blue); it continues generating the dynamics during testing (red). (g): Detailed view of (f) highlighting how the example trajectory (yellow) is imitated during training and continued during testing. (h): The spiking network approximates not explicitly trained quantitative dynamical features, like the tent map between subsequent maxima of the z-coordinate. The ideal tent map (yellow) is closely approximated by the tent map generated by the PCSN (red). The spiking network sporadically generates errors, cf. the larger loop in (f) and the outlier points in (h). Panel (h) shows a ten times longer time series than (f), with three errors.