Diffusion Lung Imaging with Hyperpolarized Gas MRI

Abstract

Lung imaging using conventional ¹H MRI presents great challenges due to low density of lung tissue, lung motion and very fast lung tissue transverse relaxation (typical T2* is about 1-2 ms). MRI with hyperpolarized gases (³He and ¹²⁹Xe) provides a valuable alternative due to a very strong signal originated from inhaled gas residing in the lung airspaces and relatively slow gas T2* relaxation (typical T2* is about 20-30 ms). Though in vivo human experiments should be done very fast – usually during a single breath-hold. In this review we describe the recent developments in diffusion lung MRI with hyperpolarized gases. We show that a combination of modeling results of gas diffusion in lung airspaces and diffusion measurements with variable diffusion-sensitizing gradients allows extracting quantitative information on the lung microstructure at the alveolar level. This approach, called in vivo lung morphometry, allows from a less than 15-second MRI scan, providing quantitative values and spatial distributions of the same physiological parameters as are measured by means of the “standard” invasive stereology (mean linear intercept, surface-to-volume ratio, density of alveoli, etc.). Besides, the approach makes it possible to evaluate some advanced Weibel parameters characterizing lung microstructure - average radii of alveolar sacs and ducts, as well as the depth of their alveolar sleeves. Such measurements, providing in vivo information on the integrity of pulmonary acinar airways and their changes in different diseases, are of great importance and interest to a broad range of physiologists and clinicians. We also discuss a new type of experiments that are based on the in vivo lung morphometry technique combined with quantitative CT measurements as well as with the Gradient Echo MRI measurements of hyperpolarized gas transverse relaxation in the lung airspaces. Such experiments provide additional information on the blood vessel volume fraction, specific gas volume, the length of acinar airways, and allows evaluation of lung parenchymal and non-parenchymal tissue.

Introduction

Decades ago, histological measurements of ex vivo lung specimens became the gold standard for identifying and quantifying the lung microstructure and changes associated with aging and diseases (1). However, these techniques only assessed limited portions of the lung and had the impractical requirement of ex vivo sampling. Recent advances in hyperpolarized gas diffusion MRI have led to developing a new approach to this problem – in vivo lung morphometry technique (2) – a method providing in vivo 3D tomographic information on the lung microstructure at the alveolar level from a fast (about 10-sec) experiment based on MRI measurements of hyperpolarized ³He gas diffusion in lung airspaces (3-6). Previous developments of computed tomography (CT) allowed for the noninvasive in vivo identification of lung tissue damage and the grading of its severity through the assessment of lung parenchyma tissue density (7-11), the structure of small conducting airways (12-14), and it also assesses air trapping associated with small airways disease (15). However, CT does not currently allows visualization of acinar airways (i.e., alveolar ducts and sacs) and their structure. These vitally important alveolated airways, located in the nine distal generations of the 24-generation pulmonary airway tree, occupy 95% of lung volume (16,17) and function as the major gas exchanging units of the lung. The major function of the lung is delivery of oxygen to the body and removing CO₂ from it. The efficiency of these processes through the lung airspaces to the blood vessel network occupying alveolar walls depends mostly on the structure, integrity and functioning of the pulmonary airway tree. The morphometry of the pulmonary acinus has been studied in numerous publications (e.g. (9,16-26)). These studies provided invaluable information on the lung microstructure that is the basis of the current knowledge on the lung structure and function. Such geometrical parameters as mean linear intercept (Lm), lung parenchyma surface-to-volume ratio (S/V) and number of alveoli per unit lung volume (N_v) are most commonly used to characterize the lung morphometry. Although the lung stereology has been in use for more than a half century and is considered a gold standard (see recent reviews (27,28)), the debates about its accuracy in estimating lung morphometry continue (29-36). This is mostly due to the objective problems of lung specimen preparation and the subjective bias in selection of “random” regions of lung parenchyma (1). However, the clinical and even research utility of the “standard” lung morphometry is limited by its invasive nature.

The rapid development during the past two decades of hyperpolarized ³He and ¹²⁹Xe gases MR imaging of lung air spaces has resulted from advances in the spin physics of optical pumping (37) and affordable high-power diode laser arrays. Even though these gases have four orders of magnitude smaller nuclear spin density (at standard pressure) compared to water (see Table 1), by using special laser equipment, they can be hyperpolarized to achieve a polarization almost five orders of magnitude more than the polarization of water protons at room temperature (37-41). This increase in polarization more than compensates for the decreased density of the gas and results in a very intense MRI signals from hyperpolarized ³He and ¹²⁹Xe gases, compared to those of water. This has opened the door to applications for which gaseous agents are uniquely suited, such as lung imaging. The MRI measurements with ³He and ¹²⁹Xe gases are safe and well-tolerated (42,43) and can be repeated in vivo on a regular basis to serve as a tool for research, clinical, and drug development studies. A substantial difference between these two gases is that ³He gas after inhalation remains in lung airspaces, while ¹²⁹Xe gas partially dissolves in lung tissue and blood.

Table 1.

Gyromagnetic ratios, γ, diffusion coefficients, D₀, and molar concentration, c, of water protons, ³He and ¹²⁹Xe gases at 37° C. Diffusion coefficients for ³He and ¹²⁹Xe gases are shown as diluted in air // 100% concentrated (197).

	γ, 108 T−1·sec−1	D0, cm2/sec	c, mol/L
1H (H20)	2.6751	~3·10−5	110
3He	2.0379	0.88//2.05	0.04
129Xe	0.7452	0.14//0.06	0.04

A number of different techniques for lung imaging with hyperpolarized gases has been proposed over two decades. Examples based on ³He include anatomical images of human lungs from healthy subjects (44) and patients with several types of lung pathology (45), anatomical imaging of the initial generations of airway tree (46-48), measurements of the local fractional ventilation (49), oxygen concentration (50,51) and the local ventilation–perfusion ratio (52). Due to “dissolvability” of the ¹²⁹Xe gas, it allows studying exchange processes between gas- and tissue-dissolved phases (53-57).

By no means is these an inclusive list of references and applications developed from the onset of hyperpolarized gas biological imaging (58). Our review is focused on one specific pulmonary application in hyperpolarized gas imaging - diffusion MRI.

2. Diffusion of Hyperpolarized Gases in Lung Airspaces

There are several major differences between water proton-based diffusion MRI and hyperpolarized gas–based diffusion MRI. While the water is naturally present in the biological tissues and offers researchers a free ride, the diffusion MRI with hyperpolarized gases is based on the measurements of the diffusion of the hyperpolarized gas that should be prepared and introduced in the lung airspaces before the experiment. This is usually done during a subject's inhalation and the whole measurement should be accomplished during a single breath-hold. Other major factors differentiating water-based and hyperpolarized gas-based diffusion MRI are differences in the nuclear polarization, density and, of course, the dramatic difference in their diffusion coefficients – the self-diffusion coefficient of the free water (about 3·10⁻⁵cm²/s) is four-five orders of magnitude smaller than the diffusion coefficients of gas (0.88 cm² /s for ³He and 0.14 cm² /s for ¹²⁹Xe – see Table 1). A very small diffusion coefficient of the water imposes challenges on the MR measurement hardware by requiring very strong field gradients and long diffusion times. Very large diffusion coefficients of gases impose another challenge – very short diffusion times though the strength of the gradient can also be a challenge.

Another important issue is a “non-renewability” of hyperpolarized gas magnetization during imaging. If in the water MRI, longitudinal magnetization consumed by RF pulses, recovers between repeated RF pulses due to the Boltzmann thermal kinetic processes (59), in the hyperpolarized gas MRI, a prior-prepared (hyperpolarized) very strong non-equilibrium magnetization is “consumed” by the repeated RF pulses. Hence, very low-flip-angle gradient echo sequences are usually used. Luckily, T2* of the hyperpolarized gases in human lung airspaces is usually long enough (e.g., 27 ms in Ref. (60), 32 ms in Ref. (61) for ³He measurements at 1.5T; and 50 ms for ¹²⁹Xe at 1.5T reported in Ref. (62)) which provides sufficient time in the pulse sequence for incorporating diffusion-sensitizing gradients.

Under these considerations, the simplest MR measurement of diffusion is the Stejskal-Tanner pulsed field gradient (PFG) experiment (63) in which a free-induction decay MR signal is subjected to a pair of two opposite-polarity gradient pulses (Figure 1) – the so-called diffusion-sensitizing gradients.

Figure 1.

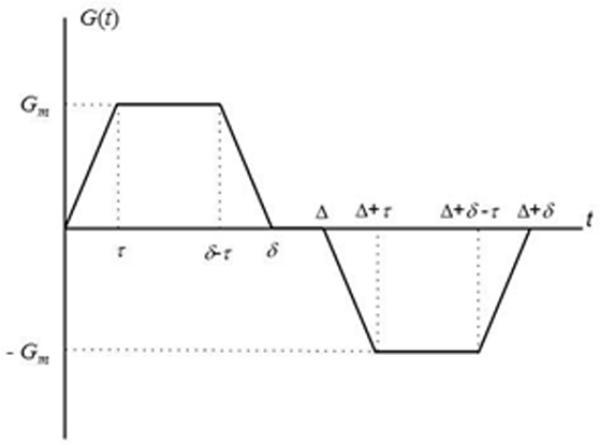
Diffusion sensitizing pulse gradient waveform employed in diffusion MRI with hyperpolarized gases at short diffusion times. In this diagram G_m is the gradient lobe amplitude, Δ is the spacing between the leading edges of the positive and negative lobes (usually called diffusion time), δ is the full duration of each lobe, and τ is a ramp-up and ramp-down time.

In the presence of gradient pulses, nuclear spins accumulate a net phase shift that depends on their initial positions and their displacements during and between pulses, resulting in incoherence of spins’ individual phases, hence decreased total signal amplitude. In the case of unrestricted diffusion, the MR signal S decays as

$$S=S_0\exp (-b{D}_0)$$ [1]

Here, S₀ is the MR signal intensity in the absence of diffusion-sensitizing gradients, the parameter D₀ is termed the free diffusion coefficient, and the b-value is determined by the gradient waveform shape. For the gradient pulses in Figure 1, the corresponding b-value is (3):

$$b={\left(\gamma G_m\right)}^2\left[{\delta }^2\left(\Delta -\frac{\delta }{3}\right)+\tau \left({\delta }^2-2\Delta \delta +\Delta \tau -\frac{7}{6}\delta \tau +\frac{8}{15}{\tau }^2\right)\right]$$ [2]

which is similar to a corresponding expression for a spin-echo-based approach (64).

In the presence of barriers such as alveolar walls and walls of lung airways, the diffusive motion is restricted and the MR signal can no longer be described in terms of Eq. [1]. In this case, the signal is often described by a phenomenological equation:

$$S=S_0\exp (-b\cdot ADC)$$ [3]

where ADC is a so-called Apparent Diffusion Coefficient. Contrary to the free diffusion case where ADC is equal to D₀ and depends only on the molecular diffusion properties, the ADC for restricted diffusion evaluated from Eq.[3] has usually a quite complicated dependence on the structure of restrictive barriers (tissue properties), the timing details of the gradient waveform and gradient strength in Figure 1.

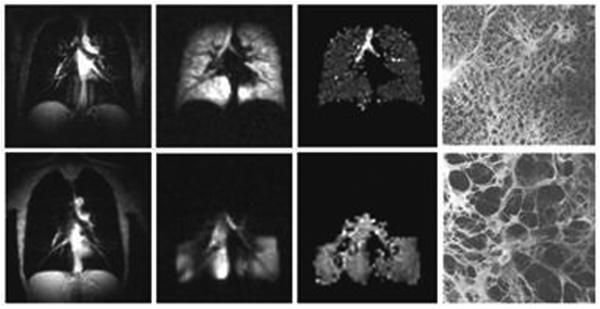
Examples of ventilation images (MRI-measured distribution of ³He gas inhaled by a subject) and ³He gas ADC maps, obtained using measurements with two b-values in Eq. [3], of normal human lungs and lungs with severe emphysema are shown in Figure 2. The remarkable differences in the ADC values between healthy (0.17 cm²/sec) and diseased (0.52 cm²/sec) lung indicate that diffusion imaging of the lung with hyperpolarized helium could provide a very sensitive tool for clinical evaluation of emphysema.

Figure 2.

Images of normal and emphysematous human lungs. Left to right– proton MRI, ³He ventilation maps, ³He gas ADC maps and histological slices (the latter adopted from (198)); first row - normal lungs, second row - lung with emphysema. ADC in a normal lung is rather homogeneous except for large airways (trachea and its first branches) and is about 0.17 cm²/s. In the emphysema lung ³He gas penetrates only into ventilated regions (lower portion of the lung in this case) and has an ADC about 3 times bigger (0.55 cm²/s) than the ADC in the normal lung.

3. Lung Morphometry with Hyperpolarized Gas Diffusion MRI – Theoretical Background

To advance diffusion measurements to research and clinical practice, a fundamental question – what salient features of lung microstructure affect diffusion measurements of ³He or ¹²⁹Xe gases – needs to be answered. To obtain quantitative information on lung microstructure at the acinar level, geometrical parameters describing the lung microstructure should be related to the parameters extracted from MR measurements independent of pulse sequence parameters and/or gas concentration. Obviously, such a complicated structure as lung cannot be analyzed without some simplifications and assumptions. To date several models for lung microstructure have been explored to simulate the diffusion attenuated MRI signal. A modified Weibel geometrical model of acinar airways (17,19) has been used in (2-5,65). Other examples include a porous media approach proposed by Mair et al (66,67); a cylindrical model with semi-spherical alveolar shape and two-dimensional grape-like structures used by Fichele et al (68); Kitaoka model (three-dimensional labyrinth filling a cubic volume (69)) used by Grebenkov (70); tree-like branching structures used by Verbanck et al (71,72), Perez-Sanchez et al (73), Conradi et al (74), and Bartel et al (75). Models based on morphological images or high-resolution X-ray tomography were used by Miller et al (76) and Tsuda et al (77). A geometrical model utilizing the Voronoi meshing technique (78) was simulated by Plotkowiak et al (79). These publications provided important insights into gas diffusion properties in lung airways, some of them were discussed in detail by Plotkowiak et al (79).

For these approaches to become a useful research and clinical tool in studying lungs in health and disease, they need to allow solution of the inverse problem – evaluation of lung geometrical parameters from specially designed MRI experiments. Such approaches should satisfy at least two requirements. They must reflect the salient features of lung microstructure geometry, which affects the MR signal formation, and the number of parameters characterizing the lung model should be small enough to be able to be determined from MR data. Currently there is only one approach that meets both the criteria– in vivo lung morphometry – that was developed in (2-5,65). It is based on a well-accepted Weibel geometrical model of lung microstructure at the acinar level that is based upon stereological methods (17,19), and the theoretical equations relating the MR diffusion-attenuated signal to the acinar airways geometric parameters. This approach allows evaluation of lung geometrical parameters from a rather simple and fast multi-b MR measurements (usually 5-6 b-values (3)). Theoretical parameters used in this approach also allow calculation of the standard lung morphological parameters analogous to those extracted from direct histological measurements, hence the term “in vivo lung morphometry”. Details on multi-b sequence requirements and optimization are provided in (5,65).

3.1 Weibel Geometrical Model of Lung Acinar Airways

To better understand the relationship between the measured ADC and lung microstructure at the alveolar level, we first need to describe lung in terms of some basic geometrical elements. The structure of lung airways is usually considered as branching tree (18) beginning at the trachea and leading through bronchi and bronchioles to the terminal bronchiole that feeds each acinus – the major gas exchange unit in the lung. In humans there are fourteen generations of airways prior to the terminal bronchioles and another nine inside the acinus, with an average acinar volume of about 187 mm³ (18). Gas ventilation in the trachea, bronchi, bronchioles and terminal bronchioles occurs by convection (bulk flow), while diffusion is the primary ventilation mechanism beyond the terminal bronchioles – in the acini, where about 90 to 95% of gas resides (80). The acinus is defined as a distal branch of airway tree that starts with a first order respiratory bronchiole. A large number of studies have been devoted to acinar geometry (see for example (17,81-83)). According to (17,19) essentially all airways in the acinus are decorated by alveoli forming an alveolar sleeve (see example in Figure 3) and participate in gas exchange (18).

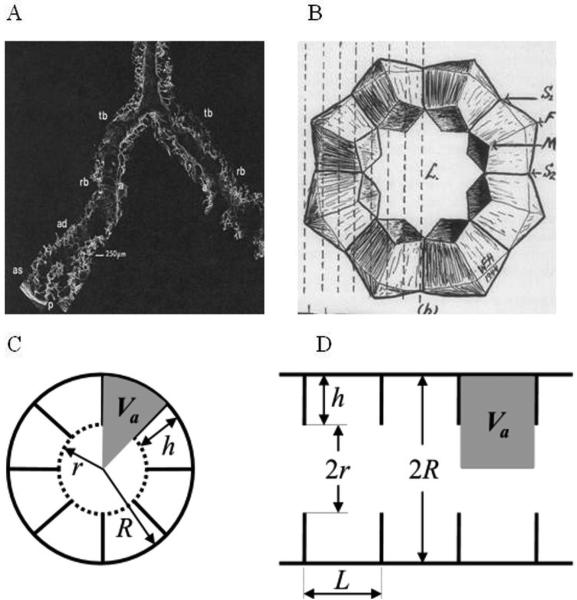
Figure 3.

Left upper panel: distal portion of airways as seen with SEM. Terminal bronchiole (tb), respiratory bronchiole (rb), alveolar duct (ad), alveolar sacs (as), and alveoli (a) are seen in continuity as the airway branches to the pleura (p) (adapted from (83)). Right upper panel: schematic drawing of acinar airway cross sections representing eight alveoli surrounding the lumen (L) (adapted from (84)). Lower panel: two cross sections (transverse, C, and longitudinal, D) of an acinar airway with eight alveoli distributed along the annular ring (eight-alveolar model) (2). Each airway (duct or sac) is considered geometrically as a cylindrical object consisting of an alveolar sleeve with alveoli opening toward the internal cylindrical air passage (lumen). The diagram defines inner (r) and outer (R) airway radii and effective alveolar diameter (L). The alveolar size L along the airway is assumed to be the same as in the cross-section, hence, L = 2Rsin(π / 8) = 0.765R. The depth of alveolar sleeve, h, is: h = R – r.

In humans, the intra-acinar airways branch dichotomously over about 9 generations. Both the internal acinar airway radius r and the outer radius R (including the sleeve of alveoli) vary depending on the position and branching level of the acinar airway tree; however, the variation is rather small – the distribution width for R is about 60 μm and for r is about 30 μm with mean values of 350 μm and 160 μm correspondingly (17). The “narrowness” of the distributions of parameters R and r creates a solid basis for characterizing acinar airways by the mean values of R and r.

Another important parameter in Figure 3 is the “effective alveolar diameter” L, which is not specified in (17). While numerous models have been proposed previously (see for example Fig. 41 in (16) and discussion therein), in our approach (2) we adopted an eight-alveolar model (84,85) in which each alveolus occupies 1/8 of the annular ring. In this model we also assume that the alveolar effective diameter L is equal to the length of the cord corresponding to 1/8 of the annular ring, L = 2R · sin(π/ 8)= 0.765 · R reducing the number of geometrical parameters in the model to only two: R, and the depth of alveolar sleeve h = R - r. Making the realistic assumption that lung volume scales as the cube of linear dimensions and scaling the values from (17) to a more typical volume of 0.6 TLC (Total Lung Capacity), the mean values of the parameters become R = 300 μm, r = 140 μm, and L = 230 μm, consistent with literature values for average alveolar diameter ranging from 200-260 μm (16,20-22). Models that instead contain four or six alveoli per annular ring would correspond to bigger alveolar diameters (472 and 314 μm, respectively) and are not compatible with the above mentioned experimental data.

Using these parameters, we can estimate the alveolar surface area S_a, lung volume per alveolus V_a, alveolar number density N_v – the number of alveoli per unit lung volume based upon geometry, and the mean linear intercept L_m (2):

$$\begin{array}{c}\hfill S_a=\frac{\pi }{4}R\cdot L+\frac{\pi }{4}h\cdot (2R-h)+2h\cdot L,V_a=\frac{\pi }{8}{R}^{2}L\hfill \\ \hfill L=2R\sin \frac{\pi }{8},N_v=\frac{1}{V_a},S∕V=S_a∕V_a=4∕Lm\hfill \end{array}$$ [4]

3.2. Anisotropic Diffusion of Gas in Acinar Airways

The diffusion time Δ in Eq. [2] is a crucial parameter. For in vivo lung morphometry Δ is selected such that the corresponding characteristic diffusion length L₁ = (2D₀Δ)^1/2 (rms free displacement in one direction) should be larger than the average alveolar radius but smaller than the mean length of alveolar ducts or alveolar sacs (in human lung, about 0.76 mm and 1 mm, correspondingly (17)). Hence, gas can diffuse out of alveoli and across the acinar airways in the time duration of the MR measurement but should remain mostly in the same alveolar duct or sac. This constraint allows us to consider acinar airways (respiratory broncheoli, alveolar ducts and alveolar sacs) rather than individual alveoli as the elementary geometrical units. Under these conditions, effects of branching structure of acinar airways play little role in diffusion MR signal formation (5) (see also detail discussion later in this review). For ³He gas these conditions restrict the diffusion time Δ in human lungs to about 2 ms (2,5) and for ¹²⁹Xe to about 10ms (65). In small animal lungs the diffusion time Δ should be order of magnitude shorter (65,86,87).

The alveolar walls as well as the walls of alveolar ducts and other branches of the airway tree serve as obstacles to the path of diffusing atoms and reduce the gas diffusivity. Crucially, these restrictions are substantially less along the airway axis than perpendicular to it; consequently, diffusion in the airway is anisotropic (3). Therefore, the ADC describing signal attenuation in a single airway depends on the angle α between the direction of the diffusion-sensitizing gradient G and the airway's principal axis:

$$S=S_0\cdot \exp (-b\cdot ADC\left(\alpha \right))$$ [5]

Due to the cylindrical symmetry of the airway,

$$ADC\left(\alpha \right)=D_L{\cos }^2\alpha +D_T{\sin }^2\alpha$$ [6]

where apparent diffusion coefficients, longitudinal D_L and transverse D_T, correspond to diffusion along the airway principal axis and in the transverse plane, respectively (3). Equation [6] is rather common in describing anisotropic diffusion in different tissues, e.g. (64,88).

With the spatial resolution of several millimeters currently available with ³He or ¹²⁹Xe MRI, each voxel contains hundreds of airways with different orientations. Due to the large number of acinar airways in each imaging voxel, their orientation distribution function can be taken as uniform, and the total signal S can be written as (3):

$$S\left(b\right)=S_0\exp (-b{D}_T){\left(\frac{\pi }{4b{D}_{AN}}\right)}^{1∕2}\cdot \Phi \left[{\left(b{D}_{AN}\right)}^{1∕2}\right],D_{AN}=D_L-D_T$$ [7]

where Φ(x) is the error function. This macroscopically isotropic but microscopically anisotropic model predicts non-exponential dependence of diffusion attenuated MRI signal on b-value. The validity of Eq. [7] was confirmed in vivo by experimental measurements in humans (2,3), canines (89), mice (86,87), and rats (90,91) using hyperpolarized ³He gas. It was also confirmed in humans (92) and rats (93) using hyperpolarized ¹²⁹Xe gas.

Importantly, the diffusivities D_L and D_T determined from the MR experiment depend on both lung microstructure and the details of the Stejskal-Tanner pulse sequence (4) (therefore they are termed “apparent” diffusivities, ADC). Although general expressions for D_L and D_T are unavailable, it was demonstrated by means of computer simulations (2,4,5,65) that in a physiological range of geometrical parameters r and R, and “realistic” gradients used in MRI experiments, a linear approximation with respect to b-values is sufficient to describe the dependence of apparent diffusion coefficients D_L and D_T on b-values:

$$\begin{array}{cc}\hfill D_L=& D_{L0}\cdot (1-{\beta }_L\cdot b{D}_{L0})\hfill \\ \hfill D_T=& D_{T0}\cdot (1+{\beta }_T\cdot b{D}_{T0})\hfill \end{array}$$ [8]

The dimensionless coefficients β_L and β_T reflect the non-Gaussian diffusion effects in each individual airway and are usually defined in terms of the so called kurtosis K – the second order term in the general cumulant expansion of the MR signal (e.g., (94-97)); (K_L = 6β_L, K_T = −6β_T). It should be noted that the signal S(b) in Eq. [7] also demonstrates “primary” non-monoexponentiality in b-value, which is due to orientation averaging of the signals from individual airways. The non-monoexponentiality in b-value described by the coefficients β_L and β_T is a feature of individual airways and is additional to this “averaging” effect.

The choice of diffusion time described above is very convenient for simplifying lung model by minimizing effects of branching structure of airway tree that would otherwise require numerous additional parameters. On the other hand, this choice of Δ is not convenient for developing analytical theory of gas diffusion since it places experimental conditions in the intermediate regime when neither short diffusion time nor long diffusion time approximations can be used. In (2), the apparent diffusion coefficients D_L and D_T characteristic of ³He gas diffusion in this intermediate regime were related to the geometrical parameters of acinar airways, R and r, in human lungs by using the method developed in (4). The method is based on Monte-Carlo simulations of ³He gas molecules diffusing in lung airways with geometry outlined in Figure 3.

Figure 4 illustrates typical dependences of the parameters D_L0 on the ratio h / R and the transverse diffusivity D_T0 on the ratio R / L₂ (2). The corresponding analytical equations describing dependencies of D_L and D_T on the geometrical parameters R and h (2) are provided in the Appendix (Eqs. [18]-[19]).

Figure 4.

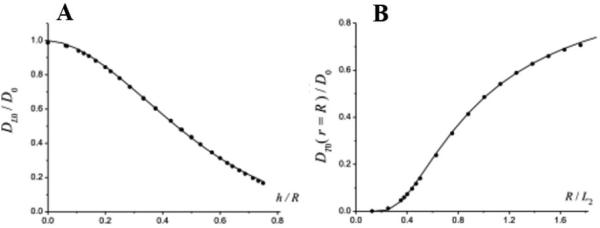
(adapted from (2)) Plots representing data obtained by Monte-Carlo simulations (symbols) of the parameters (A) D_L0 as functions of h/R and (B) D_T0 on the ratio R/L₂. Solid lines are calculated according to Eqs. [18]-[19].

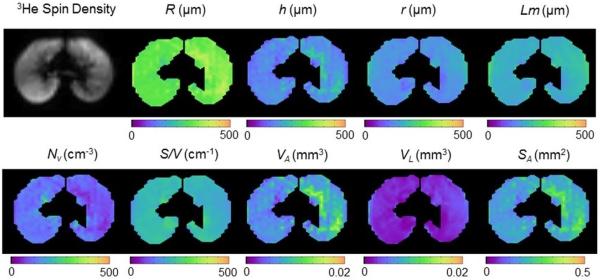
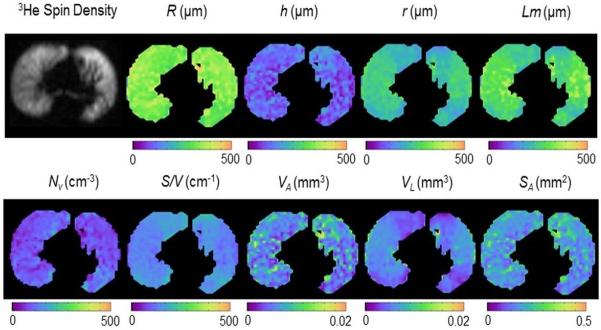
Fitting Eqs. [7]-[8] and [18]-[19] to multi-b measurements of the ³He diffusion-attenuated MRI signal in lung airways on a voxel-by-voxel basis makes it possible to evaluate the mean geometrical parameters for lung acinar airways (in spite of the airways being too small to be resolved by direct imaging). As a result, parametric maps for airway radii R and alveolar depths h and physiologically important parameters Lm, S/V and N_v can be generated (see example in Figure 5).

Figure 5.

Example of lung morphometry parameter maps from the central axial slice of a 19-year old subject.

It is important to emphasize that the phenomenological expressions, Eqs. [18]-[19], are not universal, they are derived for specific values of model parameters and diffusion time Δ. Namely, they are valid with accuracy of a few percent for Δ =1.5–2 ms and R = 280–400μm (5). This interval of R covers both the typical radii of acinar alveolar ducts in healthy human lungs and those in lungs with mild emphysema. For larger R corresponding to lungs with advanced emphysema our approach can produce larger estimation errors and the Weibel geometrical representation of lung airways used in our approach also may become inadequate due to lung tissue destruction. For airway sizes characteristic of small animal lungs (mice, rats), where a typical radius is substantially smaller (R ~ 100μm) a modified version of Eqs. [18]-[19] were derived (86) for the diffusion time Δ = 0.3–0.4 ms, see Eqs. [23]-[24] in Appendix.

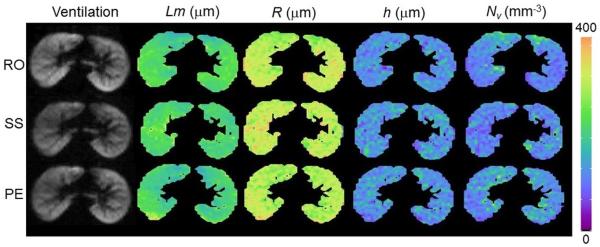
One of the important assumptions of the model in Eq. [7] is the macroscopically isotropic distribution of acinar airways directions. Specifically, with the imaging resolution currently achievable, we assume that the acinar airways are isotropically distributed in direction over a given imaging voxel (3). This simplification is supported by the random appearance of alveoli on histology sections (16) and assumes that the MRI signal has a negligible contribution from the 5% of gas that lies in the conducting airways (80). To further test this hypothesis, we collected data with three directions of diffusion-sensitizing gradients along different anatomical directions (98). Results are presented in Figure 6 demonstrating validity of our assumptions.

Figure 6.

(adapted from (98)) Comparison of several parameter maps from the central slice in a healthy subject, acquired with the diffusion gradient oriented along the readout (RO), slice select (SS), and phase encoding (PE) directions. Maps acquired at different directions show very little differences: the average % coefficient of variation (% CV) is 2.6% for Lm, 1.7% for R, 1.7% for h, and 1.9% for N_v.

3.3. Effects of Acinar Airways Branching and Distribution of Geometrical Parameters

Questions related to “theoretical accuracy” of lung morphometry technique were discussed in detail by Sukstanskii et al in (5). As for any approach dealing with a complicated structure, the lung morphometry technique with hyperpolarized gas diffusion MRI is based on assumptions and simplifications that potentially might bias the measurements. The core of the technique is a model that incorporates the salient feature of gas diffusion in acinar airways on the time scale when diffusing gas molecules have a chance to diffuse in and out from single alveoli but still spend most of their time in the same acinar airway. This leads to diffusion being anisotropic on microscopic (single airway) scale – the diffusivity D_L along airway axis is bigger than the diffusivity D_T perpendicular this axis. This microscopic anisotropy has been confirmed in numerous publications (2,3,86,87,89-93). Since the measured MR signal originates from a large number of acinar airways with almost homogeneous distribution of their direction, diffusion MR signal has very little dependence on diffusion sensitizing gradient direction, i.e. it has macroscopically isotropic character – see experimental validation in (98) and Figure 6 above.

To further address the accuracy of this theoretical model, Sukstanskii et al (5) conducted Monte-Carlo simulations of gas diffusion in lung acini in a more general model, accounting for (a) the branching structure of the acinar airways and the finite length of alveolar ducts and sacs, (b) the distribution of airway geometrical parameters R and r of 17% about the mean values, and (c) the effects of internal inhomogeneous magnetic fields. These results were then fitted by the model in Eqs. [7]-[8] and [18]-[19].

Simulations were conducted for diffusion time Δ = 1.8 ms used in ³He lung morphometry technique in humans (2). For this short diffusion time the probability to cross two branching nodes and to diffuse into the next-to-adjacent airway is negligibly small – about 1%. Hence it is sufficient to consider for simulations only two types of basic airway configurations as shown in Figure 7 and weight them appropriately for calculating MRI signal. Of course, such a simplification is not valid for long diffusion times.

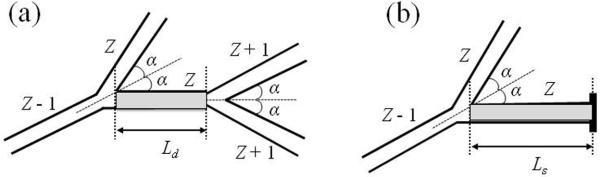
Figure 7.

Two types of basic airway configurations contributed to MRI signal (5). The internal alveolar structure of the airways is not shown and the aspect ratio is changed for better view of the structures. The first configuration with two nodes (Figure 7a) corresponds to an alveolar duct of generation Z (shaded airway), surrounded by a “parent” duct of generation (Z − 1), a “sister” airway of generation Z, and two “daughter” airways of generation (Z + 1). Symmetrical branching with half-angle α = 40° is assumed. The second configuration with one node (Figure 7b) corresponds to an alveolar sac of terminal generation Z (shaded airway), surrounded by a “parent” duct of generation (Z − 1) and a “sister” airway of generation Z.

As demonstrated in (5), all the parameters (R, r, S/V) found from fitting the model to simulated data using Eqs. [7]-[8] and [18]-[19] representing an idealized structure of branching acinar airways, are very close to the input values. In particular, for the surface-to-volume ratio, the average difference is 6.5% which is smaller than differences in results obtained by direct histology due to different issues related to sample preparation (1).

One of the main assumptions of the model was the ability to describe the total MR signal from an acinus as the sum of signals from individual acinar airways. This assumption holds only if a diffusing ³He atom resides primarily within the same airway throughout the diffusion gradient pulse. Our simulations demonstrate that indeed, most walkers spend most of their diffusion time (typically, 75%) within a single airway. This explains why our approach, based on the assumption of “non-communicating” or infinite-length airways, describes data very well.

In (5), the effect of the susceptibility induced internal inhomogeneous magnetic field on the parameter estimate was also analyzed. This field depends on the geometry of the septa forming alveoli and the susceptibility difference Δχ between the septa and the lung airspaces. For the Weibel model of acinar airways shown in Figure 3, the magnetic field has been calculated analytically by solving Maxwell's equations and taking into account that the thickness of alveolar septa, d, is much smaller than R and r. Assuming that Δχ = 9 ppm (as for water/air interface, SI units) and the septa thickness d = 10 μm (16,26), it was evaluated that the effect of the internal filed is rather small: the relative errors for the parameters R, r, and Lm at B₀ = 1.5T is smaller than 1% and for B₀ = 3T could reach 4%. A small predicted difference between 1.5T and 3T measurements was recently confirmed by Paulin et al (100). However, our estimates of the relative errors for B₀ = 3T are smaller than those found in (99). In contrast to diffusion properties, the induced field is sensitive to the geometry of alveolar septa. A slight deviation from idealized smooth geometry of alveolar walls leads to increase of the internal field. This can be effectively described by introducing an apparent septa thickness d_app. For example, for d_app = 20 μm, the relative error for Lm can reach 1.5% at B₀ = 1.5T and 9% at B₀ = 3T. These are close to those reported in (99).

4. Validation of ³He Lung Morphometry Technique

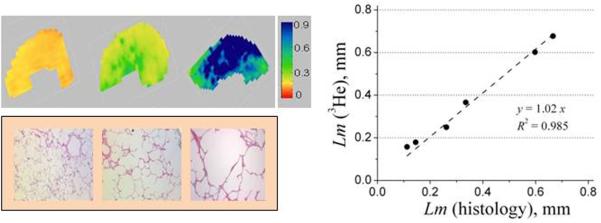
In (2) the MRI-based measurements of lung morphometric parameters were validated in explanted human lungs against direct invasive morphometric measurements, the current gold standard. The results, shown in Figure 8, demonstrate images of Lm in healthy lungs and lungs with different levels of emphysema (mild, moderate, and severe). Figure 8 also demonstrates an excellent agreement between direct histological and ³He-based measurements of Lm. It should be noted that the MRI experiment provides for much higher statistical power since the data are collected from thousands of voxels as compared to very few regions (twenty to forty) from histological cores.

Figure 8.

(adopted from (2)) Upper row: examples of the Lm (in mm) maps obtained from normal human lung (left) and lungs with different stages of emphysema (mild - middle and severe - right). Lower row: examples of histological slices obtained from the same lungs as above. Right panel: plot of mean linear intercept obtained by means of lung morphometry with hyperpolarized ³He diffusion MRI vs. direct measurement.

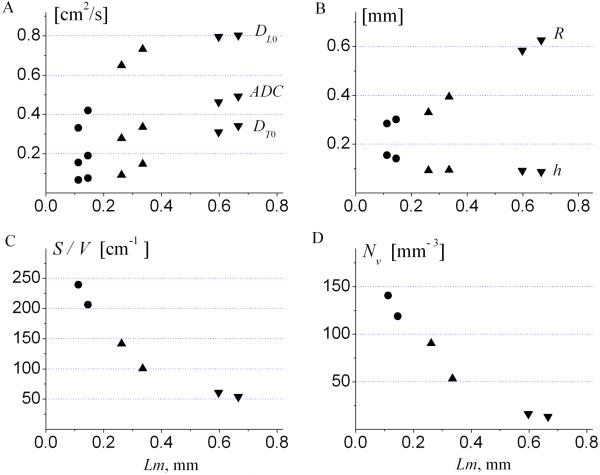
The variation of ADC, anisotropic diffusion coefficients (D_L0 and D_T0 from Eqs.[18]-[19]) and acinar airway geometrical parameters with histological emphysema severity, obtained from six lung specimens (2), are shown in Figure 9.

Figure 9.

(adopted from (2)) Summary of data obtained for six human lung specimens. Markers (•) represent two control healthy lungs, markers (▲) – two lungs with mild emphysema, markers (▼) – two lungs with severe emphysema. Each data point is a median calculated across all imaging voxels for a given lung specimen. Horizontal axis is the mean Lm obtained from direct histological measurements on the same lungs.

Figure 9a demonstrates that the longitudinal diffusivity D_L0 grows rapidly at initial stages of emphysema and soon approaches the “free” limit (about 0.88 cm²/s) for severe cases. Such a behavior is the result of reduced alveolar sleeve depth h with emphysema progression, as seen in Figure 9b. This destruction or retraction of the septa separating alveoli belonging to the same airway leads to lessening the restrictions to ³He gas diffusion along (parallel to) airways, practically removing them in severe emphysema cases. Figure 9b demonstrates that the major decrease of alveolar depth occurs already at the initial stages of emphysema – between normal and mild stages. At the same time, the airway radius R grows substantially with emphysema progression, reflecting tissue dilation and alveolar destruction and coalescence. The mechanism of “dilation of alveolar ducts with retraction of alveolar walls” was first suggested decades ago to describe the microscopic appearance of emphysema in human lungs (84) and was later confirmed in elastase-induced emphysema in rodents (102,103). More recent studies (104) also demonstrated shortening of alveolar walls and effacement of inter-alveolar septa. The results in (2) observed this phenomenon by a non-invasive technique for the first time and quantified such changes with emphysema progression.

The results for surface-to-volume ratio from diffusion MRI shown in Figure 9c are in good agreement with the results of morphometric measurements (9) obtained from excised lung specimens: S / V = 256±24 cm² /ml for control human subjects, 165 ± 23 cm² /ml for subjects with mild emphysema, and 43±6 cm² /ml cm²/ml for severe emphysema.

Measurements of N_v in two healthy lung specimens (120 and 146 per mm³) in Figure 9d are in agreement with a direct morphometric approach (21) in healthy human lungs (the average N_v varies between 132 and 177 per mm³). In addition to the above-cited measurements in healthy lungs, data in Figure 9d demonstrate changes in the number density of alveoli with emphysema progression – N_v decreases to about 60 per mm³ in mild emphysema and even further to about 10 per mm³ in lungs with severe emphysema. Such decreases in alveolar density are expected due to lung dilation and alveolar coalescence.

Osmanagic et al (86) applied the lung morphometry technique with hyperpolarized ³He diffusion MR to study explanted lungs in mice. The MR protocol and empirical relationships relating diffusion measurements to geometrical parameters of lung acinar airways were adjusted to acquire data with much shorter diffusion times as compared to humans to accommodate the substantially smaller acinar airway length. This measurements yielded mean values of lung surface-to-volume ratio of 670 cm⁻¹, alveolar density of 3200 per mm³, alveolar depth of 55 μm and mean chord length of 62 μm, all consistent with various results from the literature obtained by stereological analysis of mouse lungs (35,105-112). The technique was further implemented by Wang et al (87) for in vivo lung imaging in mice. Results indicated a very good agreement between in vivo morphometry via ³He MRI and microscopic morphometry after sacrifice.

5. Reproducibility of in vivo Lung Morphometry

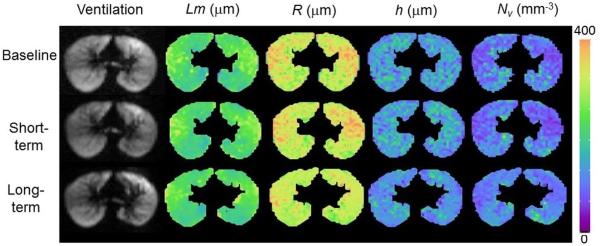
The reproducibility of lung morphometry to detect changes during longitudinal studies and therapeutic trials was established by Quirk et al (98). A total of seventeen lung morphometry measurements were performed on five healthy adult subjects to assess short- and long-term reproducibility and sensitivity to the orientation of the diffusion gradients. Results for the latter are presented in Figure 6. The reproducibility results are presented in Figure 10 and Table 2.

Figure 10.

(adapted from (98)) Example of short-term (same day) and long-term (four month) reproducibility of helium lung morphometry measurements over the central slice for a healthy subject.

Table 2.

(adapted from (98)). The average % coefficient of variation (% CV) for selected lung morphometry measurements in healthy subjects across repeated scans.

	Lm % CV	R % CV	h % CV	Nv % CV
Same Day Reproducibility	2.1%	0.8%	2.0%	2.0%
Long Term Reproducibility	2.9%	1.6%	3.1%	3.5%

The values of all lung morphometry parameters demonstrate a high degree of reproducibility both during different inhalations on the same day and months apart. The images in Figure 10 show the reproducibility of parameter maps for Lm, R, h, and N_v over the short term (same imaging session), long term (four months), and across diffusion gradient orientations in a healthy subject. The % coefficient of variation (% CV) averaged across subjects is shown in Table 2. While there are subtle differences in the parameter maps in Figure 10, these effects are small compared to natural variation across the lung. The independence of lung morphometry parameters to the direction of the diffusion gradient allows us to acquire data along only a single diffusion direction, thereby significantly decreasing the imaging time required. Together, this provides confidence for the use of ³He lung morphometry to detect changes during longitudinal studies and clinical trials.

6. Parallel Imaging of Hyperpolarized Gas in Lungs

Parallel imaging is particularly suitable for hyperpolarized gas MRI as the reduced number of total excitations allows for a higher flip angle in each RF excitation, which results in a higher SNR in each individual k-space acquisition (113). Parallel imaging can be used to reduce scan time in MRI, leading to increased lung coverage, shorter breath-holds which makes study accessible to more patients and reduces movement artifacts.

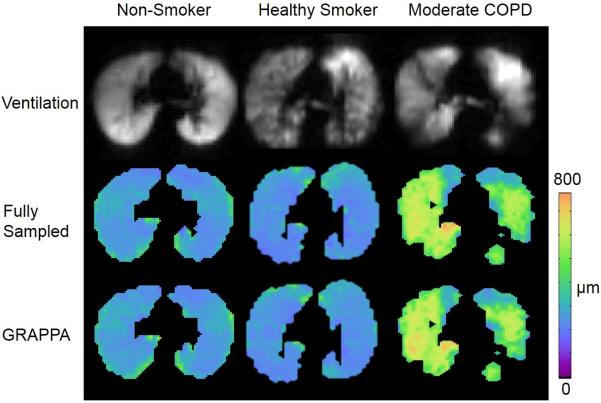
Example of applications to in vivo lung morphometry technique (114) is shown in Figure 11. Fully sampled and under-sampled multi-b diffusion data were acquired from human subjects using an 8-channel ³He receive coil. A parallel imaging reconstruction technique (GRAPPA) (115,116) was used to reconstruct under-sampled k-space data. For the GRAPPA acquisition, the effective acceleration factor was 1.74, the imaging time was reduced from 9.4 seconds to 5.4 seconds, and the flip angle was increased from 5.5° to 7.3 °.

Figure 11.

(adapted from (199)) Ventilation images and maps of the mean linear intercept Lm from the fully sampled (FS) and GRAPPA acquisitions on healthy and COPD subjects. No obvious differences were observed between the Lm maps of fully-sampled and under-sampled images, and regional features were all well preserved.

The distributions and magnitudes of lung morphometry parameters were highly consistent between the fully sampled and GRAPPA acquisitions. Figure 11 illustrates the ventilation images and maps of the mean linear intercept Lm obtained by means of the fully sampled and GRAPPA acquisitions on healthy and COPD subjects.

These results indicate that the lung morphometry measurement can be accelerated using parallel imaging with no significant difference from the fully sampled images: as demonstrated in (114), the average difference in parameters estimate was about 1%. The changes in these parameters caused by under-sampling in k-space are very small compared to the heterogeneity across the lung and the pathological changes in COPD (2,117). GRAPPA is a promising technique to significantly reduce imaging time and/or to improve the coverage for measurements of lung morphometric parameters with hyperpolarized ³He diffusion MRI with no significant difference in the measurement of lung morphometry from the fully sampled images.

7. Application of in vivo Lung Morphometry to Study Human Lungs

7.1. Changes in Lung Microstructure throughout Adult Lifespan

Lung function declines with aging in healthy individuals (118,119) and this process accelerates in diseases such as COPD (13,24,120). However, little information exists on the structural changes responsible for this decline (121). We used ³He lung morphometry to noninvasively detect age-dependent differences in acinar microstructure in healthy human subjects (122). Since structural changes are also known to occur in different lung diseases, establishing this age-dependent baseline is essential for accurate detection and differentiation of pathological changes.

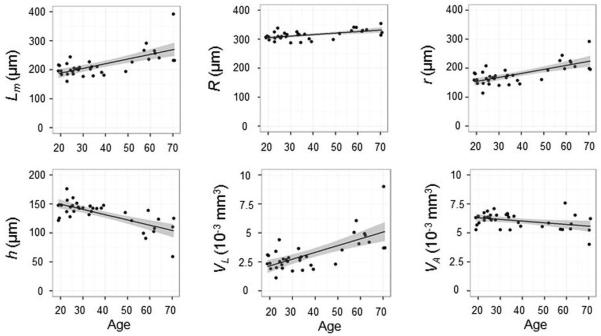
The study enrolled 36 adult healthy never-smokers. In older subjects there is a significantly increased acinar airway radius and decreased alveolar depth, as shown in Figure 12 and Figure 13. The observed trends in the changes of the acinar structure with aging occurred in the same direction but with smaller magnitude than those associated with the initial changes of emphysema (117) and are consistent with the proposal that COPD is a disease of accelerated lung aging (118). All of the lung morphometry parameters except for alveolar volume (V_A) were found to depend significantly upon the age of the study participant, but not upon race, weight, height, or gender. Figure 12 also demonstrates significantly increased heterogeneity across the lung with aging for most parameters. The values and age-dependence of the lung morphometry parameters are in good agreement with invasive histology measurements (17,21,123-126). Though the findings of increased Lm with aging by histology are sometimes interpreted as increases in alveolar size (123), the current results suggest instead that the alveolar volume (V_A) is similar in young and older subjects and that it is the acinar airway lumen that increases in volume with age (V_L).

Figure 12.

Example of lung morphometry parameter maps from the central slice of an older 62 year old healthy participant. Comparison with images in Figure 5 illustrates the shifts in parameter values and an increased heterogeneity in older subjects.

Figure 13.

Correlation of lung morphometry parameters with age in healthy subjects (all P < 0.05 except V_A). The lines are linear fits with 95% confidence intervals (shaded).

This cross-sectional study provides a first non-invasive insight into the differences in acinar airways structure associated with aging in a healthy adult population. ³He lung morphometry detected significant age-related differences of acinar structure in our healthy participants.

Substantial age-related changes in S/V from 209 to 152 cm⁻¹ occur, even in healthy subjects. This data (122) also demonstrated that, contrary to previous beliefs, the alveolar volume, V_A, actually decreased by 12% with increasing age. Alveolar depth decreased from 150 to 104 μm. Acinar airways expansion was mostly due to an increase (almost doubled) of the acinar airways lumen volume, V_D. Our results also establish a baseline of age-dependent lung parameters for use in future studies to detect pathologic changes.

7.2. Early Emphysematous Changes in Lung Microstructure of Current and Former Smokers

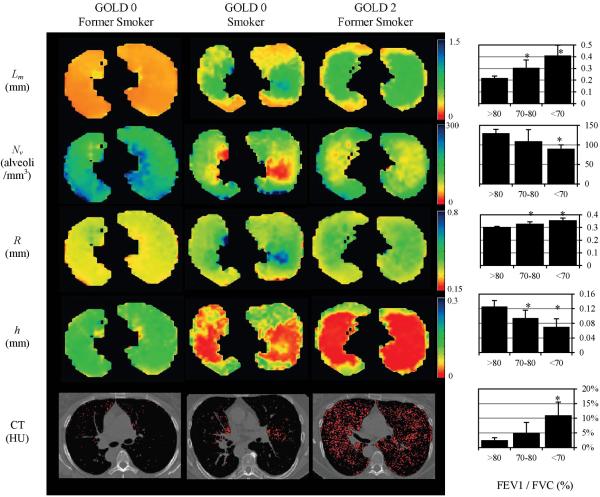
Quirk et al (6) used the in vivo ³He lung morphometry technique to quantitatively characterize early emphysematous changes in lung microstructure of current and former smokers. Thirty subjects with over 30 pack-year histories and mild or no abnormalities on PFT were studied. The results were compared against clinical standards: pulmonary function tests (PFT) and low-dose computed tomography (CT). Results (see Figure 14) demonstrate that the non-invasive ³He lung morphometry detected alterations in acinar structure in smokers with clinically normal PFTs. Compared to smokers with the largest FEV₁/FVC values, those with COPD had statistically significantly reduced alveolar depth (0.07 vs. 0.13 mm) and enlarged acinar ducts (0.36 vs. 0.30 mm). The mean alveolar geometry measurements in the healthiest subjects were in excellent quantitative agreement with literature values obtained using invasive techniques (R =0.30 mm, h =0.14 mm, at 1L above FRC (17)). Importantly, ³He lung morphometry detected greater abnormalities than either PFT or CT.

Figure 14.

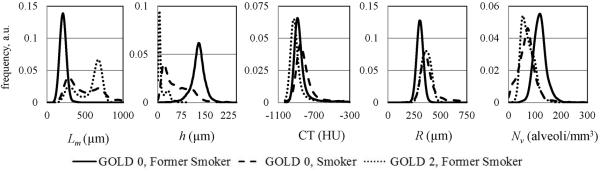
(adapted from (6)) Examples of the maps of acinar airways geometric parameters obtained with ³He lung morphometry and CT images for a GOLD 0 former smoker (left, FEV₁ = 93% predicted, FEV₁/FVC = 80%), a GOLD 0 smoker (middle, FEV₁ = 94% predicted, FEV₁/FVC = 71%), and a GOLD 2 former smoker (right, FEV₁ = 62% predicted, FEV₁/FVC = 56%). These images illustrate the heterogeneity of disease across the lungs and the significant increases in R and L_m, and decreases in h and N_v with COPD. Red pixels on the CT images indicate regions of emphysema (attenuation less than −950 HU). Charts on the right summarize results obtained from thirty current and former smokers; they show the increase in (a) mean chord length, (b) % EI₋₉₅₀, and (c) acinar duct radius, and decrease in (d) alveolar depth h with decreasing pre-bronchodilator FEV₁/FVC by PFT. The FEV₁/FVC < 70% group is statistically significant against all other groups for all measurements shown (*, P < 0.05). The FEV₁/FVC 70-80% group is also statistically significant against all other groups on the ³He lung morphometry measurements (*, P < 0.05), but not on the CT-based %EI₋₉₅₀. Error bars are standard deviations.

The important feature of all these maps is their relative homogeneity in normal lungs vs. significant disease-related heterogeneity in even early emphysema. In the latter case a clear contrast is seen between central portion of the lung and lung periphery. This “bipolar” behavior (two-peak feature) is especially obvious if data are presented as histograms, as in Figure 15.

Figure 15.

Histograms of the lung geometrical parameters and CT images in HU for the subjects in Figure 14.

We note that while lung density reflected in CT histogram is different in emphysema as compared to normal lungs, the relative shift in practically all parameters determined by ³He MRI is substantially larger. Probably the most interesting is behavior of Lm that demonstrates a pronounced “bipolar” feature that is also seen in alveolar depth histogram and only hinted in other ³He-derived parameters, but is not seen in CT data at all.

7.3. Lung Heterogeneity in COPD Differentiates Normal Aging from Accelerated Aging with Emphysema

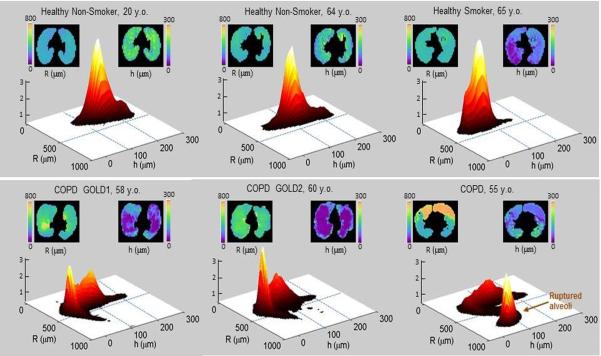
Results shown in Figure 5 and Figure 12 show rather homogeneous distribution of morphometric parameters in healthy human lungs. At the same time, the results in Figure 14 demonstrate substantial heterogeneity in lungs with emphysema. To further investigate the role of heterogeneity effects, in Figure 16 we show examples of data obtained from two “healthy” non-smokers (never smokers), one “healthy” smoker, two subjects with smoking-related COPD, and one with emphysema but without COPD. The 2D R-h histograms in both healthy non-smokers demonstrate rather sharp single peaks, though the position of the peak value in the 64-year old subject is shifted to the smaller h values (i.e., slight shallowing of acinar airways) as compared to the 20-year old (see airway illustration at right). This example demonstrates a “normal aging” process. However, in the healthy 65 y.o. smoker, the peak shifts further to smaller h (further shallowing of acinar airways), suggesting that smoking-induced “accelerated aging” has occurred. In patients with COPD, this peak not only shifts to the left, but also becomes smaller indicating a reduced portion of “normally-aged” lung; at the same time a new peak with a substantially smaller (almost vanishing) h appears, and this corresponds to the lung tissue that has practically “sleeveless” acinar airways (left peaks in GOLD1 and GOLD2 patients; the abbreviation “GOLD” stands for the “Global Initiative for Chronic Obstructive Lung Disease” (127); GOLD1, GOLD2, etc. characterize the severity of the disease). The last subject (“COPD”, 55 y.o.), known to have severe emphysema on CT (but a lack of COPD on spirometry), shows even more dramatic changes corresponding to the breakdown of airway walls. Indeed, his 2D R-h histogram has two peaks with one similar to normal radius airways (R about 300 μm) and the other similar to ruptured airways (R about 800 μm). The ³He morphometry clearly shows dramatic destruction of a portion of the lung in this subject (upper areas in the maps in Figure 16) and demonstrates the high sensitivity of the technique.

Figure 16.

Healthy aging vs. accelerated aging with smoking and COPD. Each figure-set represents data for an individual subject (total 6 subjects). In each set, the upper left figure is a map of acinar airway radii (R), the upper right figure is a map of acinar airways alveolar sleeve depth (h), and the lower figure is a 2D R-h histogram that reflects relative lung volume (vertical axis, arbitrary units) and corresponds to given R-h values (see definition in Figure 3). In all histograms, the peaks corresponding to R < 500 μm relate to portions of the lung without ruptured airways walls. In the 3 subjects in the upper row, these peaks represent “healthy aging” lung defined by slight shallowing of alveolar sleeve. In the two bottom row left subjects that have COPD with GOLD1 spirometry and GOLD2 spirometry severity, the left peaks correspond to the emphysematous changes where acinar airways are characterized by a dramatic shallowing of alveolar sleeve. In the bottom row right COPD subject, the peak at R > 500 μm corresponds to severely damaged portions of the lung that have had inter-airway walls breakdown (orange color in the R map). The bottom row COPD patients, from left to right, have age 58 y.o., 60 y.o., and 55 y.o., FEV₁/FVC 0.70, 0.63, and 0.71, and FEV₁% of the predicted normal value of 94%, 59%, and 90%, respectively. The top row right 65 y.o. healthy smoker has FEV₁/FVC 0.75 and FEV1% predicted 65%. The two upper row left healthy non-smokers (never smokers) have normal spirometry.

These results support the use of quantitative characterization of the normal aging process with mean (or median) values of morphometric parameters. However, the bi-modal structure of the histograms for people that have emphysema and COPD seen in Figure 16 demonstrates that the mean values of morphometric parameters do not sufficiently characterize the disease or its progression. This notion has significant implications for the development of unique phenotypes related to lung aging and disease (COPD/emphysema).

In vivo ³He lung morphometry was used by Paulin et al (100) to estimate the alveolar dimensions in a group of elderly healthy never-smokers and ex-smokers with and without emphysema. They found significant differences in never- and ex-smokers in acinar duct internal radius r and alveolar depth h, thus demonstrating a sensitivity of MRI noninvasive measurements to differentiate the effects of smoking and aging on acinar morphometry.

7.4. Tissue Damage Load Provides Quantitative Measure of Heterogeneous Lung Tissue Destruction

Based on the need for additional metrics of lung structural changes described above, we introduce Tissue Damage Score (TDS) and Tissue Damage Load (TDL) indices of lung tissue damage that address these bi-modal and other heterogeneous changes in lung tissue structure:

$$TDS=\frac{ControlPeakValue-VoxelValue}{ControlPeakValue},TDL=v\cdot \sum TDS$$ [9]

where v is an imaging voxel volume. TDS and TDL can be introduced for any morphometric parameter and are calculated based on the parameter's histogram. An example for S/V calculations is shown in Figure 17. TDS ranges from zero for normal lung tissue to one for totally damaged tissue (Voxel Value = 0). The sum in Eq. [9], resulting in the TDL, is over all voxels with “damaged” lungs that we define as all voxels to the left of the leftmost vertical brown line (PeakValue – 1.96· STD) in Figure 17. These indices are similar to those we have successfully used to quantify tissue damage in Multiple Sclerosis (128-130). Figure 18 shows substantially better differentiation between different subtypes based on TDL than on mean values of S/V measurements.

Figure 17.

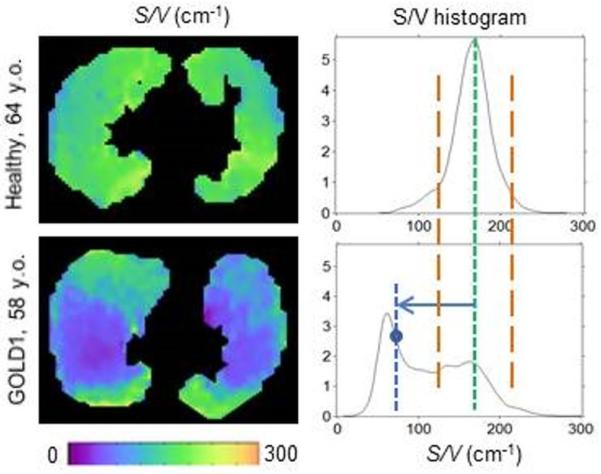
Example of S/V data obtained from a healthy (control) and a COPD GOLD1 subject (same as in Figure 16). Left figures show S/V maps, right figures show histograms of S/V distribution over three imaged slices. A green vertical line shows position of the Peak Value in the S/V distribution in healthy control subject. In COPD subject, this peak becomes smaller and shifts to the left; at the same time, a new peak at the left with substantially smaller S/V values is forming corresponding to the lung tissue with extremely shallowed (but not ruptured) acinar airways. Vertical brown lines show positions equal to PeakValue ± 1.96 · STD. The area between them would correspond to the 95% of the total area for a normal distribution. Even though our distributions are not normal, we select these boundaries to separate normal from abnormal tissue. The horizontal arrow shows an example of the difference between the control peak and a voxel value (as in Eq. [9]).

Figure 18.

S/V and TDL data obtained from a group of 14 young (age 20-30 years) healthy never-smokers, and four older (age range of 55-65 years) groups of subjects: 6 “older” healthy never smokers, 22 healthy smokers, 5 subjects that have smoking-related COPD GOLD1 (by spirometry) and 3 subjects that have smoking-related COPD GOLD2 (by spirometry). Each bar shows mean and STD values. Left bar-graph shows results for S/V within each group; right graph shows results for TDL. TDL for young healthy never-smoking control subjects was calculated based on their cumulative histogram. TDL for all groups in 55-65 y.o. categories was calculated based on the cumulative histogram of older healthy never-smoking control subjects.

7.5. In vivo Lung Morphometry of Lungs after Pneumonectomy

Different lung diseases sometimes require pneumonectomy – removing one of the lungs or lung lobes. After removal of a lung, the remaining lung usually increases in size to fill the space in the thoracic cavity. While the extent of this increase depends on the shifting of other organs, primarily the heart and liver, some degree of expansion is commonly noted. When the lung increases in size, it is uncertain whether this is the result of stretching of the existing alveoli, the growth of new alveoli, or a combination of both effects. If the lung responded purely by stretching, we would expect that the number of alveoli would be the same as for a single lung, the alveolar number density N_v would decrease, and the values of R and Lm would be elevated. A recent study by Butler et al (131) using helium lung morphometry found that a woman 15 years post-pneumonectomy had normal values for R with a uniform distribution of values across the lung, and slightly decreased values for h. These results suggest that the lung responded to the mechanical forces by forming new alveoli. These results were supported by Wang et al (132) in a longitudinal mouse study where compensatory growth was found to restore the lung volume, compliance, and alveolar number to pre-surgery values by a month following surgery.

7.6. Morphometric changes in the human pulmonary acinus during inflation

Hajari et al (133) used in vivo lung morphometry to study the mechanisms of lung inflation and deflation in humans. In spite of decades of research, there is little consensus about whether lung inflation occurs due to the recruitment of new alveoli or by changes in the size and/or shape of alveoli and alveolar ducts. In this study Hajari et al measured the average alveolar depth and alveolar duct radius at three levels of inspiration in five healthy human subjects and calculated the average alveolar volume, surface area, and the total number of alveoli at each level of inflation. The results indicated that during a 143±18% increase in lung gas volume, the average alveolar depth decreases 21±5%, the average alveolar duct radius increases 7±3%, and the total number of alveoli increases by 96±9% (results are means ± SD between subjects). These results indicated that in healthy human subjects the lung inflates primarily by alveolar recruitment and, to a lesser extent, by anisotropic expansion of alveolar ducts.

8. Combined ³He-Based in vivo Lung Morphometry and CT Data Allows for Unique Evaluation of Lung Parenchymal and Non-Parenchymal Tissue

In vivo lung morphometry technique provides information on geometrical parameters of lung acinar airways and alveoli that comprise lung parenchymal tissue (PT) participating in gas exchange. The rest of the lung tissue constitutes the so-called non-parenchymal tissue (NPT). This classification was proposed by Weibel (16). Herein we show that combining data obtained from in vivo lung morphometry with data obtained from quantitative CT, we can separately measure these two tissues – PT and NPT.

Using CT data, the specific volume of gas in lungs V_g can be related to HU (9,134) as follows:

$$V_g=\frac{1}{{\rho }_0}\cdot \frac{1000}{HU+1000}-\frac{1}{{\rho }_{t0}};{\rho }_0=1\mathrm{g}∕\mathrm{ml};{\rho }_{t0}=1.065\mathrm{g}∕\mathrm{ml}$$ [10]

In each voxel we define a volume of gas V_g, an overall volume of the tissue V_T, the volumes of PT and NPT, V_PT and V_NPT, respectively and the volume fractions of these two types of lung tissues, ζ_PT = V_PT / (V_T + V_g) and ζ_NPT = V_NPT / (V_T + V_g). Assuming all gas in the lungs is located in alveolar-covered acinar airways characterized by the surface S and separated from one another by the wall of the mean thickness d_w, the volume V_PT can be written as V_PT = S·d_w / 2. Hence:

$$\begin{array}{cc}\hfill {\zeta }_{PT}=& \left[1-\frac{{\rho }_0}{{\rho }_{T0}}\cdot \frac{(HU+1000)}{1000}\right]\cdot (S∕V)\cdot \frac{d_w}{2}\hfill \\ \hfill {\zeta }_{NPT}=& \frac{{\rho }_0}{{\rho }_{T0}}\cdot \frac{(HU+1000)}{1000}-\left[1-\frac{{\rho }_0}{{\rho }_{T0}}\cdot \frac{(HU+1000)}{1000}\right]\cdot (S∕V)\cdot \frac{d_w}{2}\hfill \end{array}$$ [11]

The surface-to-volume ratio (S / V) can be obtained from our in vivo lung morphometry technique (2) using Eqs. [4]. The thickness of alveolar walls is approximately d_w =10μm (135).

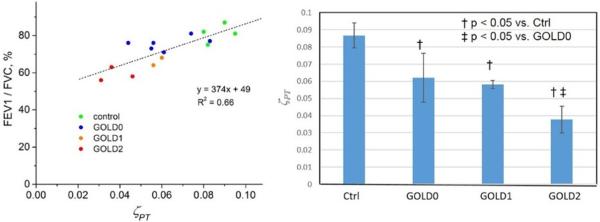
Results in Figure 19 show significant correlation between pulmonary characteristic FEV₁/FVC and parenchymal tissue density. Bar graph in this figure also shows statistically significant differences between groups based on their mean ζ_PT values. Hence, using combined data from ³He MRI and CT, we can estimate the lung parenchymal and non-parenchymal tissue that cannot be obtained by using these modalities alone.

Figure 19.

Example of data obtained from 4 healthy control subjects, 6 former smokers without COPD (previously known as GOLD0), 2 GOLD1 and 3 GOLD2 subjects. Left plot shows association between FEV₁/FVC [%] and mean parenchyma tissue density ζ_PT. Bar graph shows statistically significant differences between groups based on their mean ζ_PT values.

9. Combined ³He-based in vivo Lung Morphometry and Measurements of ³He Gas T2* Transverse Relaxation Properties

Important additional information on lung microstructure and functioning can be extracted by combining in vivo lung morphometry technique with measurements of transverse T2* relaxation properties of hyperpolarized gas in lung airspaces (61) which depend on tissue-specific mesoscopic magnetic field inhomogeneities induced by the susceptibility differences between lung tissue (alveolar septa, blood vessels) and lung airspaces. Such measurements are based on a gradient recalled echo GRE) experiment with multiple gradient echoes.

As demonstrated in (61), the MR signal dependence on gradient echo time TE can be presented in the form

$$S\left(TE\right)=S_0\cdot \exp (-R{2}^{\ast }\cdot TE)\cdot \exp \left[-\frac{1}{2}{(\delta \omega \cdot t_A)}^2\cdot \Psi (TE∕t_A)\right]\cdot F\left(TE\right)$$ [12]

Here R2* describes the signal decay due to the inhomogeneous magnetic fields created by the presence of mid-size (larger than capillary) blood vessels (136), Ψ is a function describing the signal decay due to the inhomogeneous magnetic fields created by the presence of the acinar airways (61), δω represents a dispersion of the Larmor frequency distribution created by the presence of acinar airways (61), and F(TE) describes the signal decay due to the macroscopic field inhomogeneities (background gradients) (137,138). The function F is calculated based on the GRE signal phase using voxel spread function approach (138). Phenomenological expression for the function Ψ was derived in (61), which depends on the dimensionless time TE / t_A with t_A being a characteristic diffusion time required for an atom to diffuse over an average length of acinar airways L_A, t_A = L²_A / 2D_L0, and the longitudinal diffusivity D_L0 is given in Eq. [18]. The theory of R2* relaxation due to the presence of mesoscopic field inhomogeneities created by blood vessel network was developed in (136):

$$R{2}^{\ast }=4\pi ∕3\cdot \gamma \cdot \Delta \chi \cdot B_0\cdot \zeta$$ [13]

where Δχ is the difference between susceptibilities of blood vessels and gas in lung airspaces, ζ is the mid-size blood vessel volume fraction, γ is the hyperpolarized gas nuclei gyromagnetic ratio, and B₀ is the strength of the external magnetic field.

The model given in Eq. [12] contains three parameters: the relaxation rate constant R2*, the frequency dispersion δω , and the characteristic diffusion time t_A. These parameters make it possible to estimate important morphological parameters of the lungs: the blood vessel volume fraction ζ, the average length of acinar airways L_A, and the specific volume of gas V_g (the volume of gas in the lungs per gram of tissue), which is often used to characterize lung tissue,

$$V_g=\left(\frac{\Delta \chi \cdot \gamma B_0}{3\sqrt{5}\cdot \delta \omega }-1\right)∕{\rho }_t$$ [14]

where ρ_t =1.065 g/ml is the lung tissue density. This expression allows calculation the specific gas volume that is usually obtained from CT measurements (9,134) – see also discussion above.

An example of the data obtained by combining GRE measurements with in vivo lung morphometry is shown in Figure 20.

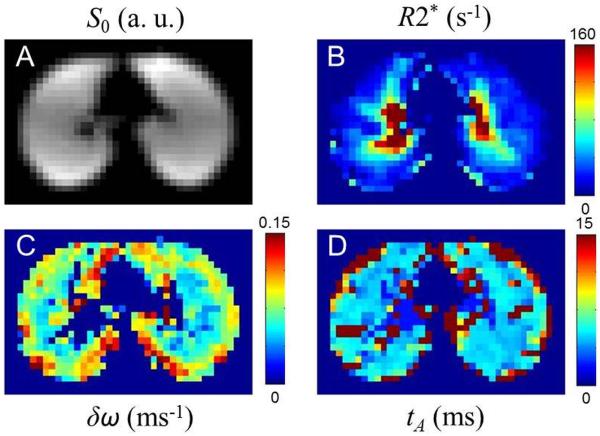
Figure 20.

Signal amplitude, S₀ (A), and maps of the three model parameters –the relaxation rate constant R2* (B), the frequency dispersion δω (C), and the characteristic diffusion time t_A (D).

The map of the relaxation rate constant R2* is substantially inhomogeneous: in the central part of the lung this parameter is high whereas at the periphery it becomes very small. High values of R2* in the central part correspond to the regions of high concentration of non-capillary blood vessels. The parameter δω reveals rather homogeneous behavior except for lung periphery. The map of the characteristic time t_A is also rather homogeneous. The values of the model parameters averaged over 8 healthy volunteers are as follows: R2* = 31±6 s⁻¹, δω = 73±6 s⁻¹, t_A = 5.6±0.5 ms. The corresponding morphometric parameters found by combining the model parameters with the results of in vivo lung morphometry technique, ζ = 3.3±0.6%, L_A = 749±105 μm, V_g = 4.4±0.4 ml/g, are in good agreement with known experimental data (9,17,139).

10. Measurements of Anisotropic Diffusion of Hyperpolarized ¹²⁹Xe Gas in Acinar Airways

To develop the lung morphometry technique with hyperpolarized ¹²⁹Xe, we need to take into account differences in magnetic and diffusion properties of ¹²⁹Xe as compared to ³He gas. With proper selection of ¹²⁹Xe diffusion time, Eqs.[7]-[8] can still be used, but Eqs. [18]-[19] should be modified due to the differences in the gyromagnetic ratios and in the free diffusion coefficients (see Table 1). In (65), phenomenological expressions similar to Eqs. [18]-[19] were derived for ¹²⁹Xe gas both for humans and small animals.

For the geometrical model in Figure 3, the dimensionless longitudinal and transverse apparent diffusivities are functions of two independent geometrical dimensionless parameters r / R and R / L₁ and the product bD₀:

$$\frac{D_L}{D_0}=F_L\left(b{D}_0,\frac{r}{R},\frac{R}{L_1}\right),\frac{D_T}{D_0}=F_T\left(b{D}_0,\frac{r}{R},\frac{R}{L_1}\right)$$ [15]

Importantly, D_L and D_T determined from the MR experiment, depend on both lung microstructure and the details of the Stejskal-Tanner pulse sequence (diffusion attenuated gradients strength and duration (4). Generally speaking, one can modify the gradient pulse sequence parameters (diffusion time Δ, gradient amplitude G_m) in such a way that the dimensionless combinations R / L₁ and bD₀ would be the same as for ³He. This can be achieved with the following substitutions:

$${\Delta }^{\left(\mathrm{Xe}\right)}=\frac{D_0^{\left(\mathrm{He}\right)}}{D_0^{\left(\mathrm{Xe}\right)}}\cdot {\Delta }^{\left(\mathrm{He}\right)},G_m^{\left(\mathrm{X}e\right)}=\frac{D_0^{\left(\mathrm{Xe}\right)}}{D_0^{\left(\mathrm{He}\right)}}\cdot \frac{{\gamma }^{\left(\mathrm{He}\right)}}{{\gamma }^{\left(\mathrm{Xe}\right)}}\cdot G_m^{\left(\mathrm{H}e\right)}$$ [16]

In this case, all the expressions derived for 3He, in Eqs. [18]-[19], can be directly applied to experiments with 129Xe. This choice, however, would lead to an increase in the diffusion time Δ by a factor of 6.3 that would substantially increase the imaging time. On a positive side, the required diffusion gradient strength would be reduced by a factor of 0.44. Hence, for the 129Xe experiment we can select a smaller diffusion time by simultaneously adjusting the diffusion gradient strength. For state-of-the-art human scanners allowing diffusion gradient strengths up to 30-40 mT/m, as shown in (65), the smaller value of the diffusion time Δ = 5 ms can be selected for human lung imaging, while for small animal scanners, allowing ten-fold stronger gradients, this time is about 1 ms. For both cases, a new set of equations relating the geometrical parameters of acinar airways to measured anisotropic ADCs should be derived.

It should also be noted that the gas concentration may vary across the lung which could lead to bias in estimating both standard ADC values and lung morphometric parameters. This effect could be especially pronounced for ¹²⁹Xe gas due to its higher atomic weight and viscosity (as compared to ³He). That is why there is one more important issue related to the value of the “free” diffusion coefficient D₀, which significantly depends on gas concentration and varies from 0.06 cm² /s for ¹²⁹Xe self-diffusion to 0.14 cm² /s for ¹²⁹Xe diluted is air or N₂ (see Table 1). In (65), the expressions similar to Eqs. [18]-[19] were derived for diluted ¹²⁹Xe gas with D₀ = 0.14 cm² /s. However, for a typical gas mixture in human lungs (1 L of ¹²⁹Xe + 3 L of air), the ¹²⁹Xe diffusion coefficient D₀ is about 0.1 cm² /s. The corresponding phenomenological expressions valid for D₀ = 0.1cm² /s (~30% of ¹²⁹Xe in air or N₂), R = 280–400 μm, and Δ = 4–6 ms were derived in (140) and are presented in the Appendix, Eqs. [20]-[22].

The first ¹²⁹Xe applications of in vivo lung morphometry technique have been demonstrated by Ruppert et al in humans (92) and Boudreau et al in rats (93). Applications to study subjects with COPD and healthy volunteers were implemented by Ouriadov et al (141). Fitting the mathematical model in Eqs. [20]-[22] to experimental data revealed significant morphological differences between the COPD subjects and healthy volunteers, specifically decreases in h (68 ± 36 μm vs 95 ± 70 μm, respectively, P = 0.019) and increase in L_m (352 ± 57 μm vs 253± 37 μm, respectively, P = 0.002). Importantly, the values of morphological parameters obtained with ¹²⁹Xe are consistent with those obtained with ³He MRI in similar subjects.

Usual procedure of applying in vivo lung morphometry technique assumes that the D₀ coefficient is known as described above based on a typical concentration of hyperpolarized gas. An interesting extension of the in vivo lung morphometry technique was proposed by Ouriadov et al (142), where D₀ was considered as an additional fitting parameter. As was found in (142), D₀ demonstrated significantly (P<0.035) increase in smokers with COPD (0.14 ± 0.03 cm² /s) as compared to never-smokers (0.12 ± 0.02 cm² /s).

¹²⁹Xe gas concentration used in experiments with small animals is usually higher than for humans. Assuming D₀ = 0.14 cm² /s, it is easy to verify that for R =100 μm, Δ =1.3 ms, the characteristic ratio R / L₁ = 0.52, that is very close to the ratio for ³He gas R / L₁ = 0.53 in normal human lungs with the parameters D₀ = 0.88 cm² /s, R = 300 μm and Δ =1.8 ms. That is why the phenomenological expressions relating D_L and D_T with the geometrical parameters R and r are the same as in Eqs. [18]-[19]. These equations was used to investigate early stage radiation induced lung injury in a rat model (143). The irradiated rats revealed significant difference (P<0.02) in the lung morphometric parameters R, r, and L_m: (74±17 μm, 43±12 μm, 54±17 μm, respectively) in the irradiated rats. vs 100±12 μm, 67±10 μm, 79 ±12 μm, respectively) in the control rats.

11. ADC Measurements in Healthy and Diseased Lungs

Most of our review is devoted to discussion of quantitative measurements of lung microstructural parameters that are based on in vivo lung morphometry technique. At the same time, numerous measurements have also been performed based on diffusion MRI with only two b-values allowing only measurements of ADC per Eq. [3]. Since ADC measurements are usually done with only two b-values, they allow obtaining ADC maps from a substantial part of the lungs in a single breath-hold. Already initial publications (3,144-146) demonstrated that ADC of hyperpolarized ³He gas in the lungs dramatically increases in emphysema (compared to normal lungs), suggesting a large potential as a diagnostic tool for clinical applications.

In order to properly design the diffusion experiment we need first to evaluate diffusion times necessary for gas atoms to explore distances characteristic for acinar airways and alveoli. For a random walk Brownian motion, in time interval Δ (diffusion time), in the absence of restricting walls or barriers the gas molecules would move a root mean-square distance L₁ = (2D₀Δ)^1/2 along any axis. The free diffusion coefficient D₀ for diluted ³He in air at 37°C is D₀ = 0.88 cm² /s (Table 1). Hence ³He gas atoms can wander distances on the order of 1 mm in times as short as 1 ms. This distance is comparable with characteristic sizes of acinar airways in a human lung – a typical acinar airway has a diameter of about 0.7 mm and a length of 1mm (17). For reasons described above, most ADC measurements so far have been done in the millisecond diffusion time frame (see, e.g. (3,6,89,144-174)).

Diffusion MRI with hyperpolarized gases has also been used in studying asthma (175), (176), (177), bronchiolitis obliterans in post-transplantation lungs (178), pulmonary fibrosis (178), (179), and cancer (180), (181), (182), (183).

Although ADC measurements are rather simple, even in healthy human lungs ADC exhibits rather broad variability, with different studies (90,145,149,159,161-163,184) reporting results between 0.15 cm²/s and 0.25 cm²/s for ³He ADC. Quite a few authors have also reported measurements of ¹²⁹Xe-based ADC in healthy and emphysematous lungs (43,93,166,185-188). Kirby et al (188) demonstrated a significant correlation between ³He ADC and ¹²⁹Xe ADC as well as between ADCs and CT measurements. In healthy lungs, ³He ADC and ¹²⁹Xe ADC were found to be ~ 0.20 cm²/s and ~0.055 cm²/s, respectively; in lungs with COPD, the corresponding values are ~0.55-0.6 cm²/s and 0.07-0.09 cm²/s. In (187), the mean ¹²⁹Xe ADC in healthy volunteers was reported ~0.04 cm²/s.

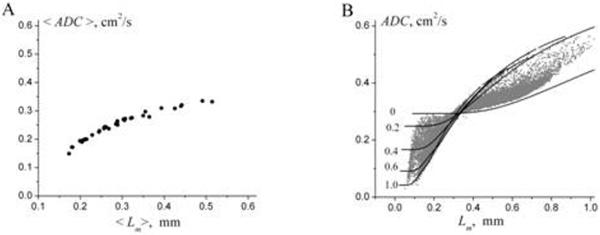
The discrepancies between different ADC studies are not unexpected. As we already discussed above, this is due to the fact that ADC depends not only on lung microstructure but on pulse sequence parameters (diffusion time Δ, b-value). Besides, even for fixed pulse sequence parameters, there is no one-to-one correspondence between ADC and lung morphometric parameters. To demonstrate this, in Figure 21a, we accumulated the results of the study (6) for 30 subjects and plotted ADC vs. Lm (calculated on a pixel-by-pixel basis) (gray symbols). The lines represent the dependence of ADC as a function of mean linear intercept Lm, theoretically calculated at fixed values of the ratio h/R (given by numbers near the lines) by using Eqs. [18]-[19] and

$$ADC=\frac{1}{3}{D}_{L0}+\frac{2}{3}{D}_{T0}$$ [17]

Figure 21.

ADC vs Lm found in for 30 subjects from study (6). (A) The average (over each subject) values of the parameters ADC and Lm. (B) ADC and Lm calculated on a pixel-by-pixel basis (grey symbols). The lines represent the dependence of ADC as a function of Lm, theoretically calculated at fixed values of the ratio h/R (given by numbers near the lines). Importantly, each value of Lm can be associated with numerous values of ADC, and vice versa.

As we see, each value of Lm can be associated with numerous values of ADC, and vice versa. It means that the correlation between these two parameters is very limited. That is why ADC, though quite useful, is not sufficiently informative parameter for characterizing lung microstructure.

While most ADC measurements cited above were conducted using short diffusion times (a few ms) exploring lung structure at the acinar level, measurements of the ³He diffusion coefficient at longer diffusion times (seconds) (75,176,189-194) allow exploring the “connectivity” of acinar airways and alveoli thus providing information on airway and alveolar wall integrity (i.e., holes through the walls) and collateral ventilation pathways (75,192). Mugler et al (194) and Wang et al (176) reported measurements for diffusion times ranging from milliseconds to seconds. In healthy subjects, they found that the apparent diffusion coefficient decreased by about 10-fold, from approximately 0.2 to 0.02 cm²/second, as the diffusion time increased from approximately 1 millisecond to 1 second. Such a decrease is similar to result by Woods et al (190).

CONCLUDING REMARKS

Over decades, quantification of lung microstructure has relied on evaluation of histological sections. These time-consuming invasive studies are not practical for clinical applications and provide information only on a very limited number of lung specimens. The introduction of hyperpolarized gases (³He and ¹²⁹Xe) and their use in lung diffusion MRI has crucially changed the situation. Starting from simple ADC measurements and then moving to more advanced approaches (i.e. in vivo lung morphometry technique) made it possible providing unique 3D tomographic information on lung microstructure from a short (less than 15 seconds) MRI scan. The latter technique has the ability to measure the same physiological parameters that were traditionally obtained by means of “standard” stereology (mean linear intercept,Lm, surface-to-volume ratio S/V, number of alveoli per unit volume N_a), and became a gold standard for quantifying lung microstructure in health and disease. Importantly, this new approach also provides measurements of advanced parameters introduced by Weibel to characterize lung microstructure - radii of alveolar sacs and ducts, as well as the depth of their alveolar sleeves. Combining with CT measurements and/or gradient echo lung MRI, additional lung parameters can be obtained: blood vessel volume fraction, specific gas volume, the length of acinar airways, and unique evaluation of lung parenchymal and non-parenchymal tissue.

By making use of the in vivo lung morphometry technique in healthy lungs reveals previously unknown changes in lung microstructure throughout the adult life span, made it possible to differentiate normal aging lungs and accelerated aging lungs with emphysema, allowed detecting early emphysematous changes in lung microstructure in current and former smokers, and changes in the lung microstructure after pneumonectomy.

These safe and sensitive diffusion measurements improve our understanding of lung structure and functioning in health and disease, providing a platform for monitoring the efficacy of therapeutic interventions in clinical trials. In vivo lung morphometry with ³He gas is a unique tool for studying specific lung diseases (e.g., emphysema, asthma, bronchopulmonary dysplasia developing in premature newborns, alpha-1 antitrypsin deficiency, etc.).

It should be mentioned that, though ³He gas MRI can be effectively used for research, its clinical application are limited due to a shortage of the gas and its increasing cost (195). Although recapture/reuse systems are being implemented (196) and will help to extend the gas supply. An alternative “hyperpolarizable” gas, ¹²⁹Xe, is cheaper and more readily available suggesting that it can become the gas of choice for these new techniques. Theoretical background for in vivo lung morphometry with hyperpolarized ¹²⁹Xe has already been developed (65) and preliminary data (92,93,141-143) demonstrate the potential of this approach (see detailed discussion in the Section 10).

Appendix

The relationship between the longitudinal and transverse diffusivities D_L and D_T and geometrical parameters of acinar airways.

• a)
  ³He gas in human lungs (2); valid for D₀ ≈ 0.88 cm² /s (diluted ³He in air or N₂), R = 280–400 μm, Δ = 1.5–2 ms

  $$\begin{array}{cc}\hfill & \frac{D_{L0}}{D_0}=\exp \left[-2.89\cdot {\left(h∕R\right)}^{1.78}\right]\hfill \\ \hfill & {\beta }_L=35.6\cdot {\left(R∕L_1\right)}^{1.5}\cdot \exp \left[-4∕\sqrt{h∕R}\right]\hfill \end{array}$$ [18]

  $$\begin{array}{cc}\hfill & \frac{D_{T0}}{D_0}=\exp \left[-0.73\cdot {\left(L_2∕R\right)}^{1.4}\right]\cdot \left\{1+\exp \left(-A\cdot {(h∕R)}^2\right)\cdot u(h∕R)\right\}\hfill \\ \hfill & u(h,R)=\exp \left(-5\cdot {(h∕R)}^2\right)+5\cdot {(h∕R)}^2-1\hfill \\ \hfill & A=1.3+0.25\cdot \exp \left[14\cdot {\left(R∕L_2\right)}^2\right]\hfill \end{array}$$ [19]

  Here L₁ = (2D₀Δ)^1/2 and L₂ = (4D₀Δ)^1/2 are the characteristic free-diffusion lengths for one- and two-dimensional diffusion, respectively. In the physiological range (h / R < 0.6), parameter β_T remains practically constant at approximately 0.06.
• b)
  ¹²⁹Xe gas in human lungs (140); valid for D₀ ≈ 0.1cm² /s (~30% of ¹²⁹Xe in air or N₂), R = 280–400 μm, Δ = 1.5–2 ms

  $$\begin{array}{cc}\hfill & D_{L0}∕D_0=\exp \left[-2.81\cdot {(h∕R)}^{1.76}\right]\hfill \\ \hfill & {\beta }_L=16.5\cdot {(R∕L_1)}^{3∕2}\cdot \exp \left[-3.51∕\sqrt{h∕R}\right]\hfill \end{array}$$ [20]

  $$\begin{array}{cc}\hfill & D_{T0}=D_0\cdot \exp \left[-0.73\cdot {(L_2∕R)}^{1.51}\right]\cdot [1+u(h,R)]\hfill \\ \hfill & u(h,R)=c_1\left(R\right)\cdot (h∕R)+c_2\left(R\right)\cdot {(h∕R)}^2\hfill \\ \hfill & c_1\left(R\right)=0.19+0.32\cdot (R∕L_2)-0.68\cdot {(R∕L_2)}^2\hfill \\ \hfill & c_2\left(R\right)=2.08-6.82\cdot (R∕L_2)+4.14\cdot {(R∕L_2)}^2\hfill \end{array}$$ [21]

  $$\begin{array}{cc}\hfill & {\beta }_T=c_0^{\prime }\left(R\right)+c_1^{\prime }\left(R\right)\cdot r∕R+c_2^{\prime }\left(R\right)\cdot {(r∕R)}^2\hfill \\ \hfill & c_0^{\prime }\left(R\right)=1.69-4.93\cdot (R∕L_2)+2.75\cdot {(R∕L_2)}^2\hfill \\ \hfill & c_1^{\prime }\left(R\right)=-3.19+10.32\cdot (R∕L_2)-6.24\cdot {(R∕L_2)}^2\hfill \\ \hfill & c_2^{\prime }\left(R\right)=1.62-5.40\cdot (R∕L_2)+3.32\cdot {(R∕L_2)}^2\hfill \end{array}$$ [22]
• c)
  ³He gas in mice lungs (86); valid for: D₀ ≈ 1.7 cm² /s (pure ³He at room temperature), R = 60–140 μm, Δ = 0.4–0.5 ms

  $$\begin{array}{cc}\hfill & D_{L0}=D_0\cdot \exp \left[-2.99\cdot {(h∕R)}^{1.88}\right]\hfill \\ \hfill & {\beta }_L=113.5\cdot {(R∕L_1)}^{1.5}\cdot \exp \left[-5.11∕\sqrt{h∕R}\right]\hfill \end{array}$$ [23]

  $$\begin{array}{cc}\hfill & D_{T0}=D_0\cdot F\left(R\right)\cdot [1+u(h,R)]\hfill \\ \hfill & F\left(R\right)=\frac{7}{16}\cdot \exp \left[\left((4-3.63\cdot {(R∕L_2)}^{0.6}\right)\cdot \ln (R∕L_2)\right]\hfill \\ \hfill & u(h,R)={(h∕R)}^{1.75}\cdot \exp (A\cdot h∕R)\hfill \\ \hfill & A=1.1+3.14\cdot R∕L_2-18.39\cdot {(R∕L_2)}^2\hfill \\ \hfill & {\beta }_T=0\hfill \end{array}$$ [24]