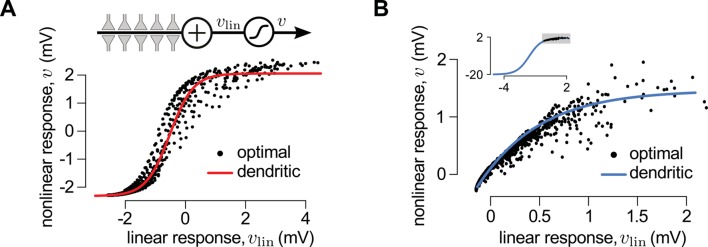
Figure 3. A canonical model of dendritic integration approximates the optimal response.

(A) The optimal response (black) and the response of a canonical model of a dendritic branch, $v$ (inset), with a sigmoidal nonlinearity (red, Equation 25) as functions of the linearly integrated input, $v_{\mathrm{lin}}$ (inset, Equation 24), when the presynaptic population exhibits synchronized switches between a quiescent and an active state, as in Figure 2D. Black dots show optimal vs. linear postsynaptic response sampled at regular $2.5$ ms intervals during a $3$ s-long simulation of the presynaptic spike trains. (B) Optimal response (black) approximated by the saturating part of the sigmoidal nonlinearity (blue) when the presynaptic population is fully characterized by second-order correlations, as in Figure 2A. Inset shows the same data on a larger scale to reveal the sigmoidal nature of the underlying nonlinearity (gray box indicates area shown in the main plot).

DOI: http://dx.doi.org/10.7554/eLife.10056.012

Figure 3—figure supplement 1. Reducing the optimal response with second order correlations to a canonical model of dendritic integration.

(A–C) Comparing the full (Equations 20–23) and the reduced model Equations A99-A100) of the optimal response. The estimates of the mean presynaptic membrane potential by the full model (A, grey) and the reduced model (A, black) are nearly identical. The error of the reduced model (quantified as the mean squared difference between the two models normalized by the variance of the full model) decreases monotonically with increasing correlations in the presynaptic population (B) and remains bounded as the number of neurons increases (C). (D) Steady state posterior variance, ${\overline{\sigma }}_{\mathrm{\infty }}^2$, as a function of the posterior mean, $\overline{\mu }$, in the reduced model (Equation A100). (E) Comparing the linear-nonlinear model and the optimal response. Black dots: the optimal response against the output of the linear model, $v_{\mathrm{lin}}$ (Equation 24). Blue line: sigmoidal nonlinearity operating in the linear-nonlinear model at the arrival of spikes, $h\left(v_{\mathrm{lin}}\right)$ (Equation A103). Orange line: the result of numerically fitting a sigmoidal nonlinearity in the canonical model (Equation 25) to the optimal response. Parameters were $N=10$, $g=2$ Hz (A–C), or $N=1$, $g=20$ Hz (D–E), and $\beta =2$ mV${}^{-1}$, $\tau =20$ ms, ${\mathrm{\Sigma }}_{ii}=1$ mV${}^2$ (A–E), and $\rho =0.5$ (A) or as indicated on the x-axis (B) or in the legend (C). For details, see Appendix B.

DOI: http://dx.doi.org/10.7554/eLife.10056.013

Figure 3—figure supplement 2. Adaptation without parameter change.

(A) We simulated a presynaptic population with two different global activity states, a synchronized and a desynchronized state and first determined the optimal response in the two states separately (black). Next, we trained a linear (grey) and a nonlinear (red) dendrite to approximate the optimal response in both the synchronized and the desynchronized state (grey). (B) Green and black dots indicate the optimal response as a function of the best linear response respectively during the desynchronized and synchronized states. The same single dendritic nonlinearity (red line) can efficiently approximate the optimal response in both states simply because each state uses a different part of the input range of this nonlinearity: during the synchronized state the expansive supralinearity of the upstroke is being predominantly used, while during the desynchronized state the saturating sublinear-linear regime is dominating the response. (C) The error of the dendritic response is slightly larger than that of the optimal response but still substantially smaller than the error of the linear response. Parameters of the synchronized state were ${\mathrm{\Omega }}_{-}=10$ Hz, ${\mathrm{\Omega }}_{+}=0.7$ Hz, $\overline{u}=2.3$ mV, $\tau =20$ ms, ${\mathrm{\Sigma }}_{ii}=1$ mV${}^2$, ${\mathrm{\Sigma }}_{ij}=0.5$ mV${}^2$, $g=5.3$ Hz, $\beta =0.5$ mV${}^{-1}$, ${\tau }_{\text{refr}}=1$ ms and ${\mathrm{p}}_{\mathrm{rel}}=1$ and the desynchronized state was identical to a persistent active phase of the synchronized state.

DOI: http://dx.doi.org/10.7554/eLife.10056.014