Fig. S5.

We developed a hybrid model that has parameters for separate updates following hits (α_hit) and misses (α_miss), as well as the probability of hits (α_prob). This hybrid model captures the ability of the gating model to discount misses by having a low value of α_miss, effectively pausing learning when a motor error is present. Additionally, the model tracks the probability of motor success with the α_prob parameter,

$$\begin{array}{l}{\widehat{p}}_{t+1}\left(x\right)={\widehat{p}}_t\left(x\right)+{\alpha }_{prob}{\delta }_{prob,t}\\ E_{t+1}\left(x|hit\right)=E_t\left(x\right)+{\alpha }_{hit}{\delta }_t\\ E_{t+1}\left(x|miss\right)=E_t\left(x\right)+{\alpha }_{miss}{\delta }_t\\ V_{t+1}\left(x\right)={\widehat{p}}_{t+1}\left(x\right)+E_{t+1}\left(x\right).\end{array}$$

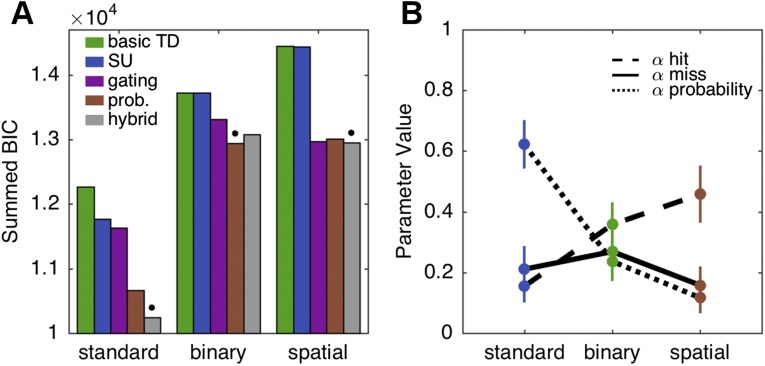
We fit the hybrid model to the data in experiment 1 using the method specified in Modeling Analysis. The model provided a better fit than the gating and probability models (after correcting for the additional free parameter) in both the Spatial and Keyboard conditions but actually performed worse than the probability model in the Binary condition (A). Although the hybrid model should be able to do at least as well as the other two models (given that it contains the parameters of the other models), we used a fitting procedure that optimizes the model fit for all conditions at once to obtain a single value of the temperature parameter, β. With this procedure, it is not mandatory that the hybrid model outperform the other two models in every condition. The probability model provided a significantly better fit in the Standard (BIC difference from next best model, −414.2) and Spatial conditions (−20.70), but not the Binary condition (+139.60). In terms of mean parameter values (B) for the Spatial group, the hybrid model indicates that both the probability representation ($\widehat{p}$) after all trials, and the value representation (E_t) after a miss trial, are very weakly updated. These results further suggest that the gating mechanism may be significantly present in the Spatial case (low α_miss) whereas the probability/competence mechanism makes a modest contribution (low α_prob), a result that is consistent with that observed from the parameter estimates from the separated gating and probability models (Fig. 3 B and C). On the other hand, the Standard condition shows a relatively high value of α_prob, suggesting that the probability mechanism is driving choice behavior in this condition. Again, the Binary condition lies in the middle.