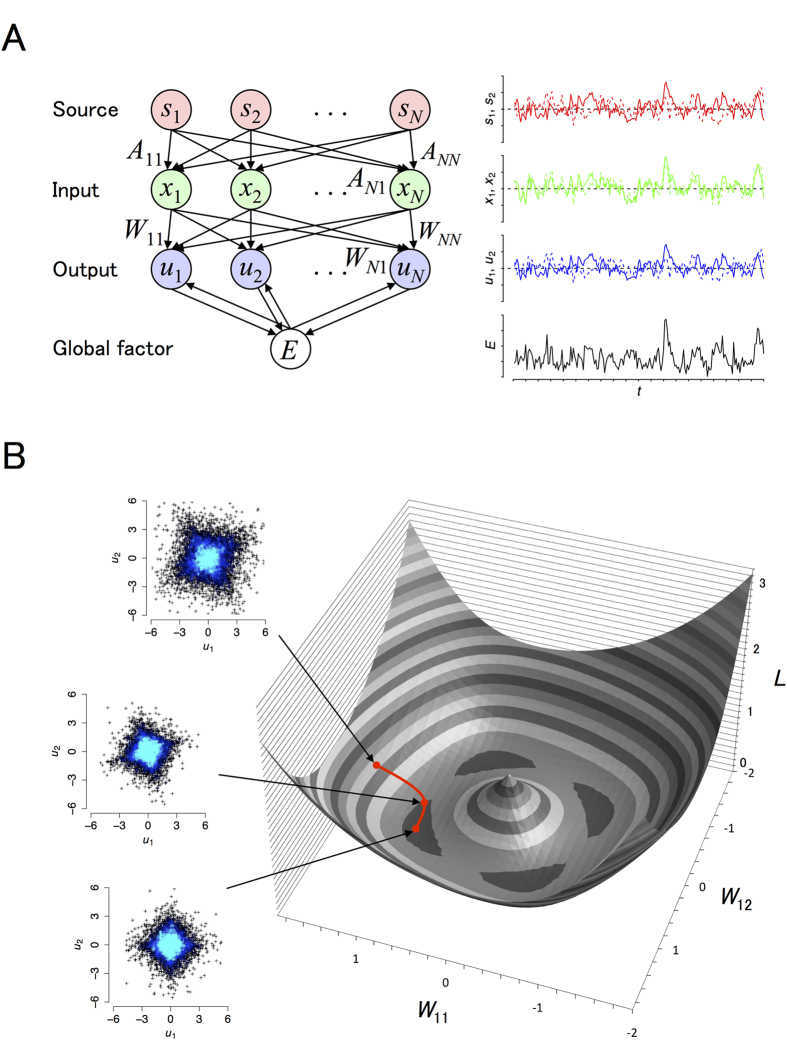
Figure 1. Schematic image of the model setup and results of the proposed learning rule.

(A) Left: Schematic image of the model. The input x to the neural network is a linear mixture of independent sources s, i.e., x = As, where A is a mixing matrix. The neural network linearly sums the input and produces the output u = Wx, where W is a synaptic strength matrix. The goal is to learn the W ∝ A⁻¹ (or its row permutations and signflips) for which the outputs become independent. To this end, a global signal E is computed based on the outputs of individual neurons and gate activity-dependent changes in W during learning. Right: Time traces of s, x, u, and E. (B) A dynamic trajectory of the synaptic strength matrix while the network learns to separate independent sources. The learning rule is formulated as a gradient descent algorithm of a cost function L, whose landscape is depicted as a function of synaptic strength parameters (W₁₁, W₁₂). Note that in order to graphically illustrate the results in this three-dimensional plot, we used a two-dimensional rotation matrix with angle 6/π as the mixing matrix A and restricted W as a rotation and scaling matrix (W₁₁, W₁₂; −W₁₂, W₁₁). The red trajectory displays how the gradient descent algorithm reduces the cost function L by adjusting (W₁₁, W₁₂). The three inset panels display the distributions of the network output (u₁, u₂) during the course of the learning. Each point represents sampled outputs and the brightness of the blue color represents probability density. Top: The outputs are not independent at the initial condition (W₁₁, W₁₂) = (1.5, 0). Middle: The distribution of the outputs is rotated during learning. Bottom: The network outputs become independent at the final state (W₁₁, W₁₂) = (cos 6/π, sin 6/π). The two sources are drawn independently from the same Laplace distribution (see Methods). Note that a MATLAB source code of the EGHR is appended as Supplementary Source Code 1.