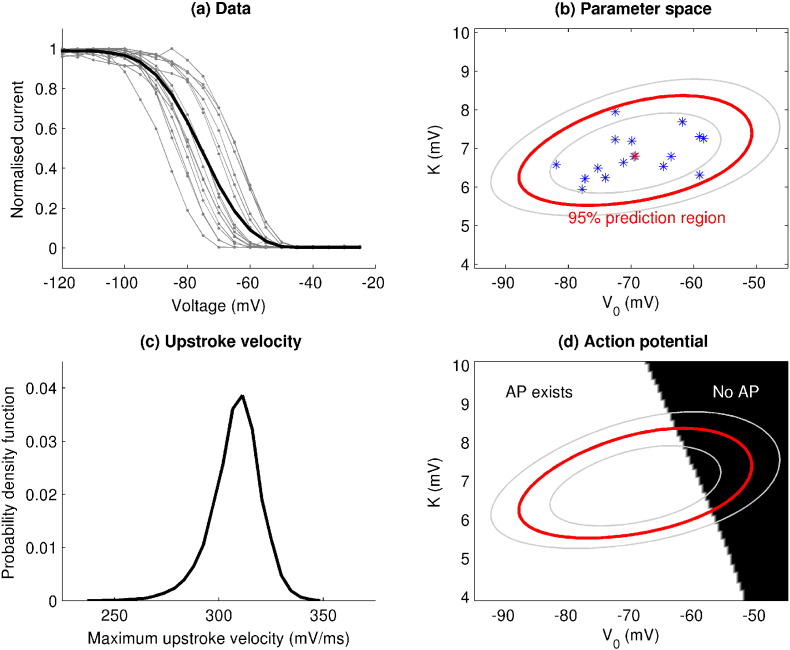
Fig. 1.
Pipeline of the UQ process, applied to variability in steady-state INa inactivation (image adapted from [38]). Using experimental data on steady-state INa inactivation from canine myocytes (sub-figure (a), individual cells in grey, averaged data in black, note how the slope of the average does not match the slope of any individual), uncertainty due to population variability was characterised by fitting a two-parameter sigmoidal curve using the statistical method nonlinear mixed effects to estimate the variability in the two parameters. Sub-figure (b) illustrates the mean (red star) and variability (red ellipse: 95%; grey ellipses: 80% and 99%) of the two parameters (blue stars represent parameters for individual cells). The mean corresponds to an ‘average’ cell, not the averaged data. This inactivation sub-model was then embedded in the Fox et al.[12] canine AP model, and the parameter uncertainty was propagated through the model to obtain a probability distribution for upstroke velocity (subfigure (c)). However, the model did not repolarise for a region of parameter space that overlapped with the population variability (subfigure (d)).