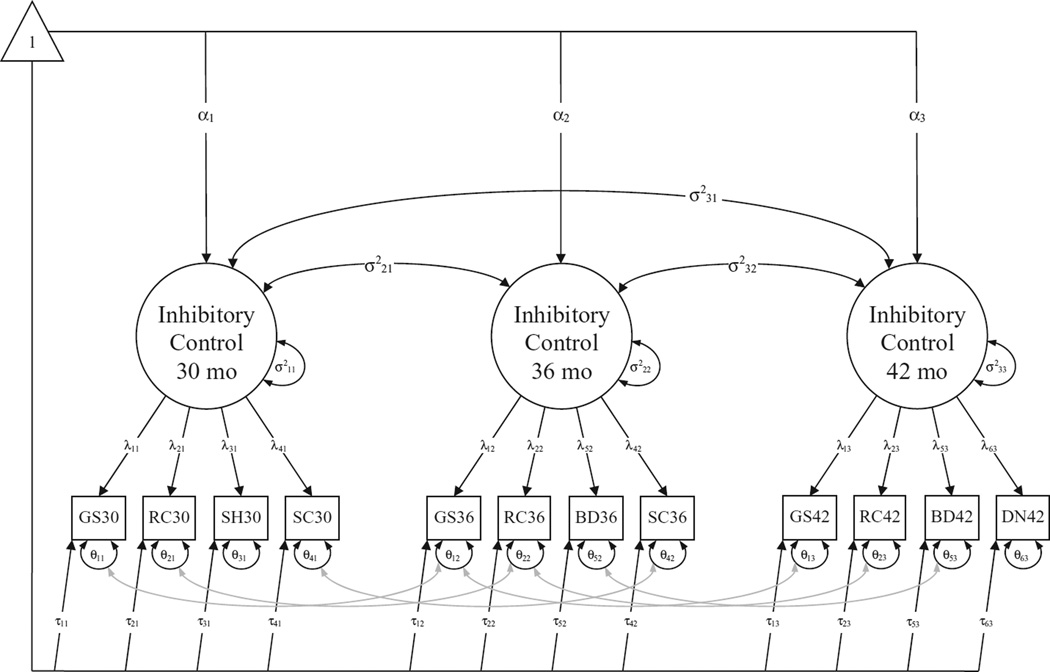
Fig. 5.

Example baseline longitudinal CFA model of inhibitory control adapted from Widaman et al. (2010) for use with changing measures over time. In the example model, the four measures at each time point (rectangles) serve as manifest variables (indicators) of the latent variable reflecting inhibitory control at each time point (ovals). The example baseline model is an abridged CFA with only three time points for pictorial simplicity. A full test of longitudinal factorial invariance would incorporate all nine measurement occasions from Table 6. See Table 5 for a list of the constraints added to the baseline model to test longitudinal factorial invariance. Constraints are only made within measure. For factor loadings (λ), residual variances (θ), and intercepts (τ), the first numerical digit refers to the measure (e.g., 2 from λ₂₃ = Grass/Snow) and the second digit refers to the occasion of measurement (e.g., 3 from λ₂₃ = Time 3: 42 months). For covariances (σ²), the first numerical digit refers to the occasion of measurement from one end of the arrow and the second digit refers to the occasion of measurement of the other arrow. The covariance of a variable with itself represents that variable’s variance. The triangle represents the estimation of means (intercepts), including the means of the latent factors (α) and the intercepts of the indicators (τ). “mo” = child’s age in months, BD = Bear/Dragon, DN = Day/Night, GS = Grass/Snow, RC = Reverse Categorization, SH = Shape Stroop, SC = Spatial Conflict.