Abstract
The voltage sensitivity of membrane proteins is reflected in the response of the voltage sensing domains (VSDs) to the changes in membrane potential. This response is implicated in the displacement of positively charged residues, associated with the conformational changes of VSDs. The displaced charges generate nonlinear (i.e., voltage-dependent) capacitance current called the gating current (and its corresponding gating charge), which is a key experimental quantity that characterizes voltage activation in VSMP. However, the relevant theoretical/computational approaches, aimed to correlate the structural information on VSMP to electrophysiological measurements, have been rather limited, posing a broad challenge in computer simulations of VSMP. Concomitant with the development of our coarse-graining (CG) model of voltage coupling, we apply our theoretical framework for the treatments of voltage effects in membrane proteins to modeling the VSMP activation, taking the VSDs (Ci-VSD) derived from the Ciona intestinalis voltage sensitive phosphatase (Ci-VSP) as a model system. Our CG model reproduces the observed gating charge of Ci-VSD activation in several different perspectives. In particular, a new closed-form expression of the gating charge is evaluated in both nonequilibrium and equilibrium ways, while considering the fluctuation–dissipation relation that connects a nonequilibrium measurement of the gating charge to an equilibrium measurement of charge fluctuations (i.e., the voltage-independent linear component of membrane capacitance). In turn, the expression uncovers a novel link that connects an equilibrium measurement of the voltage-independent linear capacitance to a nonequilibrium measurement of the voltage-dependent nonlinear capacitance (whose integral over voltage is equal to the gating charge). In addition, our CG model yields capacitor-like voltage dependent free energy parabolas, resulting in the free energy difference and the free energy barrier for the Ci-VSD activation at “zero” (depolarization) membrane potential. Significantly, the resultant voltage dependent energetics enables a direct evaluation of capacitance–voltage relationship (C–V curve) as well as charge–voltage relationship (Q–V curve) that is in a good agreement with the observed measurement of Ci-VSD voltage activation. Importantly, an extension of our kinetic/thermodynamic model of voltage dependent activation in VSMP allows for novel derivations of voltage-dependent rate constants, whose parameters are expressed by the intrinsic properties of VSMP. These novel closed-form expressions offer a physicochemical foundation for the semiempirical Eyring-type voltage dependent rate equations that have been the cornerstone for the phenomenological (kinetic) descriptions of gating and membrane currents in the mechanistic study of ion channels and transporters. Our extended theoretical framework developed in the present study has potential implications on the roles played by gating charge fluctuations for the spike generations in nerve cells within the framework of the Hodgkin–Huxley-type model.
Graphical Abstract
I. INTRODUCTION
The voltage activity of voltage sensitive membrane proteins (VSMP) is critical for many biological processes, including the generation and propagation of action potentials in nerve cells,1,2 a certain enzymatic reaction in reproductive cells,3 and proton extrusion in Phagocytes.4,5 The voltage sensitivity is reflected in the corresponding interaction of the voltage with the positively charged residues in the S4 helix of the voltage sensing domain (VSD) in VSMP. The displacements of positively charged residues in response to the changes in membrane potential generates the nonlinear capacitance current called gating current,6 recorded in a complete electric circuit. The corresponding gating charge is the experimentally measurable quantity that characterizes the voltage sensitivity in VSMP,7 which has provided a key information on the molecular action of VSD voltage activation.8
While several theoretical/computational approaches have been developed to quantify the gating charge,9–13 all of these approaches can be regarded as “indirect”, in that the calculations of the gating charge are based on the Hamiltonian (the membrane/protein system) described by the voltage (i.e., membrane potential) coupling to the gating-charge carrying residues, rather than directly measure the external charges that flow through electrolyte solutions, which is eventually recorded in an electric circuit. These approaches do not reflect a nonequilibrium nature of the gating charge since they are only applied to “equilibrium” situations. Nevertheless, these approaches have some success in estimating the gating charge in some of voltage gated ion channels13–15 while they have limited applicability to simulate the voltage dependency of VSMP activation, e.g., gating “current”,16 charge–voltage relationship,11 (Q–V curve) and capacitance–voltage relationship (C–V curve).
Our earlier study introduced a coarse-graining model (CG) of voltage coupling in membrane proteins that include the compete electrode, electrolyte, protein, and membrane systems.17 This model allowed us to evaluate the gating charge by directly measuring the external charges that flow through electrolyte solutions, considering the changes in the electrolyte distributions between the initial and the final configurations of amino acid analogues.18 The CG approach of ref 17 allowed us to explore the coupling to the external voltage by applying a nonequilibrium direct way of the type used in simulating the gating charge in the voltage gated ion channel of Kv1.216 and the voltage generation upon electron/proton transfer in the bacterial reaction center.19 The nonequilibrium direct approach also provided a new application of Brownian dynamics to simulate the gating current by solving kinetic master equation in a stochastic manner, based on a discrete kinetic model of channel conformations derived from the CG free energy profile.16
Recently, a rigorous theoretical framework that describes the kinetics/thermodynamics of voltage activation has been formulated based on statistical mechanical considerations,20 building on the refined CG model of the voltage coupling in membrane proteins.19 To rationalize and validate the energetics of the CG model of the voltage coupling, a linear response approximation was applied to the membrane/protein/electrolyte system, resulting in the capacitor-like voltage dependent quadratic free energies. The requirement that these free energies satisfy the equilibrium fluctuation relation21–23 yielded a novel closed-form expression of gating charge,20 consistent with the fluctuation–dissipation theorem.24 These voltage dependent energetics also offered a direct avenue to evaluate the Q–V curve, given two equilibrium conformational states. In addition, a simple quantitative relation between a free energy of stabilization or destabilization and a shift in the Q–V curve was introduced, which enables the relative free energies for the VSMP insertion into the membrane to be directly estimated from the shifts in the Q–V curve.25 Importantly, a novel expression for the free energy barrier (along with a chemical part of free energy change) at “zero” (depolarization) membrane potential was introduced in terms of the intrinsic properties of VSMP that are experimentally measurable.
The present study further explores our theoretical framework with a significantly more challenging problem, i.e., investigating VSMP activation in terms of the Q–V curve and the C–V curve with the full X-ray crystal structures of VSDs (Ci-VSD) derived from the Ciona intestinalis VSP (Ci-VSP).26 The present study also explores an applicability of the fluctuation–dissipation expression for the gating charge20 that characterizes voltage sensitivity of VSMP7,27 as well as the nonequilibrium direct approach16,17,19 that enables the gating charge directly evaluated, by considering the changes in the electrolyte distributions between the initial and the final configuration of VSMP. In this way, a nonequilibrium measurement of the gating charge is shown to be equal to an equilibrium measurement of charge fluctuations (i.e., voltage-independent linear capacitance) via temperature, as dictated by the fluctuation–dissipation theorem. We also offer alternative derivations for the key expressions, introduced in ref 20, such as the fundamental free energy relations of voltage activation and the fluctuation–dissipation relation for the gating charge. Importantly, we present novel derivations for the Eyring-type voltage-dependent rate equations. These provide closed-form expressions for the phenomenological parameters used for the (kinetic) descriptions of the gating current, membrane currents, and thus spikes in the Hodgkin–Huxley-type model.1,28–30
The paper is organized as follows: first, we describe our (extended) theoretical framework for the description of a kinetic and thermodynamic model of voltage coupling in membrane proteins, introducing resultant novel gating charge expressions and offering analytic derivations for voltage dependent energetics and rate constants (sections III and IV). We will use the CG simulation system with the energetics of voltage coupling of CG membrane proteins surrounded by electrolytes, which are connected to the electrodes, simulating the virtual battery (section II). Second, we present numerical simulations of the gating charge in both nonequilibrium and equilibrium ways and of the voltage dependent energetics of the Ci-VSD system that results in charge-voltage relationship (Q–V curve) and capacitance–voltage relationship (C–V curve) (sections V and VI).
II. COARSE-GRAINING (CG) MODEL OF VOLTAGE COUPLING IN MEMBRANE PROTEINS
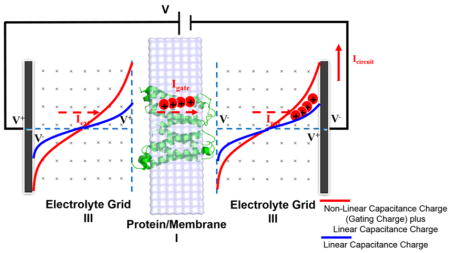
Our CG model of voltage coupling has been developed aiming at modeling the protein–membrane system and, in particular, its coupling to the external voltage.16–20 This model and its treatment of different dielectric constants is more reliable than continuum models as discussed and illustrated in many of our previous works.31 The CG simulation system includes the protein, membrane, grids representing electrolytes, and electrode potential, virtually simulating the external voltage (see Figure 1). The residual electrolyte charge ( ) and the electrical potential (φj) at each system grid are evaluated by solving two equations below eqs 1 and 2 in a self-consistent manner:18
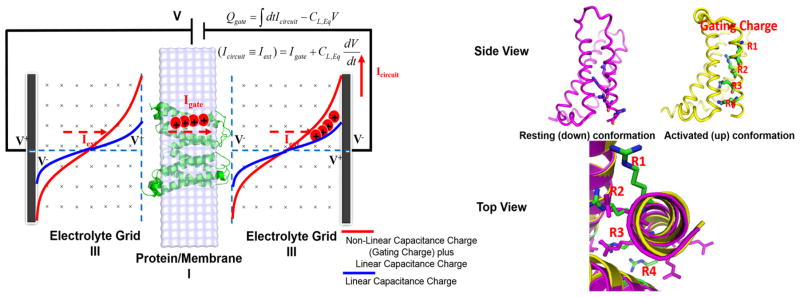
Figure 1.
(Left) CG simulation system for the membrane proteins coupled to the externally applied voltage. The simulation box includes the membrane containing the protein (region I), an optional region with explicit electrolytes (region II, which is not considered in the present study), a grid representing the electrolyte solutions (region III), and a “bulk region” far away from both the membrane and electrode surfaces, as a way for spanning the space between the membranes and the electrodes without using an enormous grid (which is not considered either in the present study). The CG model represents the solvent implicitly, while the ions in the solutions are considered more explicitly by using a grid-type approaches where the residual charges at each grid point represents the charges of the electrolytes ( ), which are determined self-consistently, as described in ref 18. The area formed by red and blue curves corresponds to the gating charge, as expressed by the RC parallel circuit relation applied to the gating current, . (Right) Resting (down) and activated (up) conformational states of Ci-VSD viewed from the side and the top (extracellular region). Upon depolarization (positive changes in the membrane potential), the arginine residues (designated as R1, R2, R3, and R4) in voltage sensor domains are displaced, due to the conformational changes from the resting state to the activated state, yielding the gating current that flows through a complete electric circuit, as shown on the left-hand figure.
| (1) |
| (2) |
where the units are kcal/mol rather than the esu units and distant dependent effective dielectric constants of 60 and 40 were used, respectively, for the (protein) charge–charge interactions ( ) and electrolyte response to the protein charges ( ).
To model the effects of the external potential, we treat formally the membrane/protein/electrolyte system as a capacitor using the macroscopic formula17,18
| (3) |
where Z0 is the Z coordinate at the left electrode.
The energetics of our CG model is based on the folding model of (membrane) proteins (ΔGfold) that focuses on reliable treatment of the electrostatic energy ( ), considering the Born-type self-energy and the charge–charge interaction of (protein) ionizable residues with realistic dielectrics. The energetics of CG model has been constantly refined,32 and the readers are referred to ref 31 for a recent refinement for the membrane protein system. In the present study, we only consider the electrostatic contribution ( ) in great details.
The state dependent (λ) electrostatic free energy is given by19,20
| (4) |
The first term represent the voltage-independent electrostatic free energy of the ionizable residues in electrolyte solutions, which is the sum of three contributions:
| (5) |
The first term corresponds to the local-environment dependent Born-type self-energy of protein ionizable residues and the second term to the charge–charge interaction energy, with a distant dependent dielectric that approaches 60 in an infinite distance. The last terms represents the coupling of protein charges to the polarized electrolytes. eq 5 is a grid-based representation of the free energy of ion solvation (i.e., Born solvation) in electrolyte solutions (e.g., as in the Debye–Huckel theory).
The second term, , in eq 4, represents the effects of the applied voltage on the energetics of the protein/ membrane/electrolyte system:
| (6) |
The first and second terms represent the contribution that arises from the polarization of electrolyte effective charges ( ) by the external voltage and all the other charges of the system. The third term represents the coupling of the protein charges ( ) to the membrane potential that arises from the external voltage.
In the absence of protein charges within the membrane, it was shown that there exists correspondence between the CG model of voltage coupling and macroscopic continuum models:20
| (7) |
Equation 4 with eqs 6 and 7, can be rewritten as follows, yielding the energetics similar to the that of the mean field macroscopic continuum approach:
| (8) |
Here CL,Eq is the equilibrium linear component of membrane capacitance (of the membrane protein system), which should be distinguished with the membrane capacitance of Ce in eq 7 defined in the absence of protein charges within the membrane (see section IV). The expression is familiar in the field of ion channels, having been used to describe the thermodynamics of voltage activation.9,10,20,33,34 In fact, eq 8 represents the energetics of the protein/membrane system, described by the Hamiltonian of H1 = H0 + QgVmem (see eq 42), which represents the coupling of gating charge carrying residues to the membrane potential ( ) that arises from the externally applied voltage (Vext). Whereas, eq 4 with eq 6 represents the energetics of the entire protein/membrane/electrolyte system, described by the Hamiltonian of H0 = H1 –Qext(Vext –V1,min) (see eq 30), which represents the interaction of electrolyte, coupled with the movement of protein charges within the membrane, with the externally applied voltage,20 where, V1,min is the resting (equilibrium) membrane potential. Here, H0 and H1 represents, respectively, the Hamiltonians of the activated and the resting states. Qg and Qext represents, respectively, the gating charge (coupled to the membrane potential) and the externally flowing charges (coupled to the external voltage) through electrolytes. In fact, the equivalent relation between the external charges (〈Qext〉) and the gating charge (Qg) can be given by the parallel RC circuit-like expression,20 as clearly shown in Figure 1:
| (9) |
For the gating current we have,
| (10) |
Eq 10 tells nothing but the law of current conservation, 9,10,35,36 which shows that the actual measurement of gating current (Igate) is made by recording the current in an electric circuit (Icircuit = Iext) and subtracting the linear component of a capacitance current ( ), i.e., the current required to charge the membrane capacitor with a membrane capacitance of CL,Eq, as done in the electrophysiological measurement of the gating charge.37 The subtraction of from the recorded current (Icircuit = Iext) implies a measurement of the gating current is a nonequilibrium process before the external voltage becomes stationary. Notice that eq 9 offers a formal justification for the gating charge evaluation by measuring the externally flowing charges (〈Q〉ext) through electrolyte solutions (i.e., the nonequilibrium direct approach16,17,19), as will be explored in section V. The state dependent external charges are defined as
| (11) |
where the linear component of membrane capacitance (CL,Eq) is assumed to equal before and after the conformational changes of VSDs, as in the electrophysiological measurement of the gating charge,37 which was justified by the linear response approximation.20 By subtracting the two equations, we have
| (12) |
which proves the equivalence of the two charges. The gating charge evaluation by our nonequilibrium direct approach (the right-hand side of eq 12) will be examined in section V using eq 63, i.e., by measuring the changes in the electrolyte distributions, given two quasi-equilibrium conformational states. Equation 12 also shows that a measurement of the gating charge, given two quasi-equilibrium resting and activated states, is independent of the voltage applied,14,19 due to the linear response approximation.20
III. GENERAL FREE ENERGY RELATIONSHIPS AND THE WORK–FLUCTUATION RELATION
In this section, we present several variants of free energy relationships1 used to account for the kinetics and thermodynamics of the voltage dependency of channel activation (e.g., Q–V curve), from a perspective of the theoretical framework of voltage coupling developed in ref 20. While doing so, we give alternative derivation of the fundamental free energy relation of voltage activation of eq 13. As discussed in ref 20, the externally applied voltage (Vext) is assumed to be equal to the membrane potential (Vm), which is represented by V in the present study, unless otherwise specified. Time integration of external current (〈Qext〉), flowing through electrolyte solutions, which is then recorded in an electric circuit, was also assumed to be equal to the movement of positively charges residues within the membrane, i.e., gating charge (Qg) coupled to the membrane potential as discussed in section II.
The two probability densities of either finding 0 (activated) or 1 (resting) conformations of voltage sensing domain (VSD) at an external voltage of V is related to each other:1
| (13) |
Here the Boltzmann constant kB = 1, and Qg and ΔGchem, respectively, represent the gating charge and the chemical part of free energy change associated with the conformational transition between the resting and the activated states, namely, the free energy difference between two states at “zero” (depolarization) membrane potential.38 The relation is termed here as the fundamental free energy relation of first kind.20 This fundamental free energy relation has been known to the ion channel community some time ago, e.g., as in Hille’s book,1 which goes back to Hodgkin and Huxley (HH) for their formulation to quantify membrane currents and thus action potentials (spikes) in a nerve cell39 (e.g., p0(V) corresponds to the gating variable of n∞(V) for a voltage-gated K+ channel in the HH model).
In the following, we offer a simple derivation of eq 13, which will then be discussed within the general theoretical framework of voltage coupling in membrane proteins that was developed based on the equilibrium fluctuation relation and the linear response approximation.20 Consider the HH kinetic model for VSD transition between the resting and the activated states of ion channels:39
| (14) |
Here C and O, respectively, represent the resting and activated conformations of VSD. α(V) and β(V) represent, respectively, forward and backward voltage dependent transition rates (rate constants). Here, we assume that each rate constant is a simple semiempirical Eying-type exponential of the externally applied voltage1,40,41 that starts initially at the resting membrane potential (Vr) rather than from 0 mV.
| (15) |
Here α(0) and β(0) are rate constant at “zero” (depolarization) membrane potential, which derived in the previous study, in terms of free energy barrier20 (see also section IV). Qg.c and Qg,o are state dependent gating charges. Vr and Vd, respectively, represent the resting and the (fully activated) depolarization membrane potentials, as V1,min and V0,min (see below).
The condition of dynamical equilibrium (or detailed balance) requires that
| (16) |
or
| (17) |
where Qg = Qg,c + Qg,o = zQg + (1 − z)Qg is the total gating charge associated with the conformational transition of VSDs from the resting to activated states. z is “a fraction” of charge (where 0 < z < 1) that represents the progression of charge movements normal to the membrane (i.e., voltage-dependent electrogenic movements19). In electrophysiological blocking experiment, z is served as an effective voltage dependent charge movement, obtained by fitting to the observed I–V curve.42 In fact, in chemical reactions, z has been used as a measure for the location of the transition state along a collective reaction coordinate.43 A value of 1/2, which produces a symmetric barrier, is often assigned for the thermodynamic/kinetic study of voltage-dependent electrogenic charge movements in ion pumps and transporters unless prior information exists.44 In the present study, an analytical expression for z will be derived in section IV, in terms of the intrinsic properties of VSMP activation. eq 17 results in the original fundamental free energy relation of first kind of eq 13 with
| (18) |
The fundamental free energy relation of first kind was derived in ref 20, directly from the Bennett overlapping histogram (BOH)21,23,45 or the equilibrium fluctuation relation.20 In fact, BOH is a special case of the more general nonequilibrium relation known as the work-fluctuation theorem:46,47
| (19) |
where W and W̄ are, respectively, forward and reverse works (regardless of whether the work is reversible or irreversible) that drive the system from the initial system (H0) to final system (H1 = H0 + W) and vice versa. The work–fluctuation theorem is thought to belong to a large class of fluctuation theorems.48–51
By introducing the voltage (coupling) as the work (energy gap in the previous study) reaction coordinate,20 i.e., W = QgV, eq 19 results in the fundamental free energy relation of first kind of eq 13, where ΔGrx is identified to ΔGchem.
At the intersection of two probability distributions, we have (QgV* ≡ QgV1/2) − ΔGrx = 0, leading to
| (20) |
where V1/2 is a half membrane potential at which two conformational states have equal population. ΔGrx will be defined in another way below, whose meaning will be discussed in the general theoretical framework that builds upon the work-fluctuation relation of eq 19.
Rearranging eq 19, together with eq 20, yielded the fundamental free energy relation of second kind,20 which is familiar in voltage gated ion channels:9,38
| (21) |
| (22) |
where the free energy functions, Δfλ(V){λ = 0,1}, or potential of mean force along the voltage work (energy gap) reaction coordinate, are defined as20,23
| (23) |
where and pλ,max is the maximum value of probability density such that Δgλ(Vλ,min) = 0, or equivalently, pλ(Vλ,min) = pλ,max. In addition, the free energy functions, Δfλ(V){λ = 0,1}, intersect at zero membrane potential, leading to the expression:
| (24) |
or
| (25) |
which is the explicit definition of the chemical component of free energy change (ΔGchem ≡ Δg0(0)−Δg1(0) = QgV1/2 = ΔGrx), i.e., the free energy difference between two conformational states at zero (depolarization) membrane potential.20,38 Together with eq 25, eq 22 yields a well-appreciated free energy relation40,44 that describes the voltage effects on the thermodynamics of VSMP activation along reaction coordinate(s) (e.g., a collective reaction coordinate of the gating charge movements in VSDs) (see Figure 2):
| (26) |
where Δg(V) = Δg0(V) − Δg1(V). This free energy relation is the first key expression of our paper. Note that while the voltage effects on the thermodynamics of voltage activation appear to be linearly dependent on an external voltage, the relation is actually exact up-to a second order of the external voltage, due to the linear response approximation20 (i.e., where the free energy functions have equal curvature for both the resting state and the activated state). A related expression that describes the voltage effects on the kinetics of voltage activation (voltage dependent rate constants) will be derived in section IV (see Figure 2).
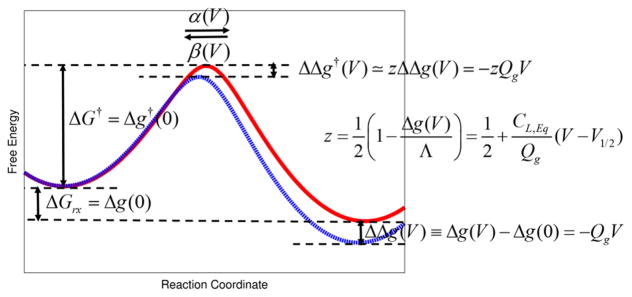
Figure 2.
Schematic illustration of the voltage effects on the thermodynamics (i.e., described by voltage-dependent equilibrium free energy change) and kinetics (i.e., described by voltage-dependent rate constants) of VSMP activation (gating). Two hypothetical (red and blue) free energy profiles are obtained by using the empirical valence bond (EVB) approach71,84 with Gaussian couplings. (Red) Free energy profile at “zero” (depolarization) membrane potential along a collective reaction coordinate of the charge movements in VSD. (Blue) Voltage-dependent free energy profile (i.e., voltage effects on the free energy profile of zero membrane potential). An application of positive voltage (membrane potential) stabilizes VSMP activation (stabilization of the activated state), whose quantitative relation is given by ΔΔg(V) ≡ Δg(V)−Δg(0) = −QgV, as in eq 26. The corresponding stabilization of the transition state is expressed by the linear-free energy relationship, given by ΔΔg†(V) ≃ zΔΔ(V) = −zQgV, as in eq 55, where analytic expression for the fraction of charge (z) is given by , as in eq 56. α(V) and β(V) are, respectively, the corresponding forward and backward voltage dependent rate constants eqs 61 and 62, related to each other via the fundamental free energy relation of first kind of eq 13 or the work-fluctuation theorem of eq 19). ΔGrx = Δg(0) and ΔG† = Δg†(0) represents, respectively, the free energy difference and the free energy barrier at “zero” depolarization membrane potential, given by eqs 25 and 26, and 55, respectively.
Last, ΔGrx was shown to be equivalent to the free energy difference between two “equilibrium” states along the voltage work (energy gap) reaction coordinate,20 using eq 23:
| (27) |
In fact, the chemical component of free energy change of eq 25 is equal to the free energy difference between two quasi-equilibrium states along the voltage energy reaction coordinate, leading to the fundamental free relation of third kind:20,23
| (28) |
A differentiation of eq 20 yielded the interesting expression of ΔΔGrx ≃ QgΔV1/2 for nongating charge carrying mutations, which correlates a shift in the half voltage of the Q–V curve (e.g., in response to site-directed mutation(s) or drug binding) to the free energy of destabilization or stabilization.20 The expression offer a new avenue to evaluate membrane-insertion free energies in voltage gated ion channels, directly from the experimental Q–V curve.25 Alternatively, the relative shifts in the Q–V, upon site-directed mutations or drug binding, can be examined by simulating the relative free energies of mutations, using both our CG model of membrane proteins31 and/or umbrella sampling enhanced all-atom molecular dynamics free energy perturbation (Bennett acceptance ratio).23,52
In closing this subsection, the caution should be exercised for the sign of the equilibrium free energy difference introduced in this section; as the free energy change is defined as the transition from the activated state to the resting state (i.e., deactivation) in eq 19, the “activation” equilibrium free energy difference (from the resting state to the activation state) is, thus, expressed by
| (29) |
However, we keep the original sign for a half voltage when the gating charge and the half voltage are evaluated from the Q–V curve (that describes the degree of voltage “activation”). That is, the chemical component of free energy change of eq 25 will be reserved for describing the Q–V curve (see section VI).
The free energy relationships investigated so far are illustrated in Figure 3 using the actual simulation results for Ci-VSD activation.
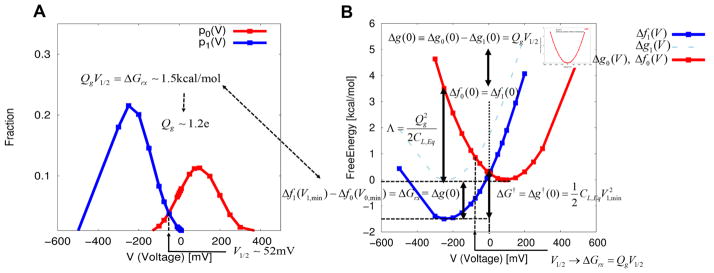
Figure 3.
Illustration of the fundamental free energy relation of the first kind of eq 13 (i.e., the work-fluctuation relation of eq 19) that yield the gating charge, the half voltage, and the equilibrium free energy difference between the resting and the activated states (equivalently, a chemical component of free energy change). An application of the linear response approximation to the membrane/protein/electrolyte system yields the electrolyte-based capacitor-like voltage dependent free energies and new expressions for the reorganization energy and the free energy barrier of voltage activation, in an analogous way with those from the Marcus theory of electron transfer. (A) Probability densities of finding each of the resting and activated state at different external voltages. These probabilities were obtained from the CG energetics using Pλ(V) ∝ exp(−Δfλ(V)).The intersection of two probabilities yields the half voltage (−V1/2) of 51. 90 mV at which the resting and activated states are equally probable. Notice that we have a minus sign for the real half voltage, as discussed in details in section III. Together with the equilibrium free energy difference of 1.45 kcal/mol, the formula of eq 29 yields a gating charge of ~1.2e. (B) Corresponding voltage dependent free energies reconstructed from the probabilities of part A using eq 23. The equilibrium free energy difference between the activated and resting states is shown to be equal to the chemical component of free energy change, whose relationship is summarized by eq 28. Notice that the equilibrium free energy difference is obtained by shifting the reference function of Δg1(V) in such a way that two free energy functions (Δfλ(V){λ = 0,1}) intersect at zero voltage eq 24, while the fundamental free energy relation of first kind of eq 13 (i.e., the work-fluctuation relation of eq 19) offers an alternative means to evaluate the equilibrium free energy difference. The voltage dependent free energy of Δf0(V) is reduced to the simple free energy of charging membrane capacitor of eq 31 in the absence of protein charges within the membrane, as shown in the inset.
IV. THERMODYNAMICS AND KINETICS OF GATING CHARGE FLUCTUATIONS
In this section, we present several different expressions for the gating charge and examine the correlations between them. In particular, we focus on the newly introduced gating charge expression,20 discussed in more details, offering a simple alternative derivation for the new gating charge expression. More importantly, an extension of our kinetic/thermodynamic model of voltage dependent activation in VSMP allows for novel derivations for the (somewhat) phenomenological Eyring-type voltage-dependent rate constants, whose parameters are expressed by the intrinsic properties of VSMP.
We have shown20 that our coarse-grained (CG) energetics of voltage coupling yields “capacitor-like” quadratic free energy functions eq 6 or 8, which in fact can be described by the Hamiltonian of H0 = H1 − Qext(V − V1,min), considering the electrolyte polarization coupled to the external voltage in the presence of protein charges within the membrane:20
| (30) |
where λ = {0,1} represent the activated and the resting states, respectively and. The validity of the free energy expansion up to second order as a function of the externally applied voltage was justified by the linear response approximation that any system of free energy of charging (by the external voltage in the present study) should be satisfied along a chosen reaction coordinate.20 Notice that the voltage dependent free energy, in the absence of protein charges within the membrane, is reduced to the well-known macroscopic free energy of charging membrane (capacitor) between two electrolytes,20 as in eq 7:
| (31) |
where Ce = −T−1〈δQelec2〉Vλ,min is the capacitance of the membrane between two electrolytes with
| (32) |
where is the capacitance of the membrane-only system, and 1/k, εm, εw, A, and L are, respectively, Debye length, dielectric constant of the membrane and water, and area and width of membrane. The correspondence between our CG model of voltage coupling and macroscopic continuum electrostatic model dictates the energy conservation that the free energy stored in the membrane capacitor is equal to the free energy of polarizing electrolyte solutions, by the externally applied voltage.
A novel expression for the gating charge was also derived, requiring the application of linear response approximation to the free energy functions of eq 30 should satisfy the fundamental free energy relation of first kind of eq 13 (i.e., the work-fluctuation theorem of eq 19) or the fundamental free energy relation of second kind of eq 21, yielding the following expression:20
| (33) |
where CL,Eq = −T−1〈δQext2〉Vmin is the linear (i.e., voltage independent) “equilibrium” capacitance of the membrane protein system as defined in eq 8, which is actually equivalent to an expression of the Johnson-Nyquist fluctuation–dissipation relation,35,53–55 i.e., 〈δV2〉Vmin = T/CL,Eq (see ref 56 for its relevance to the simple electrochemical double layer capacitor). As discussed in section II, the equilibrium capacitance of CL,Eq differs from the capacitance of the membrane-only (with electrolytes) capacitance of Ce without protein charges within the membrane. That is, the equilibrium capacitance of CL,Eq reflects the charge distributions of VSMP in their respective quasi-equilibrium states, with a minimal influence of the gating charge displacements. ΔVmin = V0,min − V1,min is the equilibrium membrane potential difference between the (fully activated) depolarization potential and the resting potential of VSMP. In fact, eq 33 represents the fluctuation–dissipation relation for “the gating charge”, where a nonequilibrium measurement of the gating charge is connected to an equilibrium measurement of charge fluctuations (i.e., the voltage-independent linear capacitance) via temperature. This point is discussed below in details.
The state dependent gating charge is defined from eqs 33 and 3020 as
| (34) |
The state dependent gating charge, as discussed in section II and in ref 20, is assumed to be equal to the externally flowing charges in a complete circuit, i.e., Qg,λ = 〈Qext〉λ, which then leads to
| (35) |
The relation may be rewritten in a differential form:
| (36) |
as also implicated in eq 30.20 Therefore, eq 36 clearly represents the fluctuation–dissipation relation for “the gating charge” in VSMP (see below).
Now, notice that the gating charge can be written as an integral of the voltage dependent nonlinear capacitance of CNL,Neq (i.e., nonlinear capacitance charge) over the voltage range where the gating charge is measured:
| (37) |
Using eq 33, we have
| (38) |
Rearrangement of eq 38 yields
| (39) |
where ΔVmin = V0,min − V1,min and Vc is some voltage between V1,min and V0,min.
Here, the mean value theorem in calculus was used in the last equality, where an equilibrium measurement of the linear (i.e., voltage-independent) capacitance is connected to a non-equilibrium measurement of the nonlinear (i.e., voltage-dependent) capacitance, as predicted by the fluctuation–dissipation theorem. The relation is the second key expression of our paper, probably giving an alternative avenue to measure the linear component of membrane capacitance (CL,Eq) in VSMP. The threshold voltage (Vc) defined in eq 39 may be related to the onset of the rising phase of gating current.16 For example, it is known that for a weak applied voltage, the gating current is described by a single exponential-like kinetics, as dictated by the “equilibrium” fluctuation–dissipation theorem. This simple kinetics is independent of the number of conformational states of VSDs used to build, e.g., Markov state models and solve the kinetic master equation, as long as the initial barrier for VSMP activation is the highest.16,57,58 However, for a strong applied voltage, the gating current is described by multiexponential kinetics in order to capture the rising phase of the gating charge.16,59,60 In this case, it is unclear whether the “equilibrium” fluctuation–dissipation theorem holds,61,62 while the magnitude of the gating charge may be still evaluated by using eq 33. The study of this point is left for further investigations.
Next we consider several different forms of the gating charge to explore their connections to the conventional (state dependent) gating charge expression.9,34,35
The state dependent gating charge of eq 34 also imply the following relation via eq 30:
| (40) |
leading to another gating charge expression of the form:
| (41) |
Here, we note that the new gating charge expression of eq 33 can be obtained by writing another equivalent relation to eq 30:9,33,34
| (42) |
That is, a comparison of eq 42 with eq 30 yields the same expression as eq 34, thereby leading to the same gating charge expression as eq 33.
The state dependent gating charge (Qg,λ) in eq 42 is given by ref 9
| (43) |
where δλ,j represents the coupling of protein charges (qj) to the membrane potential (ϕλ(xj)) that arises from an external voltage of V:
| (44) |
δλ,j is often called dielectric distance, which represents a fraction of membrane potential (0 < δλ,j < 1) that falls on the jth charged amino acid (qj).9,34,44 Assuming the linear dependency of the membrane potential (ϕλ(xj)) on the eternal voltage,10 i.e., ϕλ(xj) = Vϕmp,λ(xj), the state dependent gating charge of eq 43 leads to the well-known mean field macroscopic continuum expression:10
| (45) |
The corresponding gating charge is then given by
| (46) |
Because of the assumption of a linear dependency of the membrane potential (ϕλ(xj) = Vϕmp,λ(xj)), a fraction of membrane potential of ϕmp,λ(xj) should, then, take a simple geometrical expression44 (see also ref 20 and references therein), given by
| (47) |
Therefore, it is not strictly required to solve the Poisson–Boltzmann equation as in ref 10 for the membrane potential of ϕmp,λ(xj); however, the determination of local dielectric constants is rather critical (note that the local dielectric constants can be also evaluated by microscopic simulations63).
Equation 45, together with eq 47 yields, then, the gating charge of the form
| (48) |
where Δzj, a distance traveled by the charge of qj defined normal to the membrane axis. εL and εj are, respectively, the dielectric constant of the membrane and the average local dielectric constant around the region of Δzj. Equation 48 has been often exercised with uniform dielectric constants in the macroscopic continuum approach64 and in the all-atom molecular dynamics simulations to approximately evaluate the actual gating charge.14,15
The polarization of the system (Pλ) is given by the following equation from ref 9:
| (49) |
Notice that eq 42 may be obtained by expanding the free energy function of voltage up-to second order by considering the protein/membrane system only, i.e., the coupling of protein charges (gating charge) to the membrane potential, described by the Hamiltonian of Ho = Hc + QgV. That is, using the CG energetics of eq 8, the state dependent on gating charge of eq 40 yields another expression (with the linear dependency assumption of membrane potential on the external voltage):
| (50) |
which was conjectured in ref 20, which can be also obtained by equating eq 8 and eq 42. The gating charge is then given by
| (51) |
In fact, this gating charge expression was rigorously derived, based on the Ramo–Shockley theorem,36 which is the same expression as eq 46 with . is then identified as φλ(xj) in eq 44.
Considering the observation that we have quadratic Marcus-type free energies of equal curvature, which is reflected by the capacitance (as turned out to be true for the gating charge measurement37), the reorganization energy of Λ = Λ0→1 = Λ1→0—the energy required to “reorganize” the environment (e.g., solvent and electrolyte polarization) from initial to final states, given a fixed initial conformational state and vice versa (see Figure 3B)—is expressed as
| (52) |
where 〈W〉λ ≃ Qg〈V〉λ. By subtracting the two equations in eq 52, we have a well-known linear response expression for the free energy difference between two states:65
| (53) |
Together with ΔVmin ≡ V0,min − V1,min = 〈V〉0 − 〈V〉1, eq 53 yields the closed-form expression for the reorganization energy:
| (54) |
whose expression resembles a capacitor-like free energy of charging the membrane but with “the gating charge”.
Notice that the reorganization energy defined in eq 52 is identified as the dissipated work or total entropy production (multiplied by temperature) in (statistical) thermodynamics, whose forward and reverse probability distributions satisfy the work-fluctuation relation of eq 19 (or its extended fluctuation theorem, i.e., the entropy production fluctuation theorem ref 22), constrained by the second law of thermodynamics in a macroscopic sense. It would be interesting to examine how the total entropy production is related to the existence of the inverted region where the reaction rates (here the rates of conformational changes) decreases with increasing the exergonicity of the reaction, as in the Marcus theory of electron transfer.
The identification of the reorganization energy of eq 52 as the total entropy production (multiplied by temperature) results in the well-known Gibbs-Bogoliubov inequality (see ref 21), which is nothing but a statement of the second law of thermodynamics:
Given the reorganization energy of eq 54, and the reaction free energy of eq 20 we introduced a closed-form expression for the free energy barrier of VSMP activation at “zero” (depolarization) membrane potential (see Figure 3B), given by20
| (55) |
where we have changed the sign of ΔGrx, i.e., ΔGrx = −ΔGrx to describe the “activation” of VSMP, as discussed in section III. The last equality comes directly from eq 58. The free energy barriers at “zero” (depolarization) membrane potential using eq 55 were estimated to yield ~13.7 kcal/mol and ~7.3 kcal/mol for Shaker and Kv.1.2, respectively.20 Notice, however, these values are subject to changes to lower ones due to the linear coupling assumption.66,67 eq 55 will be examined to estimate the free energy barrier for Ci-VSP transition at “zero” (depolarization) membrane potential (see Figure 3 and section VI). However, it has yet to be clarified that the free energy of barrier associated with the reorganization energy may not be the barrier for moving the charge across the membrane. In fact, this barrier may be associated with moving the electrolytes, and solvent between their two configurations that stabilize the two charge configurations. In other words, this barrier and the corresponding reorganization are conceptually similar to the corresponding results obtained in electron transfer when the donor and acceptor are kept at a fixed distance. The relationship between the above barrier of the “capacity reorganization” and the barrier for the protein reorganization can be better addressed with real proteins and this important issue will be further discussed below. It will be of course interesting to explore the contribution to this barrier from the reorganization of the protein polar groups in real membrane proteins, using microscopic estimates.
Given the free energy barrier expression of eq 55 at “zero” (depolarization) membrane potential, we now present an analytical derivation for the semiempirical Eyring-type voltage-dependent rate constant expression that describes the voltage effects on the kinetics of VSMP activation (gating). The voltage dependent free energy barrier projected along a collective reaction coordinate of the charge movements in VSDs can be expressed as (see Figure 2):
| (56) |
where z is defined as
| (57) |
where we have used eq 26. These two equations are the third key expressions of our paper, where z represents the same fraction of charge defined in eq 15 (see below), which may be also related to a fraction of membrane potential of eq 47. For V = V1/2, we have z equal to 1/2 as expected, as the resting state and the activated state have equal population at this voltage, reflecting a symmetric barrier.40,44,68 In fact, eq 56 is known as a linear-free energy relationship69–72 (between a reaction free energy and a free energy barrier) in physical organic chemistry (i.e., Hammett equation72) that has been commonly used in analyzing the effects of substituents on organic reactions and of mutations on enzymatic reactions.73–76 A linear-free energy relationship is also called as Bronsted slopes43 that describe the position of the transition state (or degrees of the progression for the general chemical reactions). Since z lies between 0 and 1 (0 < z < 1), notice that the qusi-equilibrium (minimum) membrane potentials for the resting and activated states are, respectively, given by
| (58) |
A general expression for a voltage dependent “rate constant” for VSMP is given by
| (59) |
Using eq 56, we have
| (60) |
which is the same expression as eq 15 but the empirically introduced fraction of charge is now expressed as in terms of the intrinsic physiochemical properties of VSMP, as given by eq 57.
The voltage dependent rate constants can be then expressed as, using eq 57:
| (61) |
Similarly for β(V), we have
| (62) |
where the rate constants at “zero” (depolarization) membrane potential are α(0) ∝ exp(−ΔG†) and β(0) = α(0) exp(ΔGrx/ T) = α(0)exp(ΔGchem/T) with ΔG† = Δg†(0) in eq 55.20 Notice that these two equations are related to each other via the fundamental free energy relation of first kind of eq 13 (i.e., the work-fluctuation theorem of eq 19), as also expected from the detailed balance condition of eq 16:
All of the kinetic/thermodynamics free energy relations derived in the present study, along with a collective reaction coordinate of the charge movements in VSDs, are shown in Figure 2. Equations 61 and 62 provide a firm physicochemical foundation for the semiempirical expressions for the (nonlinear quadratic) kinetic/thermodynamic model of voltage dependent gating in VSMP1,28,33 that has long been used to describe voltage-dependent membrane currents and spikes in the Hodgkin–Huxley-type model.
V. NUMERICAL SIMULATIONS OF GATING CHARGES
Our first approach for evaluating the gating charge (called the nonequilibrium direct approach) is based on the CG model of voltage coupling, which is described in details elsewhere.18,20 Briefly, the CG simulation system includes a simulation box that explicitly includes the membrane containing the protein (region I) and a region representing grids of the electrolyte solutions (region III). In essence, we model the membrane protein system (that include electrolytes) and its interaction with the external voltage (see Figure 1). The two X-ray crystal structures of VSDs are taken from PDB 4G80 and 4G7V,26 which corresponds to the resting state and activated state, respectively. The positioning (as well as depth) of the membrane for VSDs is determined using the OPM database.77 The atomistic simulation systems of VSDs in a lipid bilayer of POPC were constructed using CHARMM-GUI.78 A 10 ns molecular dynamics run using CHARMM program79 (c38b1 version) was carried out for each simulation system (see refs 23 and 42 for detailed system setup and parameters). The CG protocol of MOLARIS program80 was subsequently used to build the CG model of the membrane protein system (that include electrolyte and electrodes). A 100 000 Monte Carlo step for the determination of the protonation state of the CG ionizable residues (of membrane proteins) was carried out to evaluate the voltage dependent free energies, by applying external potentials in the presence of electrolyte.
The nonequilibrium direct approach evaluates the actual gating charge by measuring the externally flowing charges through electrolyte solutions that arises from the movement of positively charge residues in VSDs discussed in section II, rather than indirectly determines it using the coupling of displaced positive charged residues within the membrane to the membrane potential.16,17,20 The CG simulation system represents the solvent implicitly, while the ions in the solutions are considered more explicitly by using a grid-type approaches where the residual charges at each grid point represents the charges of the electrolytes ( ), which are determined self-consistently, as described in ref.18 The model allows us to evaluate the actual charge distribution of the electrolytes associated with the conformation transitions of VSDs, and the changes in the corresponding cumulative charges (i.e., the gating charge), is given by
| (63) |
where ΔΔqgrid is the difference in the accumulative sum of Δqgrid before and after charge translocation, and Z′ is the point to the left of Z where the electrolyte charge distribution near the membrane changes sign. Figure 4A shows the gating charge determined by such a direct procedure, while using eq 63, yielding a gating charge of ~0.80e. The (total) gating charge, evaluated in this way (given two quasi-equilibrium states), is independent of the external voltage,14,19 due to the linear response approximation,20 as discussed in section II; the integrated (accumulated) charge in Figure 4A was produced at zero voltage.
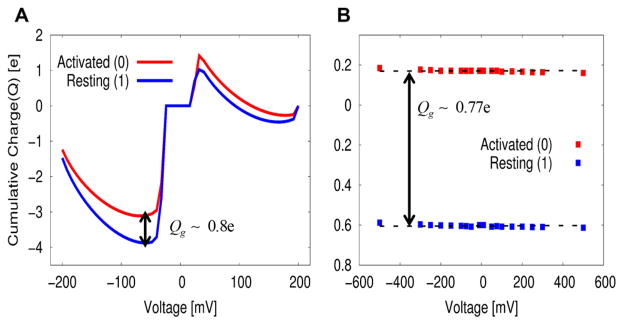
Figure 4.
Comparison of the gating charge between (A) our nonequilibrium direct approach of eq 63 and (B) the indirect approach of eq 51 whose expression is analogous to the mean field macroscopic continuum expression (see eqs 46 and 48). (A) Changes in electrolyte distributions between the resting (1) and the activated state (0) yields a gating charge of ~0.85e. (B) Linear least-square fit of state dependent gating charge for each resting and activated state gives approximately zero slope, yielding a gating charge of ~0.77e, where the linear component of capacitance charge (CL,EqV) for both states was automatically subtracted (see eq 12), unlikely the electrophysiological measurement of gating charge in ref 37, where a subtraction of linear component of capacitance charge is require eq 9. This indirect approach seems to underestimate the observed gating charge of ~1e and smaller than those gating charges (that range from 0.80e to 1.2e) estimated from several different approaches in section V and VI.
The second approach uses the fluctuation–dissipation expression for the gating charge derived both in ref 20 and in the present study (Qg = CL,EqΔVmin; see eq 33), using the minimum voltage difference between the resting and the activated states and the capacitance of the system. As shown in Figure 3, the voltages in the minimum of the resting state and the activated state are, respectively, −250 mV and +75 mV (while interpreted as −75 mV and +250 mV for the Q–V curve; see section VI), yielding ΔVmin = 325 mV.
The capacitance of the model system, i.e., charge fluctuations flowing through a complete circuit, can be estimated as a second derivative of the voltage dependent free energies with respect to an external voltage, yielding a capacitance of ~2.60e/ V (0.65 μF/cm2 with the membrane width of 80 × 80 Å). Thus, the fluctuation–dissipation expression for the gating charge (Qg = CL,EqΔVmin) yields a gating charge of ~0.85e, which is consistent with the nonequilibrium direct approach (above). Employing another form of the gating charge expression of eq 41 yields the same gating charge of ~0.85e.
The third approach uses the expression of eq 51 derived from our CG energetics for the voltage coupling, by asking its correspondence to the mean field macroscopic continuum approach.9,10,34 As used in the macroscopic continuum approach64 and the atomistic simulation,14,15 this approach yields a gating charge of ~0.77e, as shown in Figure 4B.
VI. NUMERICAL SIMULATIONS OF FREE ENERGY RELATIONS AND VOLTAGE DEPENDENCY OF CI-VSD ACTIVATION
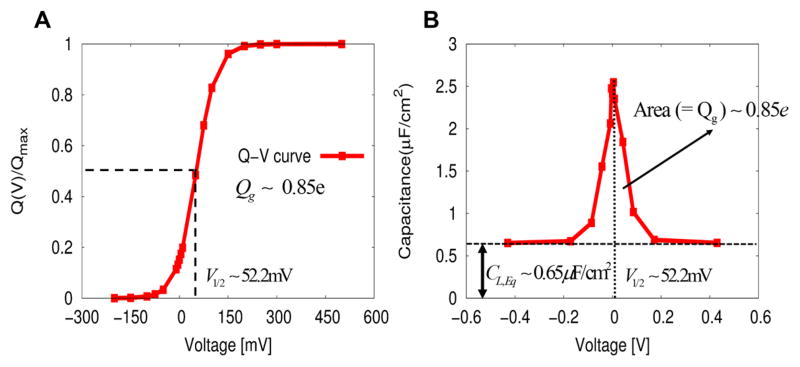
Although we explored the performance of our model in the hypothetical case of moving a charge between both sides of the membrane,20 it is much more challenging and convincing to explore the results for a realistic system. Thus, we present in Figure 3 the voltage dependent CG energetics associated with the conformational transition, from the activated (0) to the resting states (1), of VSDs from C. intestinalis. (Ci-VSP).26 The two probability densities, having a particular value of voltage are, shown in Figure 3A, are calculated by using pλ(V) ∝ exp(−Δfλ(V)), where the state dependent free energy functions of Δfλ(V) are obtained using the voltage dependent CG energetics of eq 4. The two probability densities are related to each other via the fundamental free energy relation of first kind of eq 13 or the work-fluctuation relation of eq 19, leading to a half voltage (−V1/2) of 51.90 mV at their intersection eqs 20 and 29. Figure 3B shows the corresponding free energy functions reconstructed from the probability densities in Figure 3A using eq 23. The voltage dependent free energy parabola is reminiscent of that from the Marcus theory of electron transfer, but the energetics of our CG model is evaluated by a “microscopic” consideration of electrolyte in the presence of applied voltage with VSDs within the membrane. The parabolic dependency of the energetics for voltage activation is a realization of the linear response approximation,20 as in eq 30. In fact, our CG free energy parabola is reduced to the simple free energy of charging (membrane) capacitor between two electrolyte solutions without any charge within the membrane (inset in Figure 3B), as in eq 31. The activation free energy difference between the two quasi-equilibrium conformational states, along the reaction coordinate of voltage (coupling), is about 1.45 kcal/mol. The corresponding gating charge is about 1.2e using eq 29. Notice that this free energy difference is obtained by shifting the reference function of Δgc(V) in such a way that two free energy functions (Δfλ(V){λ = 1,0}) intersect at “zero” (depolarization) membrane potential, as in eq 24. As formulated in eq 28, this equilibrium free energy difference is equal to a chemical component of free energy change (ΔGchem ≡ Δg0(0) − Δg1(0)) of ~1.0 kcal/mol using the formula of ΔGchem = QgV1/2 with Qg = 0.85e and V1/2 = 52.2 mV obtained from the Q–V curve (see Figure 5A), by a curve fitting using the following expression:
| (64) |
where pλ(V) ∝ exp(−Δfλ(V)). Notice that the gating charge of Qg (evaluated from the Q–V curve) is equal to the actual maximum gating charge of only for the two state model. As discussed in section III, the half voltage (evaluated from the Q–V) has a positive sign, compared to a negative one obtained from the fundamental free energy relation of first kind of eq 13 (or equivalently, the work-fluctuation relation of 19) (see also Figure 3), as the application of Q–V curve involves the transition from the resting state to the activated state (“activation”). For the half voltage of V1/2 > 0, the activated state is then less stable than the resting state in terms of the equilibrium free energy difference, as clearly shown in Figure 3B. The magnitude of the gating charge that was determined this way appears to be consistent with those estimated from the equilibrium free energy difference (1.2e), the several different approaches examined in section V, as well as the observed gating charge of ~1e.26 Furthermore, the half voltage of 52.2 mV from the Q–V curve is consistent with that (51.9 mV) obtained from the intersection of two probability densities using the fundamental free energy relation of first kind of eq 13 (i.e., the work-fluctuation theorem of eq 19) (see Figure 3A) and is in a good agreement with an observed half voltage of 58 mV.26 Figure 5B shows the voltage dependent nonlinear capacitance profile (C–V curve), obtained by differentiation of the un-normalized Q–V curve of Figure 5A. The voltage dependent nonlinear capacitance, whose integration yields the gating charge, originate from the structural changes of electrolytes, associated with the conformational changes of Ci-VSD (i.e., reflecting the voltage-dependent changes in equilibrium population). The curve presents a graphical representation of the fluctuation–dissipation relation for the gating charge: the more responsive is the gating charge to voltage changes (which is related to the equilibrium fluctuation of charges, i.e., voltage-independent linear capacitance), the voltage-dependent nonlinear capacitance, measured in a nonequilibrium state, has a shaper shape and a larger area in the smaller ranges of voltage, as expressed by eq 36.
Figure 5.
(A) Voltage dependency of Ci-VSD activation (Q–V curve) obtained directly from the CG voltage dependent energetics. The least-square fit to the voltage dependent open (activated) probability (ref.20) yields a half voltage of 52.2 mV and a gating charge of ~0.85e. This value of half voltage is a good agreement with an observed half voltage of 58 mV26 and is consistent with that obtained from the intersection of two probability densities using the fundamental free energy relation of first kind of eq 13 (i.e., the work-fluctuation theorem of eq 19) (see Figure 3A). A gating charge of ~0.85e is also in a good agreement with an observed value of ~1e and is consistent with those estimated from the equilibrium free energy difference (~1.2e) using eq 29 and several different approaches examined in section V. (B) Nonlinear voltage dependent capacitance (CNL,Neq), associated with structural changes of electrolytes, reflecting the conformational changes of Ci-VSD. The nonlinear voltage dependent capacitance is obtained from the “un-normalized” Q–V curve from part A. The nonlinear voltage dependent capacitance is shifted upward by the linear voltage independent capacitance (CL,Eq) of 0.64 μF, yielding the “total” capacitance of the system, as shown in the figure. The area, formed by a curve of the nonlinear voltage dependent capacitance and a line of the linear voltage independent capacitance of CL,Eq = 0.64 μF, is equal to the gating charge (Qg) of ~0.85e. An equilibrium measurement of the linear component of capacitance (CL,Eq) is related to a nonequilibrium measurement of the nonlinear component of voltage dependent capacitance (CNL,Neq), via the mean value theorem in Calculus eq 39), as dictated by the fluctuation–dissipation theorem for the gating charge (eq 36).
Finally we note that the CG free energy barrier at “zero” (depolarization) membrane potential is around 1.7 kcal/mol (see Figure 3B), which is consistent with a value of ~1.9 kcal/ mol estimated by the analytic expression of eq 55. However, it should be yet clarified that the free energy of barrier associated with the conformational change of VSD is not at all the barrier for moving the charge across the membrane. In fact, the barrier is associated with moving the electrolytes, and solvent between their two configurations that stabilize the two charge configurations. This barrier and the corresponding reorganization are conceptually similar to the corresponding results obtained in electron transfer when the donor and acceptor are kept at a fixed distance. It would be of course interesting to explore the contribution to this barrier from the reorganization of the protein polar groups in a real membrane protein, using both CG and microscopic estimates.
VII. CONCLUDING REMARKS
Correlating the structural information on the membrane proteins with electrophysiological measurements poses great challenges in computer simulations of voltage sensitive membrane proteins (VSMP). In the present study, we tackled one of these challenges by applying the coarse-graining (CG) model for the voltage coupling in membrane proteins to simulating the voltage dependency of VSMP activation (Q–V curve and C–V curve), taking the VSDs (Ci-VSD) derived from the C. intestinalis voltage sensitive phosphatase (Ci-VSP) as a model system.
Using the CG free energies as a function of the voltage for both the resting and activated conformational states of the VSDs, we have presented a novel structure-based energy landscape approach that allow us to simulate, in a straightforward manner, the voltage dependent Ci-VSD profile, characterized by the Q–V curve and the C–V curve. To best our knowledge, our approach is the first computational realization of the C–V curve and the Q–V curve that uses the full X-ray structural information on VSDs (see also ref.11). The gating charge and the half voltage obtained from the Q–V curve are consistent with those obtained from the voltage free energy parabolas of the resting and activates states by using the fundamental free energy relation of first kind (or the work-fluctuation relation) (see also Figure 3). By using the reaction coordinate of the voltage work (energy gap) for both the free energy landscape and the Q–V curve, our approach offers what seem to us to be a much clearer quantitative correlation between them.
A close inspection of the Q–V correlation from eq 20 allows for an estimate of the effects of mutations on the energetics of voltage activation and the corresponding shifts in the Q–V curve. That is, the simple relation of ΔGrx,chem = QgV1/2,20 for nongating charge carrying mutations, offers a new avenue for estimating the relative free energies for the VSMP insertion into the membrane from the shifts in the Q–V curve.25 This relevant free energy change, which can be induced by mutational experiments, can be examined by both using our CG model of membrane proteins (ref 31) and/or umbrella sampling enhanced (for slow degrees of freedom) all-atom molecular dynamics free energy perturbation (Bennett’s acceptance ratio).23
The CG model for the voltage coupling also provides a nonequilibrium direct way to calculate the gating charge, by measuring the changes in electrolyte distributions using the resting and activated states, providing a clear picture of the nature of the gating charge. In addition, the equivalence by the law of energy conservation between the membrane/protein system (described by the coupling of gating charge-carrying residues to the membrane potential) and the membrane/ protein/electrolyte system (described by the coupling of electrolyte to the external voltage) results in a new expression for the gating charge, expressed as the intrinsic properties of VSMP. The new expression of the gating charge, which is related to charge fluctuations (i.e., voltage-independent linear equilibrium capacitance) flowing through electrolyte solutions, turns out to be the fluctuation–dissipation relation (see ref 24 for a review) for the gating charge in VSMP. In some respect, our expression could be regarded as a generalized version of the Johnson–Nyquist relation that includes the gating charge within the membrane capacitor. The new expression provides a physically clear description of the gating charge as a measure of the voltage sensitivity of ion channels,7 and brings novel insights into the nature of the gating charge, by uncovering the connection between an equilibrium measurement of the voltage-independent linear capacitance and a nonequilibrium measurement of the voltage-dependent nonlinear capacitance eq 39. The relation may give a criterion to what extend the “equilibrium” fluctuation–dissipation theorem can be applicable to the nonlinear systems.61,62
Importantly, we have provided a physicochemical foundation for the Eyring type semiempirical (kinetic) descriptions of the gating current and membrane currents, by offering rigorous derivations for voltage dependent rate constants that have long been used for the phenomenological (kinetic) descriptions of membrane and gating currents. Together with the previous study,20 our extended theoretical framework provides new insights into the kinetic/thermodynamic model of voltage dependent gating in ion channels as well as voltage dependent electrogenicity in transporters. The developed theoretical framework may have potential implications on the roles played by gating charge fluctuations for the spike generations in the Hodgkin-Huxley-type model.29,30,81
In the future, our CG system for the voltage sensitive membrane proteins will be extended to a more microscopic direction for the model of electrolyte (from a grid-based to an explicit representation). In this way, the extended CG model may offer a true microscopic perspective to our capacitor model of voltage activation in VSMP as well as electrogenic transitions in proton pumps19 and transporters. The extended simulation protocols may find many electrochemical/electronic applications such as supercapacitors82 and electrolyte-gated transistors, 83 possibly taking advantage of the high voltage sensitivity of voltage gated ion channels.27
Acknowledgments
This work was supported by the NIH grant GM40283, the National Science Foundation Grant MCB-1243719. We acknowledge the University of Southern California’s High Performance Computing and Communications Center for computer time.
Footnotes
Notes
The authors declare no competing financial interest.
References
- 1.Hille B. Ion channels of excitable membranes. Vol. 507 Sinauer; Sunderland, MA: 2001. [Google Scholar]
- 2.Sakmann B. Single-channel recording. Springer Science & Business Media; 2013. [Google Scholar]
- 3.Murata Y, Iwasaki H, Sasaki M, Inaba K, Okamura Y. Phosphoinositide phosphatase activity coupled to an intrinsic voltage sensor. Nature. 2005;435:1239–1243. doi: 10.1038/nature03650. [DOI] [PubMed] [Google Scholar]
- 4.DeCoursey TE, Morgan D, Cherny VV. The voltage dependence of NADPH oxidase reveals why phagocytes need proton channels. Nature. 2003;422:531–534. doi: 10.1038/nature01523. [DOI] [PubMed] [Google Scholar]
- 5.Ramsey IS, Moran MM, Chong JA, Clapham DE. A voltage-gated proton-selective channel lacking the pore domain. Nature. 2006;440:1213–1216. doi: 10.1038/nature04700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Armstrong CM, Bezanilla F. Inactivation of the sodium channel. II. Gating current experiments. J Gen Physiol. 1977;70:567–590. doi: 10.1085/jgp.70.5.567. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Schoppa NE, McCormack K, Tanouye MA, Sigworth FJ. The size of gating charge in wild-type and mutant Shaker potassium channels. Science. 1992;255:1712–1715. doi: 10.1126/science.1553560. [DOI] [PubMed] [Google Scholar]
- 8.Jiang Y, Ruta V, Chen J, Lee A, MacKinnon R. The principle of gating charge movement in a voltage-dependent K+ channel. Nature. 2003;423:42–48. doi: 10.1038/nature01581. [DOI] [PubMed] [Google Scholar]
- 9.Sigworth FJ. Voltage gating of ion channels. Q Rev Biophys. 1994;27:1–40. doi: 10.1017/s0033583500002894. [DOI] [PubMed] [Google Scholar]
- 10.Roux B. Influence of the membrane potential on the free energy of an intrinsic protein. Biophys J. 1997;73:2980. doi: 10.1016/S0006-3495(97)78327-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lecar H, Larsson HP, Grabe M. Electrostatic model of S4 motion in voltage-gated ion channels. Biophys J. 2003;85:2854–2864. doi: 10.1016/S0006-3495(03)74708-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Roux B. The membrane potential and its representation by a constant electric field in computer simulations. Biophys J. 2008;95:4205–4216. doi: 10.1529/biophysj.108.136499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Delemotte L, Tarek M, Klein ML, Amaral C, Treptow W. Intermediate states of the Kv1. 2 voltage sensor from atomistic molecular dynamics simulations. Proc Natl Acad Sci U S A. 2011;108:6109–6114. doi: 10.1073/pnas.1102724108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Khalili-Araghi F, Jogini V, Yarov-Yarovoy V, Tajkhorshid E, Roux B, Schulten K. Calculation of the gating charge for the Kv1. 2 voltage-activated potassium channel. Biophys J. 2010;98:2189–2198. doi: 10.1016/j.bpj.2010.02.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jensen MØ, Jogini V, Borhani DW, Leffler AE, Dror RO, Shaw DE. Mechanism of voltage gating in potassium channels. Science. 2012;336:229–233. doi: 10.1126/science.1216533. [DOI] [PubMed] [Google Scholar]
- 16.Kim I, Warshel A. Coarse-grained simulations of the gating current in the voltage-activated Kv1. 2 channel. Proc Natl Acad Sci U S A. 2014;111:2128–2133. doi: 10.1073/pnas.1324014111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dryga A, Chakrabarty S, Vicatos S, Warshel A. Realistic simulation of the activation of voltage-gated ion channels. Proc Natl Acad Sci U S A. 2012;109:3335–3340. doi: 10.1073/pnas.1121094109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dryga A, Chakrabarty S, Vicatos S, Warshel A. Coarse grained model for exploring voltage dependent ion channels. Biochim Biophys Acta, Biomembr. 2012;1818:303–317. doi: 10.1016/j.bbamem.2011.07.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kim I, Chakrabarty S, Brzezinski P, Warshel A. Modeling gating charge and voltage changes in response to charge separation in membrane proteins. Proc Natl Acad Sci U S A. 2014;111:11353–11358. doi: 10.1073/pnas.1411573111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kim I, Warshel A. Equilibrium Fluctuation Relations for Voltage Coupling in Membrane Proteins. Biochim Biophys Acta, Biomembr. 2015;1848:2985–2997. doi: 10.1016/j.bbamem.2015.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bennett CH. Efficient estimation of free energy differences from Monte Carlo data. J Comput Phys. 1976;22:245–268. [Google Scholar]
- 22.Crooks GE. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys Rev E: Stat Phys, Plasmas, Fluids, Relat Interdiscip Top. 1999;60:2721. doi: 10.1103/physreve.60.2721. [DOI] [PubMed] [Google Scholar]
- 23.Kim I, Allen TW. Bennett’s acceptance ratio and histogram analysis methods enhanced by umbrella sampling along a reaction coordinate in configurational space. J Chem Phys. 2012;136:164103. doi: 10.1063/1.3701766. [DOI] [PubMed] [Google Scholar]
- 24.Marconi UMB, Puglisi A, Rondoni L, Vulpiani A. Fluctuation–dissipation: response theory in statistical physics. Phys Rep. 2008;461:111–195. [Google Scholar]
- 25.Lacroix JJ, Hyde HC, Campos FV, Bezanilla F. Moving gating charges through the gating pore in a Kv channel voltage sensor. Proc Natl Acad Sci U S A. 2014;111:E1950–E1959. doi: 10.1073/pnas.1406161111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Li Q, Wanderling S, Paduch M, Medovoy D, Singharoy A, McGreevy R, Villalba-Galea CA, Hulse RE, Roux B, Schulten K. Structural mechanism of voltage-dependent gating in an isolated voltage-sensing domain. Nat Struct Mol Biol. 2014;21:244–252. doi: 10.1038/nsmb.2768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sigworth FJ. Structural biology: Life’s transistors. Nature. 2003;423:21–22. doi: 10.1038/423021a. [DOI] [PubMed] [Google Scholar]
- 28.Destexhe A, Huguenard JR. Nonlinear thermodynamic models of voltage-dependent currents. J Comput Neurosci. 2000;9:259–270. doi: 10.1023/a:1026535704537. [DOI] [PubMed] [Google Scholar]
- 29.Schmid G, Goychuk I, Hänggi P. Capacitance fluctuations causing channel noise reduction in stochastic Hodgkin–Huxley systems. Phys Biol. 2006;3:248. doi: 10.1088/1478-3975/3/4/002. [DOI] [PubMed] [Google Scholar]
- 30.Qian H, Zhang XJ, Qian M. Stochastic dynamics of electrical membrane with voltage-dependent ion channel fluctuations. EPL (Europhysics Letters) 2014;106:10002. [Google Scholar]
- 31.Vorobyov I, Kim I, Chu ZT, Warshel A. Refining the treatment of membrane proteins by coarse-grained models. Proteins: Struct, Funct Genet. 2016;84:92–117. doi: 10.1002/prot.24958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Vicatos S, Rychkova A, Mukherjee S, Warshel A. An effective Coarse-grained model for biological simulations: Recent refinements and validations. Proteins: Struct, Funct Genet. 2014;82:1168–1185. doi: 10.1002/prot.24482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hill TL, Chen YD. On the Theory of Ion Transport Across the Nerve Membrane, VI. Free Energy and Activation Free Energies of Conformational Change. Proc Natl Acad Sci U S A. 1972;69:1723–1726. doi: 10.1073/pnas.69.7.1723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Stevens C. Interactions between intrinsic membrane protein and electric field. An approach to studying nerve excitability. Biophys J. 1978;22:295. doi: 10.1016/S0006-3495(78)85490-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Läuger P. Transport noise in membranes. Current and voltage fluctuations at equilibrium. Biochim Biophys Acta, Biomembr. 1978;507:337–349. doi: 10.1016/0005-2736(78)90427-3. [DOI] [PubMed] [Google Scholar]
- 36.Nonner W, Peyser A, Gillespie D, Eisenberg B. Relating microscopic charge movement to macroscopic currents: the Ramo-Shockley theorem applied to ion channels. Biophys J. 2004;87:3716–3722. doi: 10.1529/biophysj.104.047548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Tao X, Lee A, Limapichat W, Dougherty DA, MacKinnon R. A gating charge transfer center in voltage sensors. Science. 2010;328:67–73. doi: 10.1126/science.1185954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Chowdhury S, Chanda B. Estimating the voltage-dependent free energy change of ion channels using the median voltage for activation. J Gen Physiol. 2012;139:3–17. doi: 10.1085/jgp.201110722. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Tsien R, Noble D. A transition state theory approach to the kinetics of conductance changes in excitable membranes. J Membr Biol. 1969;1:248–273. doi: 10.1007/BF01869785. [DOI] [PubMed] [Google Scholar]
- 41.Lacroix JJ, Bezanilla F. Tuning the voltage-sensor motion with a single residue. Biophys J. 2012;103:L23–L25. doi: 10.1016/j.bpj.2012.06.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Thompson AN, Kim I, Panosian TD, Iverson TM, Allen TW, Nimigean CM. Mechanism of potassium-channel selectivity revealed by Na+ and Li+ binding sites within the KcsA pore. Nat Struct Mol Biol. 2009;16:1317–1324. doi: 10.1038/nsmb.1703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Volkán-Kacsó S, Marcus RA. Theory for rates, equilibrium constants, and Brønsted slopes in F1-ATPase single molecule imaging experiments. Proc Natl Acad Sci U S A. 2015;112:14230–14235. doi: 10.1073/pnas.1518489112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Läuger P. Electrogenic ion pumps. Vol. 5 Sinauer Associates; Sunderland: 1991. [Google Scholar]
- 45.Frenkel D, Smit B. Understanding molecular simulation: from algorithms to applications. Vol. 1 Academic Press; 2001. [Google Scholar]
- 46.Jarzynski C. Nonequilibrium equality for free energy differences. Phys Rev Lett. 1997;78:2690. [Google Scholar]
- 47.Crooks GE. Nonequilibrium measurements of free energy differences for microscopically reversible Markovian systems. J Stat Phys. 1998;90:1481–1487. [Google Scholar]
- 48.Evans DJ, Cohen E, Morriss G. Probability of second law violations in shearing steady states. Phys Rev Lett. 1993;71:2401. doi: 10.1103/PhysRevLett.71.2401. [DOI] [PubMed] [Google Scholar]
- 49.Evans DJ, Searles DJ. Equilibrium microstates which generate second law violating steady states. Phys Rev E: Stat Phys, Plasmas, Fluids, Relat Interdiscip Top. 1994;50:1645. doi: 10.1103/physreve.50.1645. [DOI] [PubMed] [Google Scholar]
- 50.Gallavotti G, Cohen E. Dynamical ensembles in non-equilibrium statistical mechanics. Phys Rev Lett. 1995;74:2694. doi: 10.1103/PhysRevLett.74.2694. [DOI] [PubMed] [Google Scholar]
- 51.Jarzynski C. Hamiltonian derivation of a detailed fluctuation theorem. J Stat Phys. 2000;98:77–102. [Google Scholar]
- 52.Kim I, Allen TW. On the selective ion binding hypothesis for potassium channels. Proc Natl Acad Sci U S A. 2011;108:17963–17968. doi: 10.1073/pnas.1110735108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Johnson JB. Thermal agitation of electricity in conductors. Phys Rev. 1928;32:97. [Google Scholar]
- 54.Nyquist H. Thermal agitation of electric charge in conductors. Phys Rev. 1928;32:110. [Google Scholar]
- 55.Stevens CF. Inferences about membrane properties from electrical noise measurements. Biophys J. 1972;12:1028. doi: 10.1016/S0006-3495(72)86141-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Limmer DT, Merlet C, Salanne M, Chandler D, Madden PA, Van Roij R, Rotenberg B. Charge fluctuations in nanoscale capacitors. Phys Rev Lett. 2013;111:106102. doi: 10.1103/PhysRevLett.111.106102. [DOI] [PubMed] [Google Scholar]
- 57.Goychuk I, Hänggi P. Ion channel gating: a first-passage time analysis of the Kramers type. Proc Natl Acad Sci U S A. 2002;99:3552–3556. doi: 10.1073/pnas.052015699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Schoppa N, Sigworth F. Activation of Shaker potassium channels I. Characterization of voltage-dependent transitions. J Gen Physiol. 1998;111:271–294. doi: 10.1085/jgp.111.2.271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Bezanilla F, Perozo E, Stefani E. Gating of Shaker K+ channels: II. The components of gating currents and a model of channel activation. Biophys J. 1994;66:1011. doi: 10.1016/S0006-3495(94)80882-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Zheng J, Trudeau MC. Handbook of ion channels. CRC Press; 2015. [Google Scholar]
- 61.Van Kampen N. Thermal fluctuations in nonlinear systems. J Math Phys. 1963;4:190–194. [Google Scholar]
- 62.Nakamura S, Yamauchi Y, Hashisaka M, Chida K, Kobayashi K, Ono T, Leturcq R, Ensslin K, Saito K, Utsumi Y. Nonequilibrium fluctuation relations in a quantum coherent conductor. Phys Rev Lett. 2010;104:080602. doi: 10.1103/PhysRevLett.104.080602. [DOI] [PubMed] [Google Scholar]
- 63.King G, Lee FS, Warshel A. Microscopic simulations of macroscopic dielectric constants of solvated proteins. J Chem Phys. 1991;95:4366–4377. [Google Scholar]
- 64.Chanda B, Kwame Asamoah O, Blunck R, Roux B, Bezanilla F. Gating charge displacement in voltage-gated ion channels involves limited transmembrane movement. Nature. 2005;436:852–856. doi: 10.1038/nature03888. [DOI] [PubMed] [Google Scholar]
- 65.Lee FS, Chu ZT, Bolger MB, Warshel A. Calculations of antibody-antigen interactions: microscopic and semi-microscopic evaluation of the free energies of binding of phosphorylcholine analogs to McPC603. Protein Eng, Des Sel. 1992;5:215–228. doi: 10.1093/protein/5.3.215. [DOI] [PubMed] [Google Scholar]
- 66.Warshel A, Parson WW. Computer simulations of electron-transfer reactions in solution and in photosynthetic reaction centers. Annu Rev Phys Chem. 1991;42:279–309. doi: 10.1146/annurev.pc.42.100191.001431. [DOI] [PubMed] [Google Scholar]
- 67.Kretchmer JS, Miller TF., III Direct simulation of proton-coupled electron transfer across multiple regimes. J Chem Phys. 2013;138:134109. doi: 10.1063/1.4797462. [DOI] [PubMed] [Google Scholar]
- 68.Läuger P. Thermodynamic and kinetic properties of electrogenic ion pumps. Biochim Biophys Acta, Rev Biomembr. 1984;779:307–341. doi: 10.1016/0304-4157(84)90015-7. [DOI] [PubMed] [Google Scholar]
- 69.Marcus RA. Theoretical relations among rate constants, barriers, and Brønsted slopes of chemical reactions. J Phys Chem. 1968;72:891–899. [Google Scholar]
- 70.Hwang JK, King G, Creighton S, Warshel A. Simulation of free energy relationships and dynamics of SN2 reactions in aqueous solution. J Am Chem Soc. 1988;110:5297–5311. [Google Scholar]
- 71.Rosta E, Warshel A. Origin of Linear Free Energy Relationships: Exploring the Nature of the Off-Diagonal Coupling Elements in SN2 Reactions. J Chem Theory Comput. 2012;8:3574–3585. doi: 10.1021/ct2009329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Hammett LP. Some Relations between Reaction Rates and Equilibrium Constants. Chem Rev. 1935;17:125–136. [Google Scholar]
- 73.Leatherbarrow RJ, Fersht AR, Winter G. Transition-state stabilization in the mechanism of tyrosyl-tRNA synthetase revealed by protein engineering. Proc Natl Acad Sci U S A. 1985;82:7840–7844. doi: 10.1073/pnas.82.23.7840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Åqvist J, Warshel A. Simulation of enzyme reactions using valence bond force fields and other hybrid quantum/classical approaches. Chem Rev. 1993;93:2523–2544. [Google Scholar]
- 75.Warshel A, Schweins T, Fothergill M. Linear free energy relationships in enzymes. Theoretical analysis of the reaction of tyrosyl-tRNA synthetase. J Am Chem Soc. 1994;116:8437–8442. [Google Scholar]
- 76.Schweins T, Warshel A. Mechanistic analysis of the observed linear free energy relationships in p21ras and related systems. Biochemistry. 1996;35:14232–14243. doi: 10.1021/bi961119g. [DOI] [PubMed] [Google Scholar]
- 77.Lomize MA, Lomize AL, Pogozheva ID, Mosberg HI. OPM: orientations of proteins in membranes database. Bioinformatics. 2006;22:623–625. doi: 10.1093/bioinformatics/btk023. [DOI] [PubMed] [Google Scholar]
- 78.Wu EL, Cheng X, Jo S, Rui H, Song KC, Dávila-Contreras EM, Qi Y, Lee J, Monje-Galvan V, Venable RM. CHARMM-GUI Membrane Builder toward realistic biological membrane simulations. J Comput Chem. 2014;35:1997–2004. doi: 10.1002/jcc.23702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Brooks BR, Brooks CL, MacKerell AD, Nilsson L, Petrella RJ, Roux B, Won Y, Archontis G, Bartels C, Boresch S. CHARMM: the biomolecular simulation program. J Comput Chem. 2009;30:1545–1614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Lee FS, Chu ZT, Warshel A. Microscopic and semimicroscopic calculations of electrostatic energies in proteins by the POLARIS and ENZYMIX programs. J Comput Chem. 1993;14:161–185. [Google Scholar]
- 81.O’Donnell C, van Rossum MC. Systematic analysis of the contributions of stochastic voltage gated channels to neuronal noise. Frontiers in computational neuroscience. 2014;8:00105. doi: 10.3389/fncom.2014.00105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Huang Y, Liang J, Chen Y. An Overview of the Applications of Graphene-Based Materials in Supercapacitors. Small. 2012;8:1805–1834. doi: 10.1002/smll.201102635. [DOI] [PubMed] [Google Scholar]
- 83.Rosenblatt S, Yaish Y, Park J, Gore J, Sazonova V, McEuen PL. High performance electrolyte gated carbon nanotube transistors. Nano Lett. 2002;2:869–872. [Google Scholar]
- 84.Warshel A, Weiss RM. An empirical valence bond approach for comparing reactions in solutions and in enzymes. J Am Chem Soc. 1980;102:6218–6226. [Google Scholar]