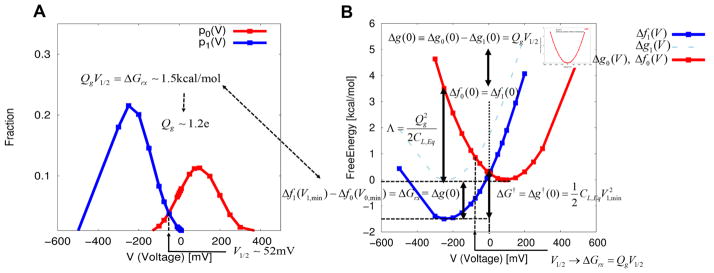
Figure 3.

Illustration of the fundamental free energy relation of the first kind of eq 13 (i.e., the work-fluctuation relation of eq 19) that yield the gating charge, the half voltage, and the equilibrium free energy difference between the resting and the activated states (equivalently, a chemical component of free energy change). An application of the linear response approximation to the membrane/protein/electrolyte system yields the electrolyte-based capacitor-like voltage dependent free energies and new expressions for the reorganization energy and the free energy barrier of voltage activation, in an analogous way with those from the Marcus theory of electron transfer. (A) Probability densities of finding each of the resting and activated state at different external voltages. These probabilities were obtained from the CG energetics using P_λ(V) ∝ exp(−Δf_λ(V)).The intersection of two probabilities yields the half voltage (−V_1/2) of 51. 90 mV at which the resting and activated states are equally probable. Notice that we have a minus sign for the real half voltage, as discussed in details in section III. Together with the equilibrium free energy difference of 1.45 kcal/mol, the formula of eq 29 yields a gating charge of ~1.2e. (B) Corresponding voltage dependent free energies reconstructed from the probabilities of part A using eq 23. The equilibrium free energy difference between the activated and resting states is shown to be equal to the chemical component of free energy change, whose relationship is summarized by eq 28. Notice that the equilibrium free energy difference is obtained by shifting the reference function of Δg₁(V) in such a way that two free energy functions (Δf_λ(V){λ = 0,1}) intersect at zero voltage eq 24, while the fundamental free energy relation of first kind of eq 13 (i.e., the work-fluctuation relation of eq 19) offers an alternative means to evaluate the equilibrium free energy difference. The voltage dependent free energy of Δf₀(V) is reduced to the simple free energy of charging membrane capacitor of eq 31 in the absence of protein charges within the membrane, as shown in the inset.