Abstract
Constraint-based reconstruction and analysis (COBRA) modeling results can be difficult to interpret given the large numbers of reactions in genome-scale models. While paths in metabolic networks can be found, existing methods are not easily combined with constraint-based approaches. To address this limitation, two tools (MapMaker and PathTracer) were developed to find paths (including cycles) between metabolites, where each step transfers carbon from reactant to product. MapMaker predicts carbon transfer maps (CTMs) between metabolites using only information on molecular formulae and reaction stoichiometry, effectively determining which reactants and products share carbon atoms. MapMaker correctly assigned CTMs for over 97% of the 2,251 reactions in an Escherichia coli metabolic model (iJO1366). Using CTMs as inputs, PathTracer finds paths between two metabolites. PathTracer was applied to iJO1366 to investigate the importance of using CTMs and COBRA constraints when enumerating paths, to find active and high flux paths in flux balance analysis (FBA) solutions, to identify paths for putrescine utilization, and to elucidate a potential CO2 fixation pathway in E. coli. These results illustrate how MapMaker and PathTracer can be used in combination with constraint-based models to identify feasible, active, and high flux paths between metabolites.
Keywords: carbon flux, carbon transfer maps (CTMs), flux balance analysis (FBA), metabolic pathway, parsimonious FBA
1 INTRODUCTION
Genome-scale constraint-based metabolic models are powerful tools that predict metabolic fluxes and cellular phenotypes [1], and guide metabolic engineering strategies [2]. While constraint-based reconstruction and analysis (COBRA) methods are useful [3], interpreting their results can be difficult since there are typically hundreds of active fluxes in a solution. The large number of non-zero fluxes makes it difficult to follow where the fluxes are going in the network, since COBRA solutions (which are vectors of flux values) lack details on the metabolic connections between the fluxes. Projecting flux distributions onto metabolic pathway maps can be helpful; however, pathway maps are either generic (with extra or missing reactions compared to a model) or are model-specific and time-consuming to construct. Even if pathway maps exist, it can still be difficult to track carbon flux across them since reactions used to connect two distant metabolites might be shown on different maps. Without a map, one needs to manually look up an active reaction, find its products, and then see what active reactions consume these products to find the next reaction in a path. Thus, general systematic methods are needed to help easily interpret COBRA results. One possible approach is to identify relevant metabolic pathways through which carbon travels.
Prior research has been done to find paths in metabolic networks. Many web-based services can enumerate paths between two metabolites [4-7]; however, the calculations and networks are pre-defined preventing users from making reaction network modifications (e.g., adding/removing/changing reactions) or performing additional tasks (e.g., incorporating flux data or mass-balance constraints). Alternatively, graph-based algorithms can be run on user-specified networks to find paths [8-13]; however, these graph-based methods cannot check whether a path can be mass balanced [14] and cannot be directly integrated with existing COBRA methods. Optimization-based methods can also find paths or cycles in metabolic networks. Linear programming and integer programming methods have been used to find shortest paths or cycles in metabolic networks [15, 16], but these methods did not include mass balance constraints and were not integrated with COBRA models. Another limitation is that in many graph- and optimization-based path analyses, all reactants of a reaction are mapped to all products irrespective of whether atoms (e.g., carbon) are shared between metabolites. As a result, the identified paths might not be biochemically meaningful (e.g., mapping glucose to ADP to pyruvate yields a two step path between glucose and pyruvate). While removing highly connected metabolites (e.g., NAD(P)H and ATP) from the networks prevents some incorrect paths from being found [12], other incorrect paths may still exist and correct paths may be eliminated (e.g., conversion of NADH to NADPH).
To overcome these limitations, Pey and colleagues developed mixed integer linear programming (MILP) approaches that use carbon or carbon atom mappings between metabolites to identify mass-balanced paths [14, 17]. These MILP approaches (and most other approaches) prevent revisiting nodes or edges, and as a consequence, internal cycles are prevented or ignored. While this may be sensible when finding paths between a carbon source and secreted product, discovering cycles and their contribution to metabolism can be critical to understanding metabolic and cellular behaviors. Additionally, the focus of previous efforts has been to find shortest paths between metabolites in a network. Even though these shortest paths may be mass-balanced, they still might not be actively used in COBRA solutions.
We sought to develop methods that could help interpret COBRA results by identifying mass-balanced paths that are actively used in COBRA solutions based on carbon mappings between metabolites. Two methods were developed to predict carbon transfer between reactant and products by metabolic reactions, and to identify paths actively used in genome-scale flux distributions. As described here, this approach which can be directly or sequentially combined with flux balance analysis (FBA, a popular constraint-based modeling approach [1]) or related techniques. This new approach relies on two new tools, MapMaker and PathTracer, which:
Predict carbon transfer between reactants and products: Given reactions and metabolite molecular formula, MapMaker determines all elemental transfers, where each elemental transfer is the number of element atoms in a given reactant that is transferred to given product by a particular reaction. Once a set of elemental transfers for a reaction are found, the carbon transfers are used to create mappings between reactants and products. These carbon transfer maps (CTMs) define the edges (or arcs) that can be traversed to generate paths.
Enumerate paths between two metabolites: A second algorithm, PathTracer, uses MapMaker’s carbon transfer maps for all (or a subset) of reactions, to solve a network flow problem [18]. Given the set of edges as an input, PathTracer finds the shortest, active, most active, or all possible path(s) between two metabolites.
Together, MapMaker and PathTracer can enumerate all possible mass-balanced paths between two metabolites, track carbon flow in a FBA predicted flux distribution, and find metabolite cycles. This allows one to evaluate a genome-scale flux distribution with hundreds of active reactions, and quickly identify how one metabolite is being converted into another. This is useful for finding out which path(s) are being used to make or consume a metabolite (e.g., how pyruvate is made from glucose), which may combine or deviate from canonical biochemical pathways. These two algorithms were applied to the most recent Escherichia coli genome-scale metabolic model [19]. PathTracer and FBA were combined to discover feasible pathways (i.e., pathways that can satisfy COBRA constraints) to convert putrescine into glutamate (a biomass component) and a new CO2 fixation pathway in E. coli. This work shows how an integrated approach can dramatically reduce the paths between metabolites to those that are feasible, active, or most active in constraint-based model predictions.
2 MATERIALS AND METHODS
MapMaker and PathTracer were developed to identify paths between metabolites and to help interpret FBA [1] results. MapMaker uses molecular formulae for a reaction’s reactants and products to predict elemental transfers and CTMs, the latter of which indicate whether a reactant and product share carbon. From MapMaker CTMs (or other metabolite maps), PathTracer enumerates paths between two metabolites or the same metabolite (i.e., cycles).
2.1 MapMaker
MapMaker identifies elemental transfers between reactants and products, from which CTMs are extracted. These CTMs indicate which reactants provide carbon to which products when a reaction occurs. These CTMs differ from atom mapping and bond element matrices, since CTMs do not have any information about which carbon atoms are mapped to each other in a reactant-product pair. Instead, CTMs only indicate that at least one carbon atom is shared by the pair, but the CTMs do not indicate the location of that carbon atom in the reactant/product molecules. MapMaker is a heuristic approach that finds a set of elemental transfers that reduces the transfer of atoms in a reactant to multiple products. MapMaker identifies elemental transfers by minimizing the number of overall transfers (which indicate if a reactant transfers any element to a product), minimizing the number of elemental transfers (which indicate how many different types of elements are transferred between a reactant and product), and maximizing the overall transfer scores associated with each reactant (where the overall transfer scores are based on the numbers and types of elements transferred between a reactant and product).
To determine elemental transfers, MapMaker maximizes the following objective (Eq. 1) for each reaction (j) individually:
| (1) |
where mrp and qrp are the highest and second highest overall transfer scores based on the types of elements and numbers of each element transferred from a reactant (r) to a product (p). R and P are the sets of reactants and products, respectively, that are involved in reaction, j. γerp is a binary variable that has a value of 1 if an element, e, has been transferred from r to p. Ωrp is a binary variable that has a value of 1 if an overall transfer occurs (i.e. whether any elements have been transferred) between r and p. E is the set of all elements in a molecular formula (e.g., C, N, P, S, O) except hydrogen (H).
MapMaker’s elemental transfers must conserve all elements except for hydrogen (Eq. 2 and 3).
| (2) |
| (3) |
where the elemental transfer, δerp, is a non-negative variable representing the number of atoms of element, e, that are transferred from r to p. Sij is the stoichiometric coefficient for metabolite (i) in reaction (j), a minus sign is used in Eq. 3 because the stoichiometric coefficients for reactants (Srj) are negative. MFie is a parameter derived from the molecular formula indicating the number of atoms of element, e, contained in metabolite, i. The metabolite (i) can be a reactant (r) or product (p).
MapMaker uses two types of binary penalty variables, γ and Ω, in the objective function (Eq. 1), and Eq. 4 and 5 ensure that γerp and Ωrp are 1 if elements are transferred (i.e., δerp > 0) from r to p:
| (4) |
| (5) |
An overall transfer describes the numbers of all elements that are transferred between a reactant (r) and product (p). MapMaker gives each overall transfer a score based on the number of atoms transferred (δerp) and the weighting factor we for each element type. For a group of elements represented as ‘R’ in the molecular formula wR was set to 40; while the weighting for N, O and P (wN, wO, wP) was set to 0.4 and the weighting for all other elements (except H) was 1. These weights were chosen so it should be easier to transfer a N, O or P atom to another compound than a C atom. The highest and second highest (if one exists) overall transfer scores associated with a given reactant are defined as mrp and qrp, respectively. The mrp and qrp variables are constrained by Eq. 6 to 13.
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
Here, xrp and yrp are binary indicator variables used to select the highest and second highest scoring overall transfer from reactant, r. Eq. 6 and Eq. 9 set upper bounds for the overall transfer scores based on the number of each type of element transferred to a product (δerp) and the weight for each element (we). Eqs. 7, 8, 10, 11 and 12 ensure that only one highest (mrp) and second highest (qrp) overall transfer score for each reactant can contribute (i.e. being non-zero) to the objective function (Eq. 1). The parameter Zr represents the largest score that could be achieved by transferring all elements from a given reactant, r, and is determined by Eq. 13.
| (13) |
Eq. 6 to 12 ensure at most one mrp and at most one qrp, can be non-zero for a given reactant, r, participating in reaction, j. Consequently, each reactant’s highest priority overall transfer score (mrp) is scaled the most in MapMaker’s objective function (Eq. 1). For reactants’ with multiple overall transfers, the second priority overall transfer scores (qrp) are also included in the objective, but are scaled by a smaller amount. Since the weighting for transferring carbon atoms is higher than N, O, P, and S atoms, and the highest overall transfer score (mrp) contributes more towards the overall objective function (Eq. 1), then MapMaker prefers solutions where carbon from a reactant is transferred to fewer products. Overall transfer scores for any additional overall transfers are not included in the objective function. MapMaker solutions for some reactions are sensitive to the parameter values used in Eq. 1 (e.g., weighting the third term by 50 instead of 1 introduces ~6 additional erroneous carbon transfer maps). The parameter values chosen resulted in more accurate carbon transfer maps (CTMs) for the reactions in iJO1366. MapMaker was implemented in GAMS (General Algebraic Modeling Systems) and solved using CPLEX (Intel Core i7 920 @ 2.67 GHz with 12 GB of memory running on Windows 10), with runtimes of around 0.02 seconds per reaction analyzed.
2.2 General Reaction-Based Maps and MapMaker CTMs
The CTMs correspond to reactants (r) and products (p) where γCrp=1. To investigate the sensitivity of PathTracer to other mappings (or connections) between metabolites, general reaction-based maps were used, such that each reactant is mapped to all products of a given reaction regardless of whether a carbon transfer has occurred. The CTMs generated by MapMaker are a subset of these reaction-based maps. In some cases the general reaction-based maps were further refined by removing highly connected metabolites (e.g., ATP and NADH) using Eq. 23. Unless indicated otherwise, PathTracer was run using MapMaker CTMs.
2.3 PathTracer Algorithm
From the metabolite maps (either reaction-based or MapMaker CTMs), a network flow problem can be formulated to (1) enumerate all possible paths from a starting metabolite (StartNode) to an ending metabolite (EndNode), or (2) determine the shortest or most active path between two metabolites utilized by an FBA solution (see section 2.4). PathTracer uses an objective function (Eq. 14 or Eq. 26) to select a path that satisfies required constraints (Eq. 16 to 21, ensuring flow into a metabolite node equals flow out of a node), and optional constraints (Eq. 22 to 30, limiting the number of times a metabolite node or reaction can be used in a path). To find the shortest path(s), the following objective function is used:
| (14) |
where D is an ordered set of depths from 1 to ∣D∣ (in this work, ∣D∣ was set to 30), and Sinkd are binary variables used to remove flow (if value is 1) from the ending metabolite node at different depths, d. In Eq. 14, the first term was weighted more than the second so that PathTracer finds a path instead of not returning a path. If a path is found, the first term has a value of 10 · ∣D∣ and the second term has a value equal to the path length. As long as the weighting on the first term is greater than ∣D∣, then PathTracer will return a path even it is long. This objective function was used instead of forcing PathTracer to find a path (by setting and minimizing instead of Eq. 14) so that the PathTracer MILP was always feasible.
A network is created whose nodes (indicated as n or i) are connected by edges based on metabolite maps. Sink and source edges are added to the starting and ending metabolite, respectively. Flow is conserved across each node at different depths (d) using constraints (Eq. 15 to 20):
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
| (20) |
Map is the set of all mappings from reactants to products via reactions (j). Note, that Map can include all reactions, reactions found by flux variability analysis (FVA [20]) that satisfy COBRA constraints, or a subset of reactions which are predicted by FBA or pFBA to be active (see section 2.4 for more details). The order of the Map subindices correspond to reactant, reaction, and product in the forward direction of the reaction. For, example, Mapnji indicates that node n is mapped in the forward direction of reaction j to node i, and Mapijn indicates that node i is mapped in the forward direction of j to node n. d is the depth (i.e., the distance traversed from the starting metabolite to metabolite n). Binary variables a and arev indicate flow (if value is 1) between metabolite nodes in the forward or backward direction of a reaction, respectively. The arev variables only exist for reversible reactions. The order of the a and arev subindices correspond to reactant, reaction, product, and depth. For example, anjid =1 indicates flow from node n by reaction j to node i at depth d and indicates flow from node i using reaction j (in the backward direction) to node n at depth d. Source is a binary variable associated with the starting metabolite, which takes a value of 1 if a path is found from this starting metabolite to the ending metabolite.
In addition to the required constraints (Eq. 15 to 20), the following optional constraints can prevent a reaction(s) from being used in a path (Eq. 21), prevent all reactions (defined as set J) from being used more than once (Eq. 22), prevent a node(s) from being included in a path (Eq. 23) or prevent all nodes from being used more than once to avoid internal loops (Eq. 24 and 25). In this work, the eliminated set of nodes included: CO2, ACP and CoA (for the putrescine to glutamate analyses); ACP and CoA (for the CO2 fixation simulations); and H, H2O, NAD, NADH, NADP, NADPH, ATP, ADP, AMP, CoA and ACP (when using general reaction-based maps instead of MapMaker CTMs). Integer cuts can also be used to find alternative MapMaker and PathTracer solutions and these cut constraints are described in the Supporting Information.
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
2.4 Integrating FBA (or pFBA) and PathTracer
PathTracer can find paths used in FBA [1], pFBA [21], or FVA [20, 22] solutions by only allowing CTMs of active (i.e., non-zero) fluxes to be used, thereby reducing the number of possible paths. For example, a one-step pFBA solution (see Eq. S1 to S5 in Supporting Information) can be found that maximizes biomass (or metabolite production) and minimizes the total absolute flux through the network. The pFBA or FBA solution is used to reduce the set of maps (Map) considered by PathTracer. PathTracer can then find the shortest active path (using Eq. 14 to 20) or the most active path (using Eq. 26 and 15 to 20) in the pFBA/FBA solution, which also satisfies optional constraints imposed (Eq. 21 to 25). To find the most active path, a new objective function (Eq. 26) is used that scales the flow variables by the inverse of their associated pFBA/FBA predicted non-zero fluxes (vj).
| (26) |
Here λ is a large parameter that helps the objective function favor finding a path over minimizing the some of scaled flow variables, and λ equal to 104 was used in this work. Note that in Eq. 26 the fluxes are parameters instead of variables, since the FBA or pFBA problem is solved first. The first term of Eq. 26 encourages PathTracer to find a path (in this case Σ Sinkd is 1). The second and third terms of Eq. 26 bias the selection of which edges are active by the inverse of the flux values, so that edges associated with high fluxes are penalized less in the objective. The large λ value ensures that finding a path is favored over returning a no path solution (to avoid using edges associated with reactions with low flux). For models with smaller fluxes than iJO1366, λ may need to be increased (which would be evident if no paths were returned by PathTracer), or instead PathTracer can be run with an additional constraint () so that the first term can be removed from the objective function (Eq. 26).
This first approach is useful to find which paths are actively being used in a FBA or pFBA solution. However, other flux distributions exist, and it is often desirable to identify any or all paths between two metabolites (not just a path in a single FBA or pFBA solution). To ensure PathTracer proposes a feasible path (i.e., satisfies steady-state mass balance, enzyme capacity, and reversibility constraints), the COBRA constraints (Eq. 27 to 32) can be directly included in PathTracer.
| (27) |
| (28) |
| (29) |
| (30) |
| (31) |
| (32) |
Here, Inonbio is the set of all non-biomass metabolites and Ibio is the set of metabolites in the Biomass reaction. Non-negative fluxes through individual sinks () for biomass components were used instead of the biomass reaction in mass balances (Eq. 28) to reduce solver issues associated with poorly-scaled models. The binary variables, Forwardj and Reversej, indicate whether a path uses the reaction in the forward or reverse direction, respectively. The upper and lower limits for each flux (vj) are and , respectively. Eq. 29 to 32 ensure that if a reaction is used in a path then the flux is greater than φ (if the reaction is used in the path in the forward direction) or less than φ (if the reaction is used in the reverse direction). Thus, φ is the minimum flux a reaction needs to carry to be allowed in a path. φ was set between 10−2 and 10−3 (depending on how ill-conditioned the equations were) so that only higher flux paths were found. This approach was used to find feasible paths between glucose and all other metabolites. As with MapMaker, PathTracer was implemented in GAMS and solved using CPLEX. When FBA was run as a separate initial problem, it took PathTracer about 1 second to find a path using active fluxes from the FBA solution. When PathTracer and FBA/pFBA were integrated into a single MILP the runtime was around 13 seconds (Intel Core i7 920 @ 2.67 GHz with 12 GB of memory running on Windows 10). In either case, PathTracer was able to find paths within a reasonable timeframe.
3 RESULTS
Two algorithms were developed to predict what elements are transferred from reactants to products in biochemical reactions (MapMaker), and to identify paths between two metabolites where all reaction steps transfer carbon atoms between substrates and products (PathTracer). MapMaker identified which reactants and products share carbon atoms in a genome-scale metabolic network of E. coli [19]. This carbon mapping information was used by PathTracer to investigate shortest path lengths, to elucidate a CO2 fixation pathway, and to identify high flux paths in a genome-scale E. coli model.
3.1 MapMaker: Predicting Elemental Transfers of Reactions
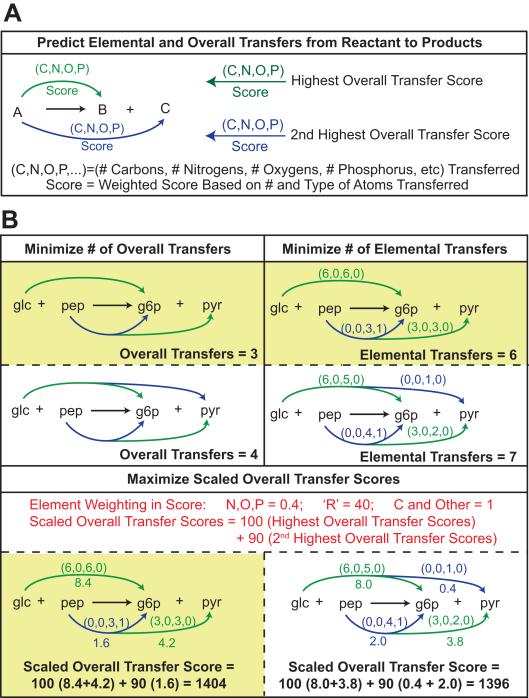
The process of generating a carbon transfer map (CTM) for a given reaction is summarized in Figure 1. As depicted (Figure 1A), MapMaker distributes all non-hydrogen elements in the reactants of a given reaction to products. All reactions analyzed by MapMaker must be elementally-balanced (except for hydrogen). There are numerous ways to distribute elements from multiple reactants to multiple products; consequently, MapMaker is predicated on the principle of Occam’s Razor or maximum parsimony (i.e., the simplest explanation is preferred). Maximum parsimony approaches have been used to refine metabolic and regulatory models [23-25], predict intracellular fluxes [21, 26], and identify metabolic engineering targets [2, 27]. Based on this principle, MapMaker finds all elemental transfers for a given reaction by distributing reactant elements to the fewest number of products. To accomplish this, a multi-component objective function (Figure 1B) is used which:
Minimizes the Number of Overall Transfers: Here an overall transfer is a culmination of all the elemental transfers (e.g., carbon, nitrogen, phosphorous, and oxygen) between a reactant and its product. If no elements are transferred between two metabolites then there is no overall transfer. The number of elements (e.g., two versus one carbon atom) and element types (e.g., carbon and nitrogen elements) transferred from a reactant to a product is not considered in this part of the multicomponent objective function.
Minimizes the Number of Elemental Transfers: Here the number of element types transferred between reactants and products for a given reaction is considered. Again, the number of each type of element transferred does not impact this part of the objective function. Instead, the number of elemental transfers increases when a new type of element is transferred between two compounds.
Maximizes the Scaled Scores for the Overall Transfers: Each overall transfer between a reactant and product is given a score based on the number and type of elements transferred. The highest and second highest scores for each reactant are then scaled in the multicomponent objective function, and collectively contribute the most to its overall value. By maximizing the scaled overall transfer scores, the algorithm tries to assign as many reactant elements as possible to a single product.
The subset of optimal elemental transfers that involve carbon atoms are used to create CTMs from reactants to products, which serve as inputs for the PathTracer algorithm. MapMaker’s elemental transfers do not contain detail about which carbon atom in a reactant becomes which carbon atom in a product. As a result the CTMs only specify that at least one carbon atom is shared between two metabolites, and not which carbon atoms in the two metabolites these correspond to.
Figure 1. Overview of MapMaker Algorithm.
(A) The MapMaker algorithm predicts elemental transfers for a given reaction that conserve elements, except for H. The reaction representing glucose transport is shown as an example. The abbreviations correspond to glucose (glc), phosphoenolpyruvate (pep), glucose-6-phosphate (g6p), and pyruvate (pyr). Each arc (blue or green) connecting two metabolites represents an overall transfer (indicating that elements are transferred from reactant to product). The numbers in parentheses above the overall transfer arcs are the numbers of each type of element that are being transferred. For example, a (2,2,3,1) indicates 2 carbon, 2 nitrogen, 3 oxygen, and 1 phosphorous atoms are being transferred from the reactant to that product. The number below the overall transfer arcs are the corresponding overall transfer scores. MapMaker uses a multi-component objective function that considers number of overall transfers, number of elemental transfers (the number of non-zero entries in the parentheses), and scaled overall transfer scores (B). Yellow boxes indicate MapMaker’s preferred option given two hypothetical scenarios.
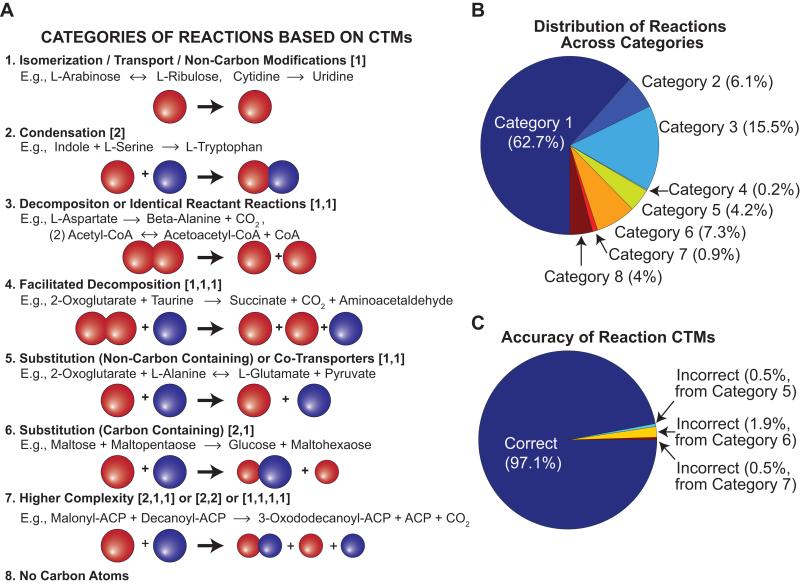
MapMaker was applied to all the reactions (except the biomass reaction) in the E. coli iJO1366 metabolic network [19], resulting in elemental transfers for 2,251 reactions. The resulting CTMs derived from the carbon transfers were checked for accuracy. Reactions were categorized based on how reactants’ carbon atoms were separated and/or combined by a reaction (e.g., a condensation reaction has two CTMs between two reactants and a single product), resulting in 8 reaction categories (Figure 2A). When assigning reactions to a category, CTMs for energy and redox carriers (e.g., ATP, GTP, and NAD(P)H) were ignored, unless they were the only reactants; however, reactions involving energy/redox carriers were then placed in a separate subcategory. Energy/redox carriers were not identified before running MapMaker, but were instead used to distinguish between subcategories in the classification scheme. The number of reactions and accuracy of CTMs in each category (and subcategory) are detailed in Table S1.
Figure 2. Reaction Categories and their Carbon Transfer Map Accuracies.
CTMs generated from MapMaker were used to assign reactions to one of 8 categories (see text for details). Each number in brackets is the number of unique reactants that are mapped (via CTMs) to a given product. For example, [2,1] indicates carbons in the first product come from two reactants and carbons in the second product come from one reactant. Energy and redox carriers were initially ignored when categorizing reactions. Panels B and C show the number of reactions in each category and percent of reactions with correct and incorrect CTMs, respectively.
The first three categories involve reactions with single carbon containing reactants or products, including reactions: with only one reactant and one product with carbon atoms (category 1); where two carbon containing reactants combine into a single product (category 2); where a single carbon compound decomposes into two products (category 3). If no energy/redox carriers are involved in the reactions, then the CTMs for reactions in these three categories are guaranteed to be correct (i.e., no alternative carbon transfer map solution exists). Approximately 83% of the iJO1366 reactions fall into the first three categories (Figure 2B), and the MapMaker CTMs were 100% accurate, irrespective of whether energy/redox carriers were involved in the reactions (which were not guaranteed to be correct). The remaining four categories (categories 4 to 7), which comprise ~13% of iJO1366 reactions, involve mapping multiple carbon containing reactants to multiple carbon containing products (the remaining ~4% of reactions do not involve any organic compounds, category 8). A majority of reactions in categories 4 to 7 transfer a functional group (e.g., amine, CO2, CoA or ACP). Overall, only 66 reactions (~3%) of reactions had incorrect MapMaker CTMs (Figure 2C) and these mostly involved reactions (1) where a functional group (e.g., CoA) was present in two reactants and a separate product, or (2) where reactants and products had similar chemical compositions (see Table S2).
3.2 PathTracer: Tracing Carbon through Metabolic Networks
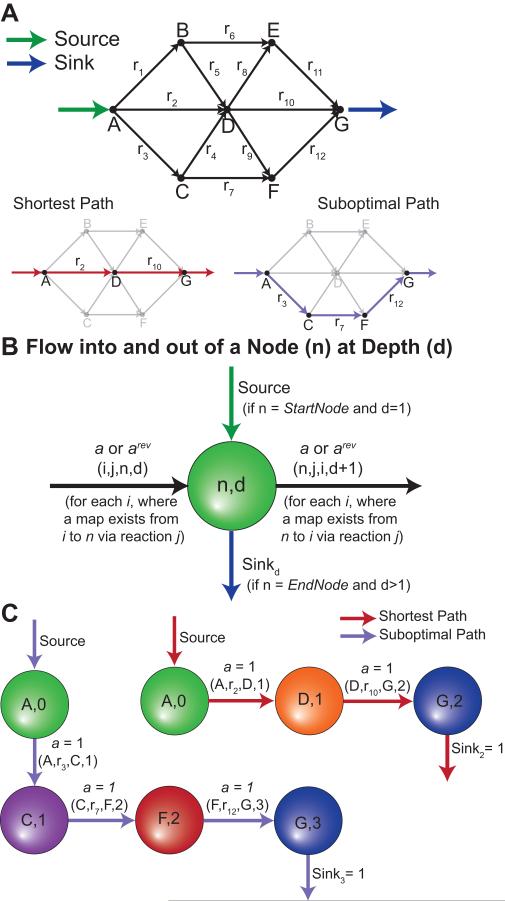
PathTracer uses CTMs to determine paths involving carbon flow between a starting and ending metabolite. PathTracer was first applied to a toy metabolic system to enumerate all paths from metabolite A to metabolite G (Figure 3A). This was accomplished by creating a network of metabolite nodes at a given depth (d) away from the starting node, where the movement across an edge from one node to another increases the depth by one. Each node (n) is connected to other nodes (i) by edges (corresponding to CTMs) between reactions’ reactants (r) and products (p). Most of connections were generated from MapMaker CTMs, but other metabolite maps can be used, including other MapMaker element transfers (e.g., nitrogen transfers) or mappings between all reactants and products (i.e., general reaction-based maps that have been used previously [12, 16, 28]). A source edge is added to the starting metabolite node at the first depth (d=1) and flow is allowed through this source edge into the network (Figure 3B). Sink edges are also added to the nodes corresponding to the ending metabolite for each depth greater than one (d>1). A path can be found between two metabolites by conserving flow across each node (i.e., flow in and out of given node must be equal). The shortest path involves flow through the shallowest (i.e., smallest d) sink edge (Figure 3C). To enumerate other possible paths (Figure 3C), integer cuts can be added to eliminate prior shortest paths. The following sections show how PathTracer can help analyze FBA results and reveal interesting network behaviors in genome-scale metabolic networks.
Figure 3. Illustrative Example for Generating Paths.
(Panel A) PathTracer was applied to a toy network to find all reaction paths from metabolite A to G. (Panel B and C) One source edge (green arrow) was added to the starting metabolite’s first depth node. Sink edges (blue arrows) were added to the ending metabolite’s nodes with depths greater than one. (Panel B) The flow inputs and outputs of a given node (n) at depth (d) are based on source edges, sink edges, connections to other nodes (i) based on metabolite maps (e.g., CTMs). PathTracer balanced flow around each node to determine the shortest reaction path from the source edge to a sink edge (Panel C). Here the red path indicates the shortest possible path between A and G, while the purple path indicates an alternate solution that was found with integer cuts.
3.3 Paths in a Genome-Scale Metabolic Network
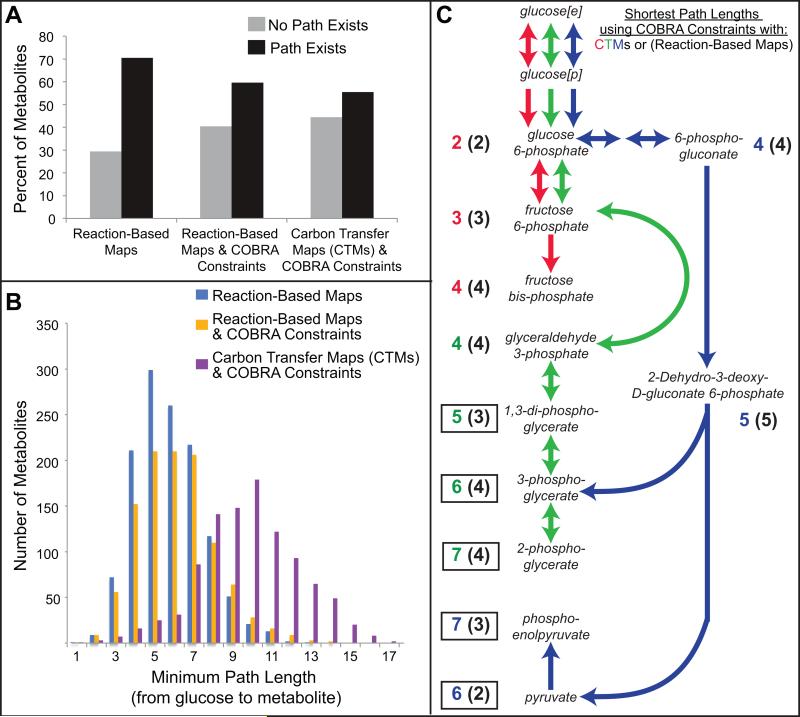
PathTracer was first used to find paths from glucose to every other metabolite in the iJO1366 network. To evaluate the impact of CTMs and mass balances on paths, PathTracer was run using general reaction-based maps (where all reactants were connected to all reactants in a reaction) or CTMs, and with or without COBRA constraints (including steady-state mass balance, enzyme capacity, and reversibility constraints). Imposing COBRA constraints on reaction-based maps dramatically reduced the percent of metabolites with paths from glucose, from 71% to 60% (Figure 4A). Thus, existing approaches that do not consider COBRA constraints will propose paths involving metabolites that cannot be consumed or produced by the network (Figure 4A). Using CTMs to connect metabolites further reduced the set of reachable metabolites from glucose to 55%, suggesting that 5% of metabolites may only be connected to glucose via non-carbon atoms (e.g., nitrogen, oxygen, and phosphorous). Using CTMs also increased the average minimum path length between glucose and all reachable metabolites from ~6 reactions to ~10 reactions (Figure 4B). The shortest paths for glycolytic intermediates differed significantly depending on whether reaction-based maps versus CTMs were used with COBRA constraints (Figure 4C). Even with highly connected metabolites removed (e.g., ATP), the reaction-based maps resulted in a two-step path from extracellular glucose (glc-D[e]) to intracellular pyruvate (pyr): glc-D[e] to glc-D[p] to pyr. This is because the PTS glucose transport reaction (glc-D[p] + pep → g6p + pyr) connects glc-D[p] to pyr in reaction-based maps even though no carbon is exchanged between glucose and pyruvate. Given these results, all subsequent PathTracer analyses used CTMs with COBRA constraints or FBA results to generate feasible paths that satisfy mass balances, reversibility, and enzyme capacity constraints.
Figure 4. Effect of COBRA constraints and CTMs on Shortest Paths.
Shortest paths between glucose and all other metabolites were calculated using either: general reaction-based maps without COBRA constraints, general reaction-based maps with COBRA constraints, or CTMs with COBRA constraints. The COBRA constraints were for aerobic glucose minimal media conditions. General reaction-based maps connected all reactants to all products; however, some highly connected metabolites were eliminated (see methods for details). (A) The percent of metabolites with or without paths from glucose. (B) Histogram of shortest paths lengths for metabolites with paths from glucose. (C) Shortest paths between extracellular glucose and different central metabolic intermediates found using CTMs with COBRA constraints. The numbers reported next to each metabolite indicate the shortest path lengths found using CTMs with COBRA constraints (left) and reaction-based maps with COBRA constraints (right, in parentheses). Boxes highlight where the two calculated path lengths differ. The different colored path length numbers match the colored arrows used in the path. For example, the shortest path to pyruvate using CTMs (with path length of 6, shown in blue) uses reactions shown in blue.
Another algorithm, FOCAL, was previously developed to identify conditions where a chosen reaction would be essential for growth [16]. The NAD-dependent succinate-semialdehyde dehydrogenase reaction (SSALx) was predicted, by an older E. coli model (iJR904 [29]), to be essential for a ΔgabD mutant grown aerobically with putrescine as sole carbon source. Compared to iJR904, iJO1366 includes more reactions to convert putrescine into biomass so SSALx is not predicted to be essential in these conditions for ΔgabD (which lacks the NADP-dependent succinate-semialdehyde dehydrogenase, SSALy). Paths between putrescine and biomass were calculated using PathTracer to see how biomass is produced from putrescine in iJO1366. Since PathTracer found that glutamate was the closest biomass component to putrescine (i.e., glutamate had the shortest path with 8 reactions), glutamate was used as the ending metabolite for all subsequent PathTracer analyses.
PathTracer generated all feasible paths (with d<30) from putrescine to glutamate, and the 15 shortest paths are shown in (Figure S1). Since PathTracer does not use carbon fates (i.e., which reactant carbon atom goes to which product carbon atom), one path involving gamma glutamyl putrescine synthase (GGPTRCS) was incorrect because no carbon atoms go from putrescine to glutamate. All correct paths which did not use SSALx instead used either SSALy or spermidine synthase (SPMS). Thus, SSALy and SPMS would both need to be eliminated to make SSALx essential for growth. The essentiality conditions (removing SSALy and SPMS) can also be found using a bilevel MILP that destroys all paths between two metabolites, eliminating the need to enumerate and inspect all paths (see Supporting Information for details). While PathTracer found no paths involving carbon flow between putrescine and glutamate after SSALx, SSALy, SPMS and GGPTRCS were removed, FBA still predicted growth for this quadruple knockout mutant. The only other carbon available in the FBA simulations was CO2, and in the absence of these four reactions iJO1366 used putrescine as an energy and electron source to fix CO2.
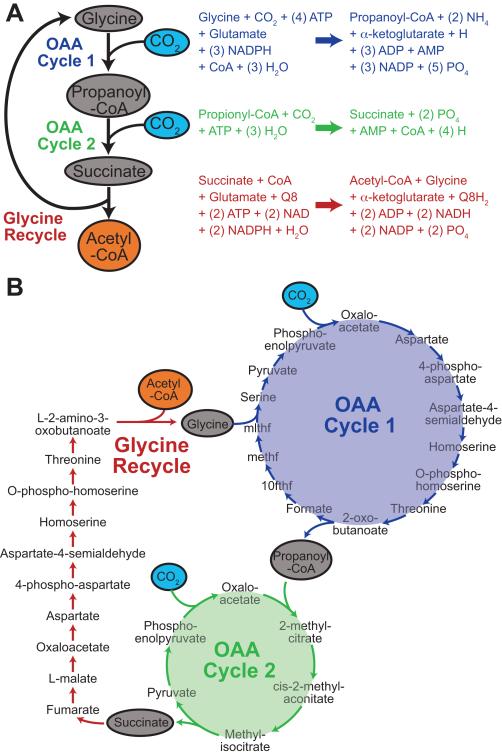
PathTracer was subsequently used to evaluate what paths were being used in the iJO1366 model to enable CO2 fixation, as well as what network changes had occurred between iJR904 and iJO1366 to allow for this new predicted phenotype. All feasible paths (which satisfy COBRA constraints) between CO2 and glutamate were found using PathTracer and only four reactions involved in these paths utilize CO2 — carbamate kinase, carbonic anhydrase, pyruvate oxidoreductase, and phosphoenolpyruvate carboxylase (PPC). Of these four reactions, only PPC was required to produce glutamate from CO2 (as determined by FBA) implying the CO2 fixation pathway involved oxaloacetate (the product of PPC). pFBA was used to predict the set of reactions used to produce glutamate from CO2 and putrescine (and other minimal medium nutrients), after deleting GGPTRCS, SPMS, SSALx and SSALy (to prevent putrescine utilization as a carbon source) and deleting the three non-essential CO2 consuming reactions (carbamate kinase, carbonic anhydrase, and pyruvate oxidoreductase). PathTracer was re-run using only reactions in this pFBA solution to discover paths between CO2 and glutamate involving oxaloacetate cycles. Ten oxaloacetate cycles were found, of which two of them, if combined, produced succinate from glycine and two molecules of CO2 (see Figure 5). Another PathTracer search on this pFBA reaction set found a path from succinate to glycine that also produced acetyl-CoA (Figure 5B). Combined, these three paths resulted in the net generation of acetyl-CoA from ATP, NADPH and CO2. The ATP and NAD(P)H needed to run this CO2 fixation pathway were produced by the degradation of putrescine into 4-aminobutanoate. The acetyl-CoA produced can then be used to make biomass components, including glutamate. While this multi-step approach found linear and cyclic paths involved in CO2 fixation, a modification to PathTracer can also determine in one step a complete set of paths necessary to convert CO2 to glutamate (see Supporting Information, Figure S2, and Tables S3-S12 for details).
Figure 5. CO2 Fixation Pathway in iJO1366.
(A) An overview of the oxaloacetate (OAA) cycles and glycine recycling paths (along with their overall reactions) that when combined allow conversion of two molecules of CO2 into acetyl-CoA. (B). Detailed steps in the OAA cycles and glycine recycling pathway. Abbreviations of tetrahydrofolate derived metabolites (10fthf, methf, mlthf) are consistent with those used in iJO1366.
While putrescine was used to provide the necessary ATP and NAD(P)H for CO2 fixation, any source of NAD(P)H and ATP could be used. A total of 9 ATP equivalents and 5 NAD(P)H molecules were required to convert two CO2 into acetyl-CoA (with 1 ubiquinone being reduced). This CO2 fixation pathway uses more steps and is less efficient energetically than five of the six known CO2 fixation pathways. For example, the dicarboxylate/4-hydroxybutyrate pathway requires 5 ATP equivalents to convert two CO2 into acetyl-CoA [30]. Of the reaction set used by pFBA, only 13 reactions were new or modified in iJO1366 compared to iJR904 (excluding outer membrane transport reactions). Just making the glycine hydroxymethyltransferase (GHMT2) reaction reversible in the iJR904 model allowed iJR904 to fix CO2. The most recent estimate for the standard change in Gibbs free energy for the GHMT2 reaction (ΔR G′0) was 0.05 ± 3.65 kcal/mol [31], indicating this reaction is likely reversible. However, E. coli is not known to fix CO2 physiologically. One reason for this could be due to transcriptional regulation. In the first OAA cycle and glycine recycle (Figure 5B), threonine is an intermediate that is synthesized and then degraded. However, threonine biosynthesis and threonine degradation enzymes are not typically expressed under the same conditions [32, 33]. Additionally, the second OAA cycle uses enzymes involved in propionate degradation that are induced during growth on propionate [34]. For the CO2 fixation path to function, the regulatory network would need to be configured to allow the necessary enzymes to be expressed simultaneously. Compared to other CO2 fixation paths, this potential path is not the most energetically efficient and requires significantly more enzymatic steps to complete. As a result, other pathways might be better to incorporate into E. coli to enable CO2 fixation.
3.4 Finding High Flux Paths
When analyzing FBA or pFBA results, one may be interested in finding the most active path (i.e., the one with the highest flux) used to produce a particular metabolite. By using FBA results to reduce the set of reactions considered by PathTracer, all possible active paths between two metabolites can be enumerated. However, some of these paths may not contribute significant flux between two metabolites. To find the most active path, a modified PathTracer objective function can be used (see Methods) where each individual edge is weighted by the inverse of its FBA predicted flux value. The differences between the shortest and flux-weighted paths can be significant. For example, two paths between glucose and ethanol were found using only active reactions in a pFBA solution by (1) minimizing pathlength or (2) minimizing a flux-weighted objective function (Table 1). The two paths found were significantly different, with the shortest active path using the Entner-Dourdoroff (EDD and EDA) and pyruvate oxidoreductase (POR5) reactions and the flux-weighted path using glycolysis and pyruvate dehydrogenase (PDH). Consequently, while both approaches find feasible and metabolically active paths, the flux-weighted path captures the more dominant metabolic behavior. These high flux paths are useful for knowing which path contributes the most towards metabolite or precursor production, which can be useful when determining whether network modifications are likely to have large or small impacts on flux re-arrangements or whether these are paths are consistent with measured ‘omics’ datasets.
Table 1.
Paths between glucose and ethanol used in an pFBA solution for a mutanta strain grown under glucose anaerobic conditions.
| Shortest Active Path | Flux-Weighted Path | ||||||
|---|---|---|---|---|---|---|---|
|
| |||||||
| Map Fromb | Map Tob | Rxnb | pFBA Fluxc |
Map Fromb | Map Tob | Rxnb | pFBA Fluxc |
|
| |||||||
| glc-D[e] | glc-D[p] | GLCtex | 10 | glc-D[e] | glc-D[p] | GLCtex | 10 |
| glc-D[p] | g6p | GLCptspp | 10 | glc-D[p] | g6p | GLCptspp | 10 |
| g6p | 6pgl | G6PDH2r | 1.9 | g6p | f6p | PGI | 8.1 |
| 6pgl | 6pglc | PGL | 1.9 | f6p | fdp | PFK | 7.7 |
| 6pgc | 2ddg6p | EDD | 1.9 | fdp | g3p | FBA | 7.7 |
| 2ddg6p | pyr | EDA | 1.9 | g3p | 13dpg | GAPD | 17.5 |
| pyr | accoa | POR5 | 0.3 | 13dpg | 3pg | PGK | −17.5 |
| accoa | acald | ACALD | −17.4 | 3pg | 2pg | PGM | −17.2 |
| acald | etoh | ALCD2x | −17.7 | 2pg | pep | ENO | 17.2 |
| etoh | etoh[p] | ETOHtrpp | −17.7 | pep | pyr | PYK | 6.6 |
| etoh[p] | etoh[e] | ETOHtex | −17.7 | pyr | accoa | PDH | 17.8 |
| accoa | acald | ACALD | −17.4 | ||||
| acald | etoh | ALCD2x | −17.7 | ||||
| etoh | etoh[p] | ETOHtrpp | −17.7 | ||||
| etoh[p] | etoh[e] | ETOHtex | −17.7 | ||||
The mutant had the following reactions deleted: ATPS4rpp, DHAPT, D-LACt2pp, GLYCLTt2rpp, L-LACt2rpp.
Metabolite and reaction abbreviations match those used in iJO1366.
Fluxes are reported in units of mmol/gDW/h.
4 DISCUSSION
This work developed a heuristic approach to predict CTMs between metabolites using stoichiometric and molecular formulae information for metabolites participating in a reaction. The approach was highly accurate, with over 97% of reactions in iJO1366 having the correct CTMs. Incorrect CTMs were associated with substitutions or higher complexity reactions (Categories 5-7), indicating the CTMs for reactions of these types (~12% of the reactions in iJO1366) should be validated. MapMaker solutions are sensitive to the parameters used and it is possible further optimization of these parameters or introduction of additional considerations could reduce the error rate. Software exists that identifies functional groups from molecular structures [35], and MapMaker errors could potentially be reduced by taking functional groups into account. MapMaker allows for the rapid and automated identification of metabolites in a reaction that share at least one carbon atom; however, it does not predict the fates (or locations) of individual carbon atoms in substrates and reactants (e.g., the 2nd carbon in the reactant becomes the 1st carbon in the product).
We show that the MapMaker CTMs and COBRA constraints have a significant impact on the number of metabolites with paths from glucose and the shortest paths found using PathTracer. Pey et al. made similar observations for a different E. coli network using a related MILP approach [14]. Since PathTracer does not follow individual carbon atoms it sometimes connects metabolites via paths where carbon is not shared between a starting and ending metabolite. Such an incorrect path was found between putrescine and glutamate, where the carbon in glutamate should come entirely from α-ketoglutarate. The incorrect path generates an intermediate that contains carbon from both putrescine and α-ketoglutarate and since PathTracer does not trace the fate of individual carbon atoms it connects this intermediate to glutamate. Recently, Pey et al. have proposed an approach that uses carbon fate information to track individual carbon atoms through metabolic reactions [17]. This approach correctly finds paths where the starting and ending metabolite (and all intermediates) share carbon atom(s); however, the approach requires carbon atom reaction transitions for all reactions. Future, work could combine Pey et al.’s approach [17] for tracking carbon atoms with constraint-based models to better track the flow of carbon atoms through FBA or pFBA solutions.
While both algorithms proposed by Pey et al. impose mass-balanced constraints [14, 17], they require that any reaction used in a path must be carry a flux greater than 1 and still result in a mass-balanced flux distribution. However, for many FBA solutions most of the fluxes are less than 1 mmol/gDW/h. For example, ~86% of the active fluxes are less than 1 mmol/gDW/h in a pFBA solution for iJO1366 under glucose minimal media aerobic conditions. Paths using these low-flux reactions would not be found if enzyme capacity and reversibility constraints were directly imposed in previous MILP path finding algorithms [14, 17]. Using FBA or pFBA as an initial step allows for low-flux paths to be found, and also reduces the paths to only those that are used in FBA or pFBA solutions. Additionally, many existing approaches prevent metabolic cycles from being found, but these cycles can be important in deciphering genome-scale modeling results. For example, the pathway involved in CO2 fixation requires using the oxaloacetate node and PPC reaction twice. Approaches that can enumerate metabolite cycles are thus useful for interpreting metabolic network behaviors.
Previous research efforts have focused mostly on finding the shortest paths between metabolites. However, the shortest path might not be used in a FBA or pFBA flux prediction. Even if all feasible paths were enumerated, it would be difficult to determine which ones were used in a particular flux distribution. Instead, by using FBA, pFBA, or FVA as an initial step, the metabolic modeling results can be used to ensure PathTracer paths (1) satisfy all COBRA constraints (not just mass balances), (2) are active in predicted flux distributions, and/or (3) are the most active paths. For example, the shortest feasible path from glucose to ethanol would use the Entner-Doudoroff pathway to make pyruvate (Figure 4C) and then convert pyruvate into ethanol. However, this is not the highest flux path in a mutant designed for ethanol production, where glycolysis is predicted to carry more flux than the Entner-Doudoroff pathway (Table 1). Weighting reaction steps used in paths by the inverse of their flux values helps to identify the highest flux paths between two metabolites. Together, the approaches developed here provide scalable and model-specific tools to help analyze metabolic networks and interpret genome-scale modeling results. These tools allow users to identify from the hundreds of active metabolic fluxes, what carbon-based metabolic routes are predicted by FBA (or other COBRA methods) to carry out chemical transformations of interest. Such tools would be useful for debugging models (e.g., answering how growth is predicted to occur under conditions where it should not be), identifying common metabolic precursors to commercial chemicals (Zhang, Tervo, and Reed, under review), and better characterizing metabolic behaviors and/or predictions (e.g., what canonical or non-canonical pathways are being used).
Supplementary Material
ACKNOWLEDGEMENT
This work was funded by NSF (NSF 1053712) and by an NHGRI training grant to the Genomic Sciences Training Program (T32HG002760 to CT). We also thank Caroline Mitchell for help editing the paper.
Abbreviations
- CTM
carbon transfer map
- COBRA
constraint-based reconstruction and analysis
- FBA
flux balance analysis
- MILP
mixed integer linear program
- pFBA
parsimonius flux balance analysis
- FVA
flux variability analysis
- glc-D
glucose
- pyr
pyruvate
- pep
phosphoenolpyruvate
- g6p
glucose-6-phosphate
- CoA
coenzyme A
- SSALx
NAD-dependent succinate-semialdehyde dehydrogenase
- SSALy
NADP-dependent succinate-semialdehyde dehydrogenase
- SPMS
spermidine synthase
- PPC
phosphoenolpyruvate carboxylase
- GGPTRCS
gamma glutamyl putrescine synthase
- OAA
oxaloacetate
Footnotes
AUTHOR CONTRIBUTIONS
CJT developed the algorithms, and processing scripts. CJT and JLR conceived of and designed the algorithms, performed all the simulations, composed all figures, analyzed results and wrote the paper. All authors read and approved the final manuscript.
CONFLICT OF INTEREST
The authors declare no financial or commercial conflict of interest.
REFERENCES
- [1].Orth JD, Thiele I, Palsson BO. What is flux balance analysis? Nat. Biotech. 2010;28:245–248. doi: 10.1038/nbt.1614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Zomorrodi AR, Suthers PF, Ranganathan S, Maranas CD. Mathematical optimization applications in metabolic networks. Metab. Eng. 2012;14:672–686. doi: 10.1016/j.ymben.2012.09.005. [DOI] [PubMed] [Google Scholar]
- [3].Lewis NE, Nagarajan H, Palsson BO. Constraining the metabolic genotype–phenotype relationship using a phylogeny of in silico methods. Nat. Rev. Micro. 2012;10:291–305. doi: 10.1038/nrmicro2737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Blum T, Kohlbacher O. MetaRoute: fast search for relevant metabolic routes for interactive network navigation and visualization. Bioinformatics. 2008;24:2108–2109. doi: 10.1093/bioinformatics/btn360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [5].Goesmann A, Haubrock M, Meyer F, Kalinowski J, Giegerich R. PathFinder: reconstruction and dynamic visualization of metabolic pathways. Bioinformatics. 2002;18:124–129. doi: 10.1093/bioinformatics/18.1.124. [DOI] [PubMed] [Google Scholar]
- [6].Karp PD, Paley SM, Krummenacker M, Latendresse M, et al. Pathway Tools version 13.0: integrated software for pathway/genome informatics and systems biology. Brief. Bioinform. 2010;11:40–79. doi: 10.1093/bib/bbp043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Faust K, Croes D, van Helden J. Metabolic Pathfinding Using RPAIR Annotation. J. Mol. Biol. 2009;388:390–414. doi: 10.1016/j.jmb.2009.03.006. [DOI] [PubMed] [Google Scholar]
- [8].Croes D, Couche F, Wodak SJ, van Helden J. Inferring meaningful pathways in weighted metabolic networks. J. Mol. Biol. 2006;356:222–236. doi: 10.1016/j.jmb.2005.09.079. [DOI] [PubMed] [Google Scholar]
- [9].Arita M. The metabolic world of Escherichia coli is not small. Proc. Natl. Acad. Sci. U S A. 2004;101:1543–1547. doi: 10.1073/pnas.0306458101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Wagner A, Fell DA. The small world inside large metabolic networks. Proc. Biol. Sci. 2001;268:1803–1810. doi: 10.1098/rspb.2001.1711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Brohee S, Faust K, Lima-Mendez G, Sand O, et al. NeAT: a toolbox for the analysis of biological networks, clusters, classes and pathways. Nucleic Acids Res. 2008;36:W444–451. doi: 10.1093/nar/gkn336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Ranganathan S, Maranas CD. Microbial 1-butanol production: Identification of non-native production routes and in silico engineering interventions. Biotechnol. J. 2010;5:716–725. doi: 10.1002/biot.201000171. [DOI] [PubMed] [Google Scholar]
- [13].Bonnet E, Calzone L, Rovera D, Stoll G, et al. BiNoM 2.0, a Cytoscape plugin for accessing and analyzing pathways using standard systems biology formats. BMC Syst. Biol. 2013;7:18. doi: 10.1186/1752-0509-7-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Pey J, Prada J, Beasley JE, Planes FJ. Path finding methods accounting for stoichiometry in metabolic networks. Genome Biol. 2011;12:R49. doi: 10.1186/gb-2011-12-5-r49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Simeonidis E, Rison SC, Thornton JM, Bogle ID, Papageorgiou LG. Analysis of metabolic networks using a pathway distance metric through linear programming. Metab. Eng. 2003;5:211–219. doi: 10.1016/s1096-7176(03)00043-0. [DOI] [PubMed] [Google Scholar]
- [16].Tervo CJ, Reed JL. FOCAL: an experimental design tool for systematizing metabolic discoveries and model development. Genome Biol. 2012;13:R116. doi: 10.1186/gb-2012-13-12-r116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Pey J, Planes FJ, Beasley JE. Refining carbon flux paths using atomic trace data. Bioinformatics. 2014;30:975–980. doi: 10.1093/bioinformatics/btt653. [DOI] [PubMed] [Google Scholar]
- [18].Ford LR, Fulkerson DR, editors. Flows in Networks. Princeton University Press; 2011. [Google Scholar]
- [19].Orth JD, Conrad TM, Na J, Lerman JA, et al. A comprehensive genome-scale reconstruction of Escherichia coli metabolism -- 2011. Mol. Syst. Biol. 2011;7 doi: 10.1038/msb.2011.65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Mahadevan R, Schilling CH. The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab. Eng. 2003;5:264–276. doi: 10.1016/j.ymben.2003.09.002. [DOI] [PubMed] [Google Scholar]
- [21].Lewis NE, Hixson KK, Conrad TM, Lerman JA, et al. Omic data from evolved E. coli are consistent with computed optimal growth from genome-scale models. Mol. Syst. Biol. 2010;6:390. doi: 10.1038/msb.2010.47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Burgard AP, Nikolaev EV, Schilling CH, Maranas CD. Flux Coupling Analysis of Genome-Scale Metabolic Network Reconstructions. Genome Res. 2004;14:301–312. doi: 10.1101/gr.1926504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Kumar VS, Maranas CD. GrowMatch: An Automated Method for Reconciling In Silico In Vivo Growth Predictions. PLoS Comput. Biol. 2009;5:e1000308. doi: 10.1371/journal.pcbi.1000308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Reed JL, Patel TR, Chen KH, Joyce AR, et al. Systems approach to refining genome annotation. Proc. Natl. Acad. Sci. U S A. 2006;103:17480–17484. doi: 10.1073/pnas.0603364103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Barua D, Kim J, Reed JL. An Automated Phenotype-Driven Approach (GeneForce) for Refining Metabolic and Regulatory Models. PLoS Comput. Biol. 2010;6:e1000970. doi: 10.1371/journal.pcbi.1000970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Machado D, Herrgard M. Systematic evaluation of methods for integration of transcriptomic data into constraint-based models of metabolism. PLoS Comput. Biol. 2014;10:e1003580. doi: 10.1371/journal.pcbi.1003580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Pharkya P, Burgard AP, Maranas CD. OptStrain: A computational framework for redesign of microbial production systems. Genome Res. 2004;14:2367–2376. doi: 10.1101/gr.2872004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Jeong H, Tombor B, Albert R, Oltvai ZN, Barabasi AL. The large-scale organization of metabolic networks. Nature. 2000;407:651–654. doi: 10.1038/35036627. [DOI] [PubMed] [Google Scholar]
- [29].Reed JL, Vo TD, Schilling CH, Palsson BO. An expanded genome-scale model of Escherichia coli K-12 (iJR904 GSM/GPR) Genome Biol. 2003;4:R54. doi: 10.1186/gb-2003-4-9-r54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Fuchs G. Alternative pathways of carbon dioxide fixation: insights into the early evolution of life? Annu. Rev. Microbiol. 2011;65:631–658. doi: 10.1146/annurev-micro-090110-102801. [DOI] [PubMed] [Google Scholar]
- [31].Hamilton JJ, Dwivedi V, Reed JL. Quantitative Assessment of Thermodynamic Constraints on the Solution Space of Genome-Scale Metabolic Models. Biophys. J. 2013;105:512–522. doi: 10.1016/j.bpj.2013.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].McFall E, Newman EB. Amino Acids as Carbon Sources. In: Neidhardt FC, editor. Escherichia coli and Salmonella: Cellular and Molecular Biology. ASM Press; Washington DC: 1996. pp. 358–379. [Google Scholar]
- [33].Patte JC. Biosynthesis of Threonine and Lysine. In: Neidhardt FC, editor. Escherichia coli and Salmonella: Cellular and Molecular Biology. ASM Press; Washington DC: 1996. pp. 528–541. [Google Scholar]
- [34].Lee SK, Newman JD, Keasling JD. Catabolite repression of the propionate catabolic genes in Escherichia coli and Salmonella enterica: evidence for involvement of the cyclic AMP receptor protein. J. Bacteriol. 2005;187:2793–2800. doi: 10.1128/JB.187.8.2793-2800.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Feldman HJ, Dumontier M, Ling S, Haider N, Hogue CW. CO: A chemical ontology for identification of functional groups and semantic comparison of small molecules. FEBS Lett. 2005;579:4685–4691. doi: 10.1016/j.febslet.2005.07.039. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.