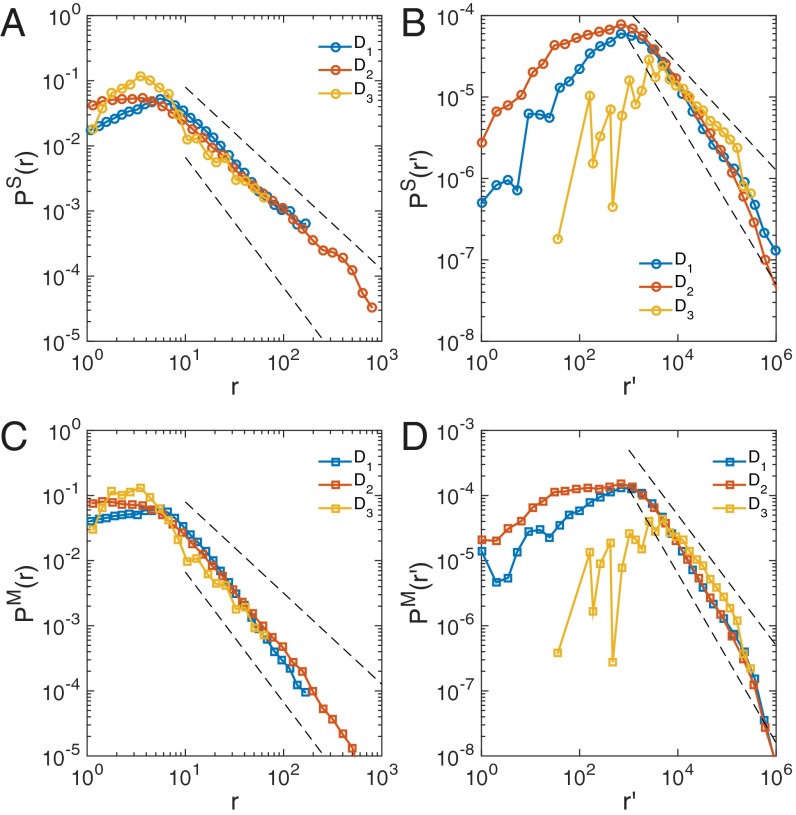
Fig. 1.

Communication and jump size distance distributions. (A) Communication distance distributions measured in geodesic distance r, $P^S\left(r\right)$, for all three datasets. Here, r measures the distance between two users when they communicate with each other via either phone calls or SMS. r is measured in the unit of kilometers. (B) Rank distributions $P^S(r\prime )$ for the three datasets follow a power law tail with exponents ${\beta }^{r\prime }=0.89$ for $D1$, ${\beta }^{r\prime }=1.00$ for $D2$, and ${\beta }^{r\prime }=0.64$ for $D3$. (C) Jump size distribution $P^M\left(r\right)$ measured in geodesic distance r follows a power law distribution. (D) Rank jump size distribution $P^M(r\prime )$ for rank $r\prime$ follows a power law distribution with exponent ${\alpha }^{r\prime }$ between 1.2 and 1.3 for $D1$ and $D2$ and ${\alpha }^{r\prime }\approx 1$ for $D3$. Here we mainly focus on large r (or $r\prime$) regime, fitting the tail part of the distributions. For fat-tailed distributions such as power law distributions, the tail part is the most important, determining the convergence/divergence of moments of distributions. The small r (or $r\prime$) regime before the peak is often referred to as small value saturations. Dashed lines serve as guide to the eye.