Real-time transposable element activity in individual live cells

Significance

We have followed in real time how transposable elements, or “jumping genes,” move around in the genome of a living organism. Using a simple plasmid-borne transposable element, we have measured directly and precisely how frequently cells are affected by transposable elements and what factors contribute to their activity. We find the activity of this simple transposable element to be surprisingly rich, depending upon the host cell’s growth and environmental factors. Application of this system to more complex natural transposable elements will enable a quantitative understanding of these fundamental dynamical elements of all genomes, informing our understanding of genome plasticity and the mutations that can give rise to disease and drive evolution.

Abstract

The excision and reintegration of transposable elements (TEs) restructure their host genomes, generating cellular diversity involved in evolution, development, and the etiology of human diseases. Our current knowledge of TE behavior primarily results from bulk techniques that generate time and cell ensemble averages, but cannot capture cell-to-cell variation or local environmental and temporal variability. We have developed an experimental system based on the bacterial TE IS608 that uses fluorescent reporters to directly observe single TE excision events in individual cells in real time. We find that TE activity depends upon the TE’s orientation in the genome and the amount of transposase protein in the cell. We also find that TE activity is highly variable throughout the lifetime of the cell. Upon entering stationary phase, TE activity increases in cells hereditarily predisposed to TE activity. These direct observations demonstrate that real-time live-cell imaging of evolution at the molecular and individual event level is a powerful tool for the exploration of genome plasticity in stressed cells.

A transposable element (TE) is a mobile genetic element that propagates within its host genome by self-catalyzed copying or excision followed by genomic reintegration (1). TEs exist in all domains of life, and the activity of TEs necessarily generates mutations in the host genome. Consequently, TEs are major contributors to disease (2–8), development (9, 10), and evolution (11, 12); they are also used as molecular tools in synthetic biology and bioengineering (13).

Despite their ubiquity and importance, surprisingly little is known about the behavior and dynamics of TE activity in living cells. TE propagation rates can be inferred from comparative phylogenetic analyses of related organisms (14–20) or endpoint analyses of TE abundance within populations (11, 21–23). By making assumptions about the mechanisms of TE proliferation, models can be constructed to describe the distribution of TEs within genomes over evolutionary time scales, and sequenced genomes can be analyzed and fit to TE proliferation models to infer phylogeny of TE copies and estimate their rates of propagation (24). However, most sequencing techniques require bulk sampling of cells to provide genetic material, and sequencing is therefore generally an average over many cells. As a result, without extremely deep or single-cell sequencing techniques, most current methods are sufficient to detect only those TE events that have occurred in the germ line and therefore appear in every somatic cell in the body (25).

TE rates can also be estimated by measuring relative abundances in populations that have been allowed to mutate over laboratory time scales. One of the first examples of this approach was that by Paquin and Williamson (23) to study the effects of temperature on the rate of integration of Ty retrotransposons in Saccharomyces cerevisiae after growth for 6–8 generations, resulting in yeast resistant to the antibiotic antimycin A; they estimated a rate of transposition of 10⁻⁷–10⁻¹⁰ insertions into a particular region of the yeast genome per cell per generation. As another example, sequencing of Escherichia coli at intervals in Lenski’s long-term evolution experiments also provided a means to estimate transposition frequency, which they estimate to be on the order of 10⁻⁶ per cell per hour (11). However, such measurements yield information on only the relative abundance of extant TE-affected cells in the population, and dynamic rates must again be inferred through models of population growth that may or may not be accurate.

The limitations described above mean that there is a dearth of information regarding TE behavior in individual living cells in vivo and the effects of TE activity on those cells. Additionally, estimation of transposition frequency from either phylogenetic comparisons or population endpoint analyses both suffer from the same serious and fundamental limitation: they are only able to detect those events that have not gone to extinction in the population, and therefore these methods almost certainly underestimate the actual rates of transposition. An analogous situation previously existed in the case of the dynamics of horizontal gene transfer: phylogenetically inferred rates of horizontal gene transfer are typically 1 per 100,000 y, whereas direct visual observation in experiments (26) has shown that the actual transfer rate is many orders of magnitude faster, about one per generation time.

To quantitatively study the dynamics of TE activity and its controlling factors in real time and in individual cells, we have constructed a TE system based on the bacterial TE IS608 in E. coli. IS608 is a representative of the IS200/IS605 family of transposable elements, which all transpose through similar mechanisms. The IS200/IS605 family is widely distributed, with 153 distinct members spread over 45 genera and 61 species of eubacteria and archaea (27). Transposition occurs by exact excision from a single DNA strand (21, 28–32). Imperfect palindromic sequences flanking the ends of the TE form unique structures that are recognized by transposase protein TnpA, which can act as a homodimer to excise the TE. The excised TE–TnpA complex can locate and integrate the TE adjacent to a short, specific sequence (TTAC). Our construct exploits the structure and regulation of the TE to allow the direct detection and quantification of TE activity in live cells using a suite of novel fluorescent reporters.

Results

TE Observation System.

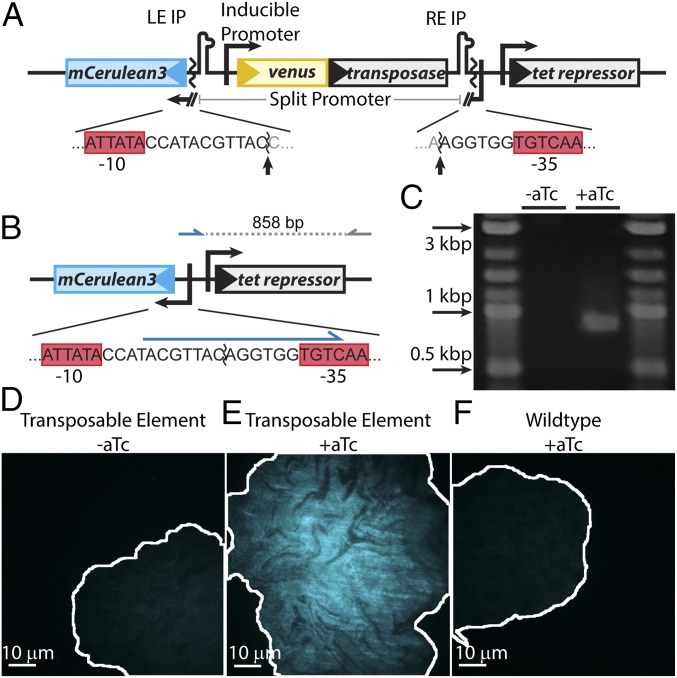
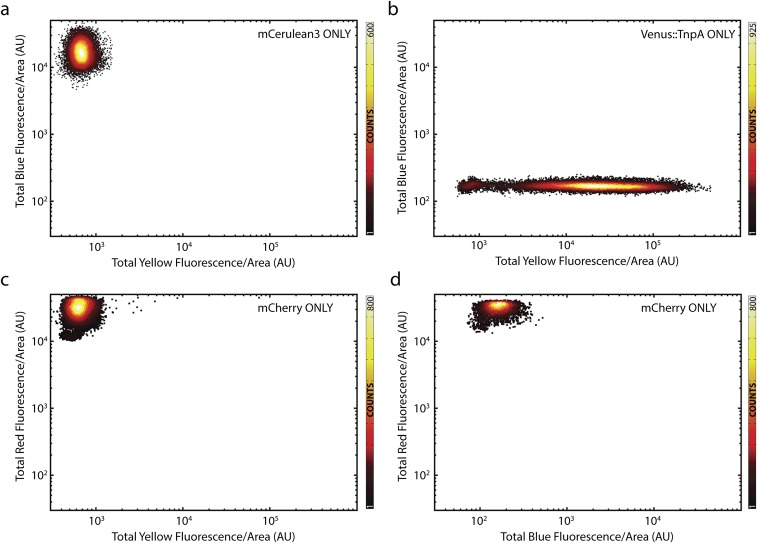
A diagram illustrating the TE system is shown in Fig. 1A. The TE is composed of the transposase coding sequence, tnpA, flanked by a left end imperfect palindromic sequence (LE IP) and right end imperfect palindromic sequence (RE IP), which are the recognition and cleavage sites for TnpA. tnpA is expressed using the promoter P_LTetO1, which is repressed by tet repressor. P_LTetO1 is derived from the E. coli transposable element Tn10 and titratable over a ∼100× range with anhydrotetracycline (aTc) (33). The use of this inducible promoter allows for simple and precise control of TnpA levels within individual cells. The TE splits the −10 and −35 sequences of a strong constitutive P_lacIQ1 promoter (34) for the expression of the blue reporter mCerulean3 (35). As shown in Fig. 1B, when transposase production is induced, the TE can be excised, leading to reconstitution of the promoter. The resulting cell expresses mCerulean and fluoresces blue, indicating that an excision event has occurred. The N terminus of TnpA is translationally fused to the bright yellow reporter Venus (36), and the cells constitutively express the red reporter mCherry (37) to aid in image segmentation. Measurements of blue, yellow, and red fluorescence of controls demonstrate no cross-talk in our optical setup (Fig. S1). The TE is hosted in the low copy number plasmid pJK14 with a pSC101 replication origin (38).

Fig. 1.

Design and validation of the TE system. (A) The promoter for mCerulean3 is interrupted by the transposable element, the ends of which are demarcated by left end and right end imperfect palindromic sequences (LE IP and RE IP). The transposase, tnpA (gray), is expressed from the promoter P_LtetO1, which is inducible with aTc. The sequences of the promoter/TE junction and −10 and −35 sequences (red boxes) are shown below the diagram, and the sites cleaved by transposase are indicated by arrows. (B) Upon excision, the promoter for mCerulean3 is reconstituted and the cell fluoresces blue. The sequence of the reconstituted promoter is shown below the diagram. A primer designed to bind to the unique sequence formed after promoter reconstitution (blue arrow) was used to verify excision by PCR, generating an 858-bp amplicon. (C) PCR amplification using these primers only generates the 858-bp product upon induction, thus verifying excision. (D–F) Colony morphology after growth on agarose pads. Uninduced TE-carrying cells (D) and wild-type cells exposed to 20 ng/mL aTc (F) show homogeneous, low blue autofluorescence. Conversely, TE-carrying cells induced with 20 ng/mL aTc (E) show bright, inhomogeneous blue fluorescence. The brightness scale for all three images is identical. The borders of the colonies are outlined in white.

Fig. S1.

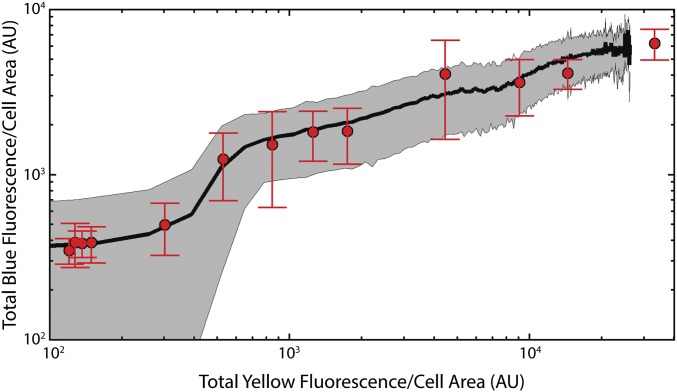
No cross-talk between fluorescent channels. (A and B) Scatterplots of blue vs. yellow fluorescence for controls expressing only (A) mCerulean3 (n = 17,137 cells) and (B) titration of Venus-TnpA (n = 65,791 cells) with [aTc] ∈ [0, 100] ng/mL. (C and D) Scatterplots of (C) red vs. yellow (n = 31,376 cells) and (D) red vs. blue fluorescence (n = 21,125 cells) of a strain expressing only mCherry.

Verification of TE Observation System.

We first confirmed that the TE excises upon induction of transposase production. PCR was performed using primers that bind to the unique sequence formed upon excision, and cells containing the TE and induced with aTc yielded product with amplicons of the expected length (Fig. 1C). We next verified that transposase induction results in expected patterns of fluorescence corresponding to TE excision. When TE-carrying E. coli are grown on agarose pads with aTc, the resulting microcolonies exhibit spatially distinct bright and dark regions of blue fluorescence (Fig. 1E). This observation is expected from plasmids expressing blue fluorescent proteins after some have undergone TE excision, followed by plasmid inheritance by daughter cells, and will be discussed in more detail below. Conversely, microcolonies arising from an identically treated wild-type negative control strain carrying no plasmids and an uninduced TE-carrying strain are fluorescently dim and homogeneous (Fig. 1 D and F).

Quantification of Excision Response to Transposase Concentration.

It is reasonable to expect that TE excision probabilities may be a function of intracellular transposase concentration. This straightforward expectation has proven difficult to experimentally characterize, however, due to low-throughput sampling of transposase concentration provided by population sequencing and other bulk techniques (39). By comparing the intensity of yellow fluorescence and blue fluorescence of single cells titrated over a wide range of transposase inducer, we were able to determine the in vivo excision response function to transposase concentration.

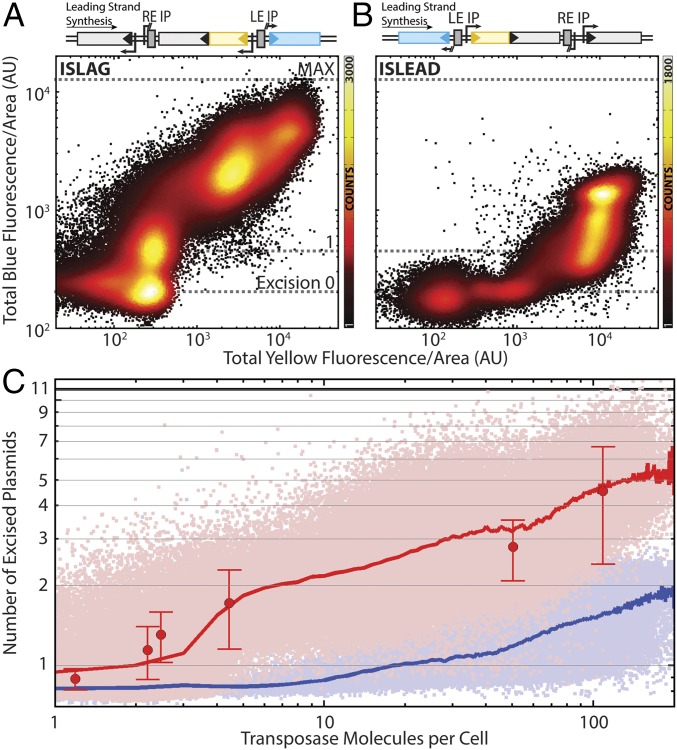
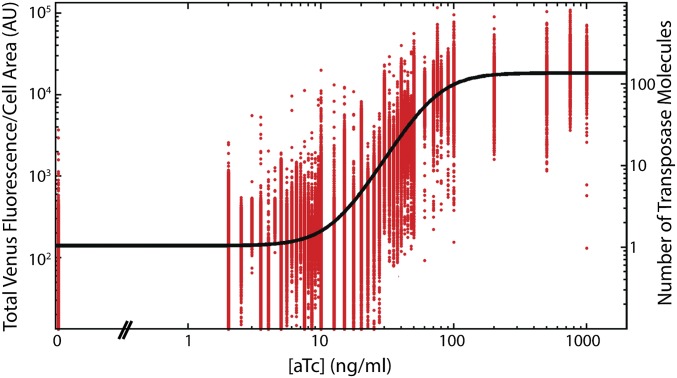
TE-carrying cells were grown in medium titrated with aTc concentrations ranging from 0 to 1,000 ng/mL. We constructed two versions of the TE, one with the imperfect palindromic sequences encoded in the leading strand (ISLEAD) and the other with the imperfect palindromic sequences encoded in the lagging strand (ISLAG). After ∼12–13 doublings, each sample was imaged using highly inclined and laminated optical sheet (HILO) laser illumination (40, 41). Fig. 2 shows scatterplots of blue fluorescence vs. yellow fluorescence for individual cells carrying ISLAG (Fig. 2A) or ISLEAD (Fig. 2B). The response functions for ISLAG and ISLEAD are qualitatively different, with the ISLAG construct responding more quickly at low aTc concentrations and the ISLEAD construct responding at higher aTc concentrations. The transposase promoter’s nonlinear response to aTc (Fig. S2) results in nonuniform count densities along the x axis. To determine if translational fusion of Venus to TnpA affected transposase expression, a version of ISLAG without Venus fused to TnpA was also assayed. The construct showed quantitatively identical behavior (Fig. S3).

Fig. 2.

TE excision response function. Scatterplots of blue vs. yellow total cellular fluorescence divided by cell area for TE encoded in the (A) lagging (N_cells = 192,965) and (B) leading (N_cells = 101,709) strand of the host plasmid. Colors indicate number of counts in each bin of a 500 × 500 grid covering the data. (C) The same data as in A and B with absolute axes. The y axis is expressed in terms of the absolute number of excised plasmids, and the x axis is scaled to absolute number of transposase molecules per cell. Light-red and -blue points are lagging and leading strand data from A and B, respectively. Red and blue lines are excised plasmid number averaged according to transposase molecules binned as integer quantities. Large red points indicate the number of excised plasmids as measured by qPCR; error bars are the SEM of three experimental replicates. See also Fig. S3.

Fig. S2.

Titration of transposase with aTc. Venus-TnpA expression as a function of inducer concentration for pJK14-ISLAG (red points). These points are fit to a Hill function (black line) to extract quantitative features of the response $f\left(\left[\text{aTc}\right]\right)=A\cdot \left[1+\omega {\left(\frac{\left[\text{aTc}\right]}{K}\right)}^n/\{1+{\left(\frac{\left[\text{aTc}\right]}{K}\right)}^n\right\}],$ where ω is the capacity or fold change of the response, K is an effective dissociation constant, n is the Hill coefficient measuring the sensitivity of the response, and A is an overall scaling factor (58). We find ω = 127, K = 71.5 nM, and n = 2.8. The scaling between Venus fluorescence (left y axis) and number of TnpA molecules per cell (right y axis) is determined by analysis of fluctuations in Venus-TnpA bleaching kinetics as binomial noise (Estimation of Absolute Venus-TnpA Concentration and Fig. S4).

Fig. S3.

Venus fusion to TnpA has no effect on transposase activity. Mean blue vs. yellow fluorescence behavior of pJK14-ISLAG (black line) compared with that of pJK14-ISLAGMin (red points; N_cells = 69,868), a version of the TE with no Venus tag on the transposase. Because the pJK14-ISLAGMin strain shows no yellow fluorescence, the data are plotted such that the abscissa of each red point corresponds to the value of the best-fit Hill function from Fig. S2 at the corresponding aTc concentrations. SD of the ISLAG response is shown as the gray shaded region, and SD of ISLAGMin points are red error bars; SEM is smaller than the size of the symbols.

We next quantified the number of transposase molecules and induced excisions based on the intensity of yellow and blue fluorescence. The result is shown in Fig. 2C, with mean response functions of ISLAG and ISLEAD shown as red and blue lines, respectively.

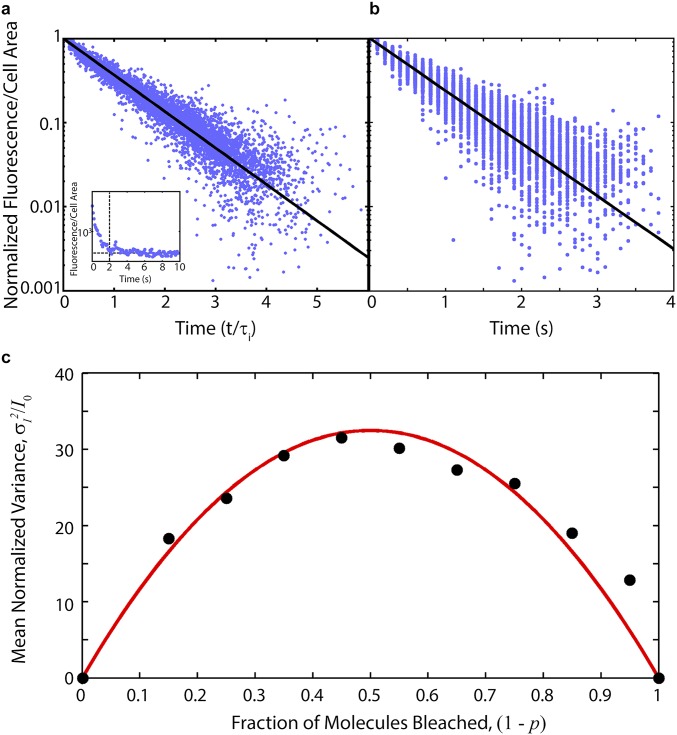
To estimate the absolute number of transposase molecules induced, the bleaching kinetics of Venus-TnpA were analyzed based on a theoretical technique developed by Nayak and Rutenberg (42), discussed in detail in SI Experimental Procedures. ISLAG cells were grown as described above, and transposase expression was induced with 100 ng/mL aTc. At OD₆₀₀ = 1.0, cells were mounted on a slide and their bleaching kinetics recorded via fluorescence microscopy. By recognizing fluctuations from the mean bleaching kinetics of Venus-TnpA as binomial noise, the bleaching curves of individual cells can be analyzed to estimate the constant of proportionality, ν, relating fluorescent intensity to the number of fluorescent molecules. We find ν = 130 ± 10 from the analysis of 419 cells (Fig. S4 and SI Experimental Procedures).

Fig. S4.

Estimation of absolute transposase numbers from Venus-TnpA bleaching kinetics. (A) Individual bleaching curves are exponential. Bleaching curves of normalized Venus-TnpA fluorescence vs. time in units of each curve’s fitted decay constant from 419 individual cells (blue points) compared with exponential bleaching kinetics (black line). (Inset) A representative single cell bleaching trace over 10 s. We truncate the bleaching curve (e.g., at vertical dashed line) when the fluorescence comes within 100 AU of the background (horizontal dashed line). (B) Individual bleaching traces (blue points) with 100 ms exposure time compared with the mean bleaching kinetics (black line). The mean decay constant is τ = 0.68 ± 0.01 s. Fluctuations from the mean bleaching kinetics are binomial noise, and analysis of the variance allows estimation of absolute Venus-TnpA numbers. (C) Mean normalized variance from 419 cells (black points) vs. fraction of bleached molecules, (1 – p). The proportionality constant, ν, relating fluorescence to number of molecules is related to the area under the best fit parabola [red line], yielding ν = 130 ± 10.

To determine how blue fluorescence intensity represents excision numbers, we measured the mean blue fluorescence of a wild-type negative control carrying no plasmids, as well as a control in which every plasmid expresses mCerulean. Their average intensities correspond to the mean fluorescence of cells with no excisions and cells with all TEs excised, respectively (Fig. 2 A and B, excision 0 and MAX). From the excision response curve, one can see a clear distinction in the blue fluorescence of cells with no excisions and those with one TE excision (Fig. 2 A and B, line 1). And our simulation shows that blue fluorescence intensity is expected to be proportional to the number of excised plasmids (Fig. S5). Therefore, by using quantitative PCR (qPCR) to determine the average plasmid copy number in each cell, the y axis can be scaled in terms of the average absolute number of excised plasmids.

Fig. S5.

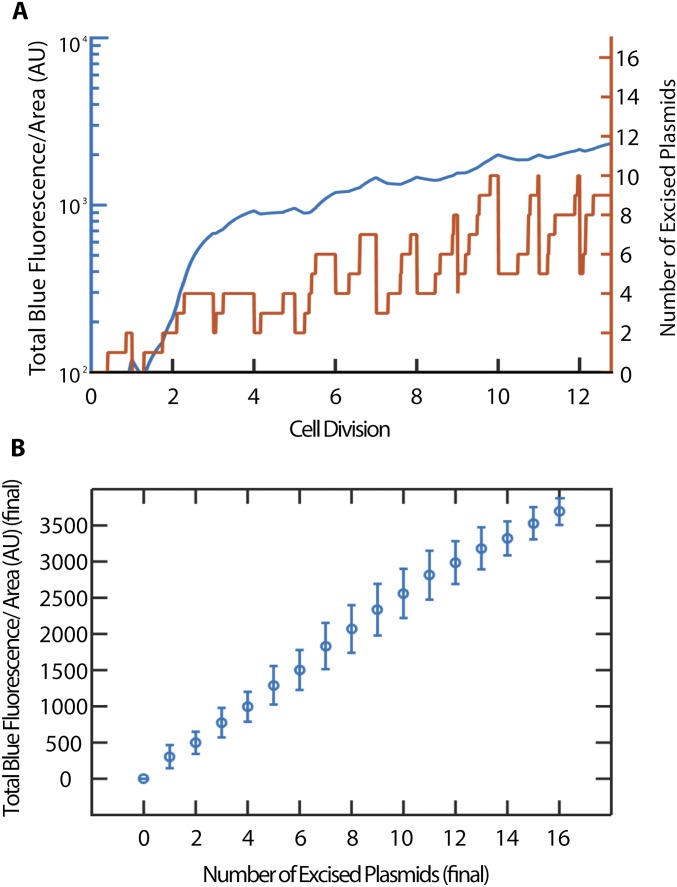
Simulated blue fluorescence as a function of plasmid excision and cell growth. (A) Time trace of TE-excised plasmid number inside a single simulated cell (orange) and time trace of blue fluorescence level of the same simulated cell (blue). Upon cell division, fluorescent proteins and plasmid numbers are halved. (B) Total blue fluorescence per area (AU) vs. number of excised plasmids at time of imaging, as a result of 10,000 iterations of the simulation. The plot shows that the blue fluorescence per area is expected to be proportional to the number of excised plasmids. Error bars are SDs of the simulated values resulting in respective excised plasmid number.

To further verify that fluorescence accurately represents TE excision number, qPCR measurements of lagging strand TE excisions over a range of transposase inducer concentrations were performed (Fig. 2C, red points) using primers that produce an amplicon only when excised plasmid is present. At the highest transposase numbers we achieve, ∼50% of the average total 11–12 plasmids per cell are excised (Fig. S6).

Fig. S6.

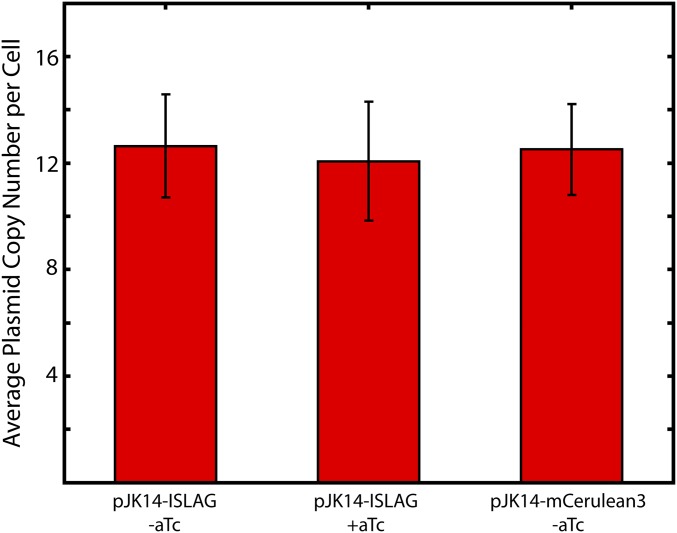
TE activity does not affect absolute average plasmid copy number. Average plasmid copy number per cell determined by quantitative PCR for uninduced and induced pJK14-ISLAG plasmid (first and second columns) and the mCerulean3 only control plasmid (third column). Error bars are SEM of three experimental replicates for each sample. Over all three samples, the average copy number per cell is 12.4 ± 3.3, in agreement with Lutz and Bujard’s measurement of pSC101 copy number of 10–12 plasmids per cell (33).

Observing Real-Time Kinetics.

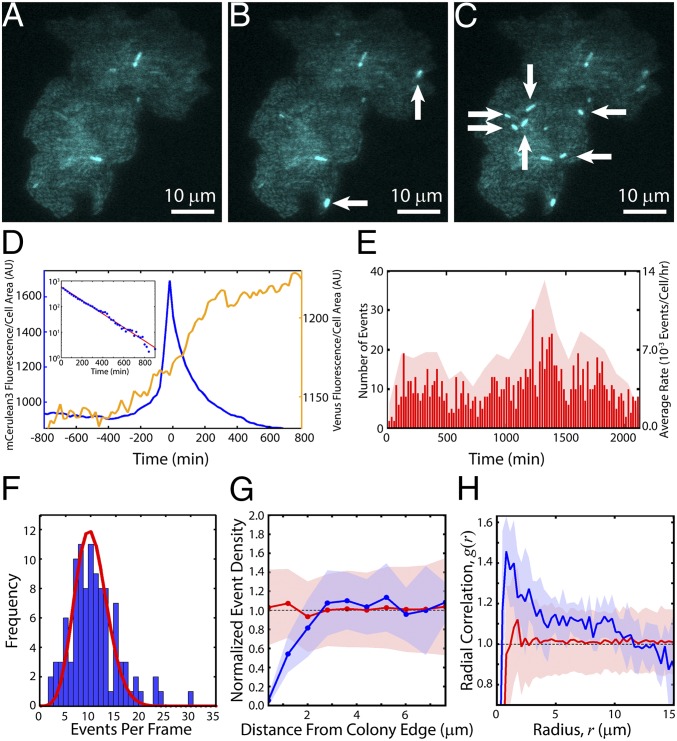
By growing TE-carrying cells on agarose pads including aTc under the microscope, TE excision events can be detected in real time and their rates and statistics determined through direct observation. We find that TE activity changes as cells undergo different phases of growth, and that TE activity correlates to where cells are located within a colony.

Excision Rates Depend on Growth State of Cells.

At high-inducer concentrations (>10 ng/mL aTc; Fig. 1E), a large fraction of cells immediately experiences TE events and fluoresces blue. At low-inducer and transposase concentrations (<10 ng/mL aTc), we can observe individual excision events as bright flashes of blue fluorescence whose rate depends upon the growth state of the cells. As cells initially adapt to the pad, some fraction rapidly fluoresce blue, indicating TE excision. Once cells enter exponential growth, the frequency of cells becoming fluorescent drops to nearly zero; the fluorescence patterns observed in mature microcolonies at low inducer concentrations (Fig. 3A) arise primarily from inheritance of the initial excision events. However, upon entering final growth arrest, some cells begin to emit bright blue fluorescence (Fig. 3 A–C and Movie S1) accompanied by an increase in yellow fluorescence (Fig. 3D and Movie S2). The polar localization of Venus-TnpA seen in Movie S2 is a known consequence of nucleoid condensation and volume exclusion in stationary phase (41, 43). Note in Fig. 3D that the excision event (blue line) is preceded by a weak increase in transposase levels (yellow fluorescence), indicating transposase-induced excision. Control strains, including a wild-type TE-less strain exposed to aTc, TE-carrying cells not exposed to aTc, and cells constitutively expressing mCerulean3, do not show similar bursts of fluorescence (Movie S3).

Fig. 3.

Real-time TE kinetics. Colony induced with 5 ng/mL aTc undergoing excision events at (A) t = 0 (time of first detected events, after ∼10 h of growth), (B) t = 40 min, and (C) t = 60 min. New events are indicated by white arrows. (D) mCerulean3 and Venus-TnpA traces for an average event. TE events were aligned with peak mCerulean3 intensity at t = 0. Shown is the mean mCerulean3 (blue, left y axis) and Venus-TnpA (yellow, right y axis) fluorescence per cell area as a function of time averaged over 773 events. (Inset) Decay of mCerulean3 fluorescence as a function of time. Red line is a fit to an exponential $f\left(t\right)=A\exp (-bt)$, with A = 589 and b = −0.006 min⁻¹, consistent with photobleaching. (E) Raster plot of all events in a single experiment (red lines, left y axis) with t = 0; N_colonies = 12, N_cells = 4,858, N_events = 1,114. The average rate was 6.3 ± 2.6 × 10⁻³ events per cell per hour. Red shaded region shows the average rates during 100-min intervals (right y axis). (F) Blue bars: frequency of the number of events per frame. Red line: distribution of events per frame expected from a Poisson process with an average rate of 6.3 × 10⁻³ events per cell per hour. (G) Within each colony, we determine the event densities within annuli of width 0.8 μm at various distances from the colony edge (Fig. S7). We then took an ensemble average over all colonies, where the density in each colony is normalized by the mean event density over the entire colony. Blue line: mean normalized density of events in 0.8-μm-wide annuli vs. the distance of the center of each annulus from the colony edge; shaded blue region is the SD. Red line: mean normalized density obtained from simulations of randomly spaced events; shaded red region is the SD. (H) Blue line: mean pair correlation function, g(r), of events; shaded blue region is the SD. Red line: g(r) of randomly spaced events obtained from simulations; shaded red region is the SD.

Excision Event Rate Is Constant Once Initiated.

Automated identification of TE fluorescence events within each colony (Movie S4) reveals that events begin occurring with the onset of growth arrest and continue at a rate that remains approximately constant for >35 h (Fig. 3E). The average event rate for this experiment, consisting of 12 colonies and ∼5,000 cells, was 6.3 ± 2.6 × 10⁻³ events per cell per hour. The temporal statistics are consistent with events, once initiated upon growth arrest, occurring randomly in time as described by Poisson statistics (Fig. 3F).

Excision Events Are Spatially Correlated.

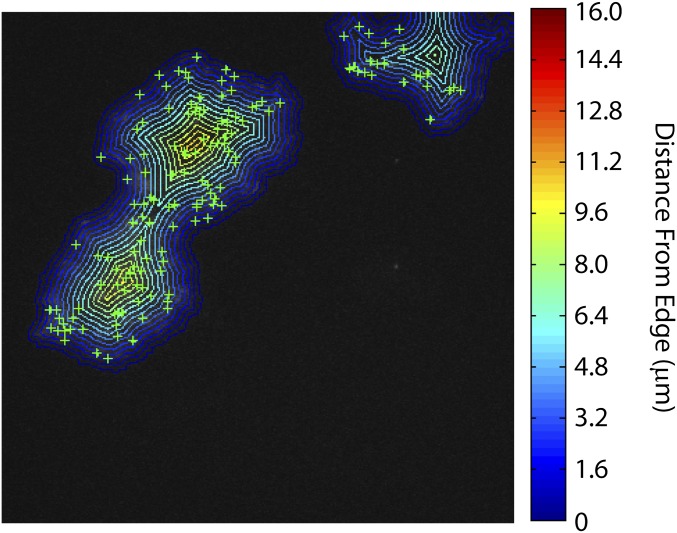
Events are not uniformly random in space and are instead spatially clustered and dependent upon the location in the colony. Events are less common within ∼3 μm (∼5 cell widths) of the colony edge compared with the center (Fig. 3G and Fig. S7). The mean pair radial correlation, g(r), also shows that events are clustered together (Fig. 3H, blue line, and SI Experimental Procedures).

Fig. S7.

Event density as a function of distance from colony edge. Within each colony, we determine the number of events (green plus signs) lying within annuli of width 0.8 μm at various distances from the colony edge. The density of events in colony i within an annulus at radius r, ρ_i(r), is calculated as the number of events within that annulus, N_i(r), divided by the area of the annulus, A_i(r), ρ_i(r) = N_i(r)/A_i(r). The data shown in Fig. 3G is the ensemble average over all colonies, where the density in each colony is normalized by the mean event density over the entire colony. In this image, the edges of each annulus are shown, and the color indicates the distance from the edge of the colony as given by the color bar at right.

We performed simulations of E. coli growth into microcolonies combined with random distributions of TE events to determine the expected properties of g(r) arising from randomly spaced TE events within an E. coli colony. Simulations were used to generate 200 different microcolony morphologies, each starting from a single cell and ending upon reaching a size representative of those we observe in our experiments (∼300 cells with a diameter of ∼15–16 μm). After growth arrest, 15% of the cells within each colony morphology were chosen at random to undergo TE events, a rate representative of the average final number of affected cells in each colony we observe experimentally. By comparing g(r) between experiment and simulation, we find that the density of events in adjacent cells in our experiment is ∼1.4× greater than expected compared with the simulation of events randomly distributed in space (Fig. 3H, red line, Movie S5, and SI Experimental Procedures).

Distribution of Rates Is Consistent with Additional Control by a Heritable Luria–Delbrück Process.

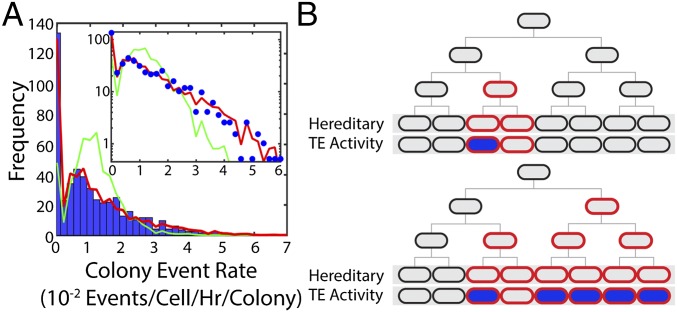
The nonuniform event distributions in space suggest that local environmental differences and/or a hereditary process are influencing TE activity. A distribution of event rates determined from 984 colonies is shown in Fig. 4A, with a mean rate of 11.8 ± 12 × 10⁻³ events per cell per hour per colony. (This is compatible with overall number of events per frame following a Poisson distribution; Fig. 3F and SI Experimental Procedures.) To explain the distribution of colony event rates shown in Fig. 4A, we simulated a two-step process (44, 45). First, in a Luria–Delbrück process after cells are placed on the pad, some stochastic heritable change can occur with constant probability during exponential growth that predisposes cells to TE activity (Fig. 4B). In the simulation, 10,000 cell colonies were simulated to grow until they reached colony sizes drawn from the colony size distribution observed in the experiment. While in growth, a heritable change occurs in a daughter cell after each division with probability p_h. From the affected cell, the change is inherited by all of its descendants. In growth arrest, any cell that has inherited the change can then experience a TE excision with probability p_e. A good fit of event densities was found (Fig. 4A, red line) by searching through the two parameters with a goodness criterion (SI Experimental Procedures). This analysis and the quality of the fit strongly suggest that the average event rate in each colony is determined by some stochastic, heritable change occurring in the lineage—for example, expression bursts, or lack thereof, of long-lived tet repressor protein.

Fig. 4.

Event rates are determined by a stochastic heritable change. (A) Blue bars: distribution of average event rates for individual colonies with [aTc] = 5 ng/mL; N_colonies = 984. The mean rate of this distribution is 11.8 ± 12 × 10⁻³ events per cell per hour per colony. Red line: result of a two-step process simulated using the experimental distribution of colony sizes. Green line: result of a Poisson process with the mean rate of the experimental distribution. (Inset) Same data with logarithmic y axis. (B) Cartoon picture illustrating the Luria–Delbrück process used in our simulation where some fraction of cells inherit a trait that predisposes them to TE activity (red outline), and of those cells some fraction fluoresce blue, indicating TE activity (blue fill).

SI Experimental Procedures

Strains and Media.

Experiments were performed using E. coli K-12 MG1655 Δlac (41, 43, 50, 51, 55) expressing the red fluorescent protein mCherry (37) from a strong P_lacIQ constitutive promoter integrated into the nth chromosomal locus located near the replication terminus (41, 50, 55). Molecular cloning and plasmid manipulations were performed using DH5α as a host strain.

Cells for measurement of the TE excision response function were grown in M63 minimal medium [100 mM KH₂PO₄, 15 mM (NH₄)₂SO₄, 1 mM MgSO₄, 1.7 μM FeSO₄, 0.5% (wt/vol) thiamine, pH adjusted to 7.0 with KOH] with 0.5% (vol/vol) glycerol as carbon source. Antibiotics were added to the medium as appropriate for plasmid maintenance, and different concentrations of aTc (Sigma Aldrich) were added to induce transposase production.

Cells for real-time measurement of TE activity were imaged on 2% (wt/vol) agarose pads made with M63 minimal medium with 0.5% (vol/vol) glycerol as carbon source + 25 μg/mL kanamycin and 5 ng/mL anhydrotetracycline.

Plasmid Construction.

The low copy number plasmid pJK14 (38) was used to host the TE in all experiments. pJK14 has a pSC101 replication origin and is replicated unidirectionally, i.e., there is a well-defined leading and lagging strand. Plasmid copy number is tightly controlled through the positive feedback of the plasmid-encoded protein RepA (52). Additionally, pJK14 is actively segregated to daughter cells through the pSC101 par system (53).

Plasmid pJK14-ISLEAD was designed using Vector NTI software (Life Technologies) and synthesized de novo by GENEWIZ Gene Synthesis Services (GENEWIZ, Inc.).

To generate pJK14-ISLAG, pJK14-ISLEAD was digested with I-SceI (New England Biosciences), purified (QIAquick PCR Purification Kit; QIAGEN), religated, and transformed into DH5α. Plasmids purified from eight resulting colonies were digested with PciI (NEB) and run through a gel to verify that the TE had been successfully reoriented.

Plasmid pJK14-ISLEAD and pJK14-ISLAG were used to create versions of the TE in which the Venus (36) fusion is removed from TnpA, pJK14-TnMinLEAD and pJK14-TnMinLAG. The P_LtetO1-venus-tnpA fragment was removed from pJK14-ISLAG through digestion with BamHI and NheI, gel purification, and dephosphorylation with Antarctic phosphatase (NEB). Untagged tnpA from pJK14-ISLEAD was amplified using Phusion Flash master mix (Life Technologies) and the primers BamHI-P_LtetO1-tnpA F 5′-CGTATTATCCGGATCCGTGATAGAGATTGACATCCCTATCAGTGATAGAGATACTGAGCACATCAGCAGGACGCACTGACCGAATTCATTAAAGAGGAGAAAATGAGTAACGCTGTTTTATACAAAA-3′ and tnpA-NheI R 5′-CACTTAAGACTCGAGTTATAGAGCTTTTGTTTGTAGGTTA-3′.

The PCR product was digested with BamHI and NheI and ligated into the pJK14-ISLAG backbone to generate pJK14-TnMinLEAD and pJK14-TnMinLAG. The resulting plasmids were sequenced (ACGT, Inc.) to verify successful religation.

To construct control plasmids expressing only Venus-TnpA (pJK14-venus-tnpA) and mCerulean3 (pJK14-mCerulean3) (35) the entire TE cassette was removed from pJK14-ISLEAD through digestion with I-SceI, dephosphorylation, and gel purification. The P_LtetO1-venus-tnpA fragment was amplified from pJK14-ISLEAD with Phusion Flash master mix and the primers I-SceI-P_LtetO1-venus F 5′-TTCCGACGTCTAGGGATAACAGGGTAATTTGACATCCCTATCAGTGATAGAGA-3′ and tnpA-I-SceI R 5′-GCTTGCATGCTAGGGATAACAGGGTAATTTATAGAGCTTTTGTTTGTAGGTTA-3′.

The fragment containing mCerulean3 and its reconstituted promoter was amplified from pJK14-ISLEAD using the primers I-SceI-P_lacIQ1-mCerulean3 F 5′-TTCCGACGTCTAGGGATAACAGGGTAATCATTTACGTTGACACCACCTGTAACGTATGGCATGATAGCGCCCGGAAGAGAGTCAATTCAGGGTGGTGAATATGGTGAGCAAGGGCGGGAGCTGT-3′ and mCerulean3-I-SceI R 5′-GCTTGCATGCTAGGGATAACAGGGTAATTTACTTGTACAGCTCGTCCATGCCG-3′.

Each amplified fragment was digested with I-SceI and ligated into the pJK14-ISLEAD backbone to generate pJK14-venus-tnpA and pJK14-mCerulean3, respectively. To control expression of Venus-TnpA, pJK14-tnpA was transformed into and assayed with strain CZ071, the kind gift of Ido Golding, Baylor College of Medicine, Houston, which is a K-12 MG1655 strain that constitutively expresses tet repressor.

Microscopy and Image Analysis.

To measure the TE excision response functions shown in Fig. 2, MG1655 Δlac nth <P_lacIQ-mCherry> cells carrying the indicated version of the TE were grown overnight in LB + 25 μg/mL kanamycin. The optical density at 600 nm (OD₆₀₀) of this culture was measured with a Bio-Rad SmartSpec Plus spectrophotometer, and an appropriate volume of the culture was added to M63 minimal medium + 0.5% (vol/vol) glycerol + 25 μg/mL kanamycin to yield a calculated initial OD₆₀₀ = 0.0002. The culture was partitioned in 5-mL aliquots to 20-mm glass test tubes, to which a variety of concentrations of aTc were added to titrate the cells with transposase inducer. These tubes were grown at 37 °C in a New Brunswick C76 water bath shaker with vigorous shaking until growth arrest at ∼OD₆₀₀ = 1.5–2.0; at this OD, the cells have undergone ∼12–13 doublings. Samples were then taken from each tube for imaging.

To perform fluorescent microscopy, 50-μL samples of culture were spread onto glass slides (Fisher Scientific Premium, 3 in × 1 in × 1 mm), covered with a no. 1.5 glass coverslip (VWR; 22 × 30 mm), and lightly compressed to seat the cells flat on the coverslip. The slide was placed on a Nikon Eclipse Ti-E fully automated inverted microscope with Perfect Focus System automated focus correction. The sample was maintained at 37 °C in a temperature-controlled environmental chamber. For each slide, 200 images in a 10 × 20 grid were taken using a Nikon CFI Apo TIRF 100× oil-immersion objective (N.A. 1.49) and captured using an Andor iXon Ultra 897 EMCCD camera with 100 or 300 ms exposure. Each image contains information captured from three fluorescent channels: mCherry, Venus, and mCerulean3. Fluorescent excitation was performed using HILO laser illumination (40, 41) at 561 nm (mCherry excitation; Coherent Sapphire 50 mW), 514 nm (Venus excitation, Venus-TnpA levels), and 457 nm (mCerulean3 excitation, excision reporting), in that order. Both 514-nm and 457-nm excitation were provided by a 40-mW Argon laser (CVI Milles Griot). Filter sets used were HQ560/55× ET645/75m (mCherry), ZET514/10× ET535/30m (Venus), and Z457/10× ET485/30m (mCerulean3). The sensitivity obtained using these optics is sufficient to detect single molecules of Venus-TnpA (41). We observed no anomalous aggregation of mCherry, Venus-TnpA, or mCerulean3 (40).

To directly quantify TE excision rates shown in Figs. 3 and 4, MG1655 Δlac nth <P_lacIQ-mCherry> cells carrying pJK14-ISLAG were grown overnight in M63 + 0.5% (vol/vol) glycerol + 25 μg/mL kanamycin. The OD₆₀₀ of this culture was measured (SmartSpec), and an appropriate volume of the culture was added to prewarmed M63 + 0.5% (vol/vol) glycerol + 25 μg/mL kanamycin to yield a calculated initial OD₆₀₀ = 0.0008. The cells were then grown at 37 °C in a water bath shaker with vigorous shaking until OD₆₀₀ = 0.05. 5 μL of this culture was then placed on an agarose pad cast on a glass slide. After allowing the agarose pad shape to stabilize for 20 min at 37 °C in a Fisher Scientific Isotemp incubator, the sample was covered with a no. 1.5 glass coverslip (VWR; 22 × 30 mm) and sealed with epoxy to prevent drying. Images consisting of 40–80 adjacent fields of view were taken every 20 min using the same imaging conditions as described above.

Images were analyzed using a custom image segmentation algorithm implemented in MATLAB. To correct for inhomogeneous illumination, images were first flattened by averaging the fluorescent intensity of each pixel over all 200 images for each slide; this averaged image was fit to a surface in 3D space and used to normalize all pixels in the image to the area of the image with the brightest illumination. Cell identification and image segmentation were performed on the flattened images using the red channel, where all cells are homogeneously fluorescent with high signal-to-background noise due to constitutive mCherry expression. For each identified cell, we recorded the area (in pixels), length of the major and minor axes of the cell (pixels), and the total fluorescence of the cell in each channel [arbitrary units (AU)], calculated as the sum of fluorescent intensities of all pixels that make up the cell.

Quantification of Plasmid Copy Number.

The average copy number per cell of pJK14 was determined through qPCR, using a Bio-Rad CFX96 Touch Real-Time PCR thermal cycler with SsoAdvanced Universal SYBR Green Supermix (Bio-Rad) and the following primers: pJK14-qPCR F 5′-TGCTAGACCCTCTGTAAATTCCGC-3′ and pJK14-qPCR R 5′-GGGTGCTACTTAAGCCTTTAGGGTT-3′.

These primers generate a 233-bp amplicon from pJK14 adjacent to the origin of replication. Optimum amplification conditions were determined by amplifying eight concentrations of a 10× dilution series of purified pJK14-ISLAG plasmid using two-step amplification with a thermal gradient of 50–70 °C. Amplification was performed in a 96-well hard-shell low-profile thin-wall skirted PCR plate (Bio-Rad). Optimum conditions were determined to be as follows:

1. 98 °C	3 min
2. 95 °C	10 s
3. 60 °C	30 s
4. GOTO 2	39×
5. 65–95 °C	Melting curve

These conditions generate an amplicon with T_m = 81.0 °C and efficiency ε = 96.8% [defined by $N\left(n\right)=N_0{\left(1+\epsilon \right)}^n$, where n is cycle number].

Average plasmid copy numbers per cell of uninduced pJK14-ISLAG, induced pJK14-ISLAG, and the control plasmid pJK14-mCerulean3 were determined by qPCR with the above primers and conditions. Overnight cultures of MG1655 Δlac nth <P_lacIQ-mCherry> pJK14-ISLAG and MG1655 Δlac pJK14-mCerulean3 grown in LB + 25 μg/mL kanamycin were diluted 5,000× into 20-mm glass test tubes with 5 mL M63 + 0.5% (vol/vol) glycerol + 25 μg/mL kanamycin. Then, 100 ng/mL aTc was added to one tube of MG1655 Δlac pJK14-ISLAG to induce expression of transposase. These three tubes were grown with vigorous shaking at 37 °C until OD₆₀₀ ∼1.5 (SmartSpec), and several samples were taken. One sample was used to generate eight concentrations of a 10× dilution series of cells for use in qPCR; at the same time, 10 other samples were diluted 10⁵× and spread onto 10 solid medium LB agar + 25 μg/mL kanamycin plates. These plates were incubated overnight at 37 °C. The number of colonies was counted the next day and averaged over 10 plates to determine the number of bacteria added to the PCR reactions.

Quantitative PCR was performed on each dilution series of cells with reactions performed in triplicate. In the same plate, a standard curve was generated in triplicate using purified pJK14-ISLAG plasmid with molarity determined by measurement of absorbance at 260 nm in a NanoDrop 2000c spectrophotometer (Thermo Scientific). The average number of plasmids per cell in each reaction was then calculated as

$$\langle \frac{N_{plasmids,i}}{N_{cells,i}}\rangle =\langle d_i\cdot \frac{{10}^{\frac{C_{t,i}-b}{m}}}{\langle N_{cells,i}\rangle }\rangle ,$$ [S1]

where d_i is the dilution factor of the ith sample ($d_i\in [{10}^0,{10}^7]$), m and b are the slope and y intercept of the standard curve respectively, C_t,i is the threshold cycle number of the ith sample, and N_cells,i is the number of cells added to the reaction, determined through plating as described above. The result is shown in Fig. S6, and error bars are the SEM.

Excision Verification and Quantification by PCR.

The initial verification of TE excision shown in Fig. 1C was generated with the primers Tn-junction F 5′-ACGTTACAGGTGGTGTC-3′ and Tn-pJK14 R 5′-CCAGAGGGCGCCCCAGCTGGCAATT-3′.

The primer Tn-junction F binds to the unique junction formed when the TE is excised from the plasmid. Together with primer Tn-pJK14 R, it generates an 858-bp amplicon only when the excised plasmid is present. To generate Fig. 1C, MG1655 Δlac pJK14-ISLAG was grown at 37 °C with vigorous shaking in two 20-mm glass test tubes with 5 mL M63 + 0.5% (vol/vol) glycerol + 25 μg/mL kanamycin. Then, 100 ng/mL aTc was added to one tube to induce transposase expression. After overnight growth, cells from each tube were diluted 100× and used as template in a colony PCR with primers Tn-junction F and Tn-pJK14 R. The templates were amplified using Phusion Flash master mix in a Bio-Rad S1000 thermal cycler with 70 °C annealing temperature and 15-s extension time.

The primers used for qPCR quantification of excision were Tn-qPCR F 5′-GGTGGTGCAGATGAACTTCA-3′ and Tn-junction R 5′-GACACCACCTGTAACGT-3′.

To determine optimal cycling conditions, 12 concentrations of a 10× dilution series were made by diluting purified pJK14-mCerulean3 in purified, undiluted, and unexcised pJK14-ISLAG plasmid, which simulates the mix of excised and unexcised plasmid one would expect in the experiment. Amplification was performed in a 96-well hard-shell low-profile thin-wall skirted PCR plate with a thermal gradient of 50–70 °C using SsoAdvanced Universal SYBR Green Supermix. Optimal conditions were determined to be:

1. 98 °C	3 min
2. 95 °C	10 s
3. 62.6 °C	30 s
4. GOTO 2	49×
5. 65–95 °C	Melting curve

These conditions generate a 215-bp amplicon from excised plasmid only with T_m = 89.5 °C and efficiency ε = 97.8%.

Quantitative PCR was performed using these cycling conditions on cells grown as described above (Quantification of Plasmid Copy Number) with tubes induced with 0, 5, 7, 10, 25, 50, and 100 ng/mL aTc. Because no detectable amplification was generated from the 0 aTc sample, the amount of excised plasmid per cell shown in Fig. 2C is quantified relative to the amount of excised plasmid measured in the 5 ng/mL aTc sample as

$$\frac{N_i}{N_5}=\frac{{\left(1+{\epsilon }_5\right)}^{C_{t,5}}}{{\left(1+{\epsilon }_i\right)}^{C_{t,i}}}\cdot \frac{\langle N_{cells,5}\rangle }{\langle N_{cells,i}\rangle },$$ [S2]

where ε₅ and ε_i are the efficiencies of amplification of the [aTc] = 5 ng/mL and [aTc] = i dilution series, respectively, C_t,i are the threshold cycles determined for each sample, and N_cells,i is the average number of cells added to the PCR as determined by plating and counting cfus from each sample as described above (Quantification of Plasmid Copy Number). In practice, ε₅ and ε_i are identical within error. Data shown in Fig. 2C are the averages of at least three experimental replicates, with error bars indicating the SEM.

Estimation of Absolute Venus-TnpA Concentration.

Estimation of the absolute number of transposase molecules was performed according to the method of Nayak and Rutenberg (42). By recognizing fluctuations from the mean bleaching kinetics of Venus-TnpA as binomial noise, the bleaching curves of individual cells can be analyzed to determine the constant of proportionality, ν, relating fluorescent intensity to the number of fluorescent molecules:

$$I=\nu N,$$ [S3]

where I is the fluorescent intensity of the cell and N is the number of Venus-TnpA molecules.

MG1655 Δlac nth <P_lacIQ-mCherry> pJK14-ISLAG cells were grown as described above and transposase expression was induced with 100 ng/mL aTc. At OD₆₀₀ = 1.0, cells were mounted on a slide and 500 fields of view imaged. Cells were imaged with the same conditions described in Microscopy and Image Analysis; however, 100 images of 10-ms exposure were taken in the yellow channel to record bleaching kinetics of each cell (Fig. S4). The cells in each image were identified and segmented using a custom MATLAB algorithm. In each image, only the bleaching kinetics of the cells in the region of the image with the brightest illumination were analyzed. For each cell, the total Venus-TnpA fluorescent intensity was calculated at each time point as the sum of intensities of all pixels that make up the cell divided by the area of the cell. The fluorescent intensity as a function of time normalized to the initial fluorescent intensity for each cell was then fit to an exponential decay curve to determine the decay constant, τ,

$$\frac{I\left(t\right)}{I_0}=\exp \left(-t/\tau \right).$$ [S4]

The mean decay constant calculated in this way from 419 cells was τ = 0.68 ± 0.01 s, and is shown as the black line in Fig. S4 A and B. Next, the variance of the bleaching curve for each cell from the mean bleaching kinetics was calculated as

$${\sigma }_i^2\left(t\right)={\left(I_i\left(t\right)-\langle I\left(t\right)\rangle \right)}^2=I_0\nu p\left(t\right)\left[1-p\left(t\right)\right],$$ [S5]

where ${\sigma }_i^2\left(t\right)$ is the variance of the ith cell at each time point t, $I_i\left(t\right)$ is the fluorescent intensity of the ith cell at time t, $\langle I\left(t\right)\rangle$ is the fluorescent intensity of the mean bleaching curve at time t, I₀ is the initial fluorescence of the cell, and p(t) is the fraction of unbleached molecules as a function of time. The variance as a function of the bleached fraction (1 – p) is therefore an inverse symmetric parabola centered at P = 0.5 (Fig. S4C). Integrating the equation with respect to p generates an estimate of ν from each cell:

$$\begin{array}{c}{\displaystyle {\int }_0^{1}dp\hspace{0.17em}{\nu }_{i}p\left[1-p\right]}={\displaystyle {\int }_0^{1}dp\frac{{\sigma }_i^2}{I_{i0}}}\\ \therefore {\nu }_i=6\cdot {\displaystyle {\int }_0^{1}dp\frac{{\sigma }_i^2}{I_{i0}},}\end{array}$$ [S6]

where I_i0 is the initial fluorescent intensity of the ith cell at t = 0. The constant of proportionality between fluorescence and number of molecules is then determined as the ensemble average of ν_i obtained from all cells,

$$\nu =\langle v_i\rangle ,$$ [S7]

or, equivalently, as the area under the parabola best fit to the mean normalized variance in Fig. S4C. We find ν = 130 ± 10 from 419 cells.

Compared with the doubling time in M63 minimal medium with glycerol as carbon source (∼120 min), the maturation time of Venus is extremely rapid, ∼7 min (36, 54). Correcting the estimated TnpA concentration for maturation increases the estimated number of molecules by only ∼5%; we therefore neglect this correction.

Simulation of Blue Fluorescence as a Function of Plasmid Excision and Cell Growth.

Because plasmid copy number can fluctuate over the lifetime of a single cell as a result of replication, the relationship between number of excised plasmids and the total blue fluorescence of the cell is potentially complex. We therefore performed simple simulations of cell growth and division to determine if the final mCerulean3 fluorescence level is proportional to the average number of excised plasmids per cell (Fig. S5A). The simulation assumes that the total cellular fluorescence is proportional to the number of mCerulean3 molecules inside a cell; mCerulean3 is expressed at a constant rate per TE-excised plasmid; and the number of mCerulean3 molecules is halved when a cell divides. The 2D-projected area of a cell increases at a constant rate and is halved upon division. Also in the simulation, each plasmid gets replicated only once at a uniformly random time point within a cell cycle (52, 53), and one of the two resulting plasmids has a probability to be excised if the template plasmid had unexcised TE. This excision probability is fixed over the lifetime of a single cell, but is chosen randomly for each cell to result in a distribution of final excised plasmid numbers. A cell keeps only one of the two resulting plasmids, and the other plasmid is passed on to the other daughter cell. Total plasmid number fluctuates between 8 and 16, giving an average copy number of 12. The final time point, which corresponds to the point of imaging, is a uniformly random time point between the 12th and 13th cell division. A total of 10,000 cells were simulated in this manner. This simulation concludes that the mCerulean3 fluorescence level at the point of imaging is expected to be proportional to the excised plasmid number (Fig. S5B).

Luria–Delbrück Modeling.

To explain the data in Fig. 4A, we made a model of a two-step process. This model is itself stochastic and we do not attempt to solve it exactly but instead simulate the distribution it produces and compare it to the experimental distribution in Fig. 4A. Before we can model the excision process, it is necessary to consider the distribution of colony sizes (cells per colony). We generate a new dataset of colony sizes by sampling with replacement (bootstrapping) from the experimental colony size data.

In the first step of the model, we construct a family tree for each colony in the bootstrapped dataset. We assume each colony starts from one individual that grows and divides until it reaches the final size of the colony, and we assume that the growth rate is constant over time. Thus, the family tree for a colony is the shallowest one possible. After each division, daughter cells have a heritable change occur with probability p_h. All descendants of a cell with this heritable change will also have it, and two sister cells from the same mother do not affect each other. The model makes no assumptions about the biophysical nature of this heritable change.

In the experiment, the blue flashes indicating transposon excision occur after growth stops. Therefore, in the second step of the model, after growth and division, any cells with the heritable change have excisions occur with a probability p_e.

To find the values of the parameters of the model that best explain the experiment, we simulated the model for parameter values in a small grid. The summary statistics of the SEM and SE of the SD were used to compare the mean event densities and SD of event densities between theory and data; the fit was considered good if the theory was within the SE of both the mean and the SD, and acceptable if within 2× the SE for both. The results shown as the red line in Fig. 4A are simulations of the model with p_h = 0.045 per division and p_e = 0.65.

Notice that if p_h = 1, the model collapses to the simplest model you might consider, which is that all events are independent of each other in space and time and obey a Poisson process. The distribution of event rates is not that of a Poisson process for a fixed colony size, however, because colony size varies. The distribution of event rates for a Poisson process with a rate equal to the experimental rate is shown in Fig. 4A in green. This distribution is transparently incorrect.

One can also consider the possibility that p_e = 1, which would correspond to a regular Luria–Delbrück process. Although visually this fit is less accurate than the two-step model, it is not obviously incorrect. Consequently, we compare the two models using the Akaike information criterion (AIC). We approximate the probability of the data given a model from a histogram generated by the model using 20 bins of the same size over the range of values generated. Note that because we are simulating the models, the histograms will vary slightly from simulation to simulation. A total of 100,000 colonies were simulated to generate the histograms. Comparing the two models’ fits, we find $\mathrm{\Delta }AIC=-80$, which corresponds to a probability of the two step model being the correct choice over a purely Luria–Delbrück process equal to ∼1 (within floating point error).

Pair Correlation Function g(r).

The pair correlation function, g(r), is a measure of the probability of finding an event (i.e., a blue fluorescent burst) at a distance r away from any other event. The event density at a distance r from any given reference event can be calculated as ρ(r) = ρg(r), where ρ = N/A is the average event number density in an entire colony of area A. For a random, homogeneous distribution of ideal particles, such as an ideal gas, g(r) = 1.

To calculate g(r) for a colony, each event in the colony is taken in turn as a reference particle. For each reference particle we calculate the pair correlation function g_i(r) for all r,

$$g_i\left(r\right)=\frac{1}{\rho }\cdot \frac{N_r}{2\pi r\cdot f_r\cdot \mathrm{\Delta }r},$$ [S8]

where N_r is the number of events between two rings a distance r and r + ∆r away from the reference particle. For the data presented in Fig. 3H, we take ∆r = 0.32 μm. To correct for edge effects, f_r is the fraction of the ring area that intersects the colony. We then calculate the colony pair correlation function g(r) as the ensemble average of g_i(r),

$$g\left(r\right)=\langle g_i\left(r\right)\rangle .$$ [S9]

Colony and g(r) Simulations.

Deviations of g(r) from that of a random distribution of ideal particles can arise from mundane physical sources. For example, g(r) for a random distribution of hard spheres in a low-density gas shows a peak at short distances, very similar to that we observe in Fig. 3H purely as a consequence of entropic volume exclusion effects. However, an explicit theoretical calculation of g(r) for unusually shaped particles, such as highly dense and polydisperse spherocylinders representing an E. coli colony, is extremely difficult. Consequently, we performed simulations of E. coli growth into microcolonies combined with random distributions of TE events to determine the expected properties of g(r) arising from randomly spaced TE events within an E. coli colony.

Our simulations are a modified version of DiSCUS, an agent-based model by Goni-Moreno and coworkers (56, 57) to study horizontal gene transfer in E. coli. DiSCUS models each cell individually as a spherocylinder. The simulation is written in Python scripting language and uses the 2D physics engine pymunk as a wrapper for the physics library chipmunk (Howling Moon Software), which handles the semirigid body dynamics of the cells. The physics engine handles updating the forces and positions of the individual cells that arise from the environment and interactions with other cells. All of the cells are nonmotile but can be pushed around due to the growth of other neighboring cells. For the results discussed here, DiSCUS has been modified to remove horizontal gene transfer mechanisms and add transposable element events.

During each time iteration, the program first checks each spherocylinder to see if it is larger than a critical size. At the critical size, the spherocylinder divides into two smaller spherocylinders. After the cell division step the spherocylinders are elongated. If there is too much pressure on an individual cell it will stop growing until the pressure is reduced. Finally, the physics engine resolves the forces on the cells and updates the spherocylinder positions accordingly, following standard classical mechanics.

These simulations were used to generate 200 different microcolony morphologies, each starting from a single cell and ending upon reaching a size representative of those we observe in our experiments (∼300 cells with a diameter of ∼15–16 μm). After growth arrest, 15% of the cells within each colony morphology were chosen at random to undergo TE events, a rate representative of the average final number of affected cells in each colony we observe experimentally. We calculated g(r) resulting from each such random distribution of events within the 200 different colony morphologies, and repeated this process three times. Finally, the mean g(r) expected from a completely random distribution of TE events was calculated as the ensemble average of each such calculated g(r).

Discussion

Our goal is to begin the quantitative understanding of how TEs fundamentally function and behave in single live cells before understanding more complex systems. Placing the TE under an inducible promoter allows us to precisely control and determine how TE excisions respond to transposase concentration. Examining the bleaching kinetics of Venus-TnpA allows us to estimate absolute numbers of transposase proteins within individual cells, which improves upon previous studies that could only infer mean TnpA levels from the applied inducer concentrations. Though we use a synthetic tet promoter derived from an E. coli TE to express TnpA instead of the natural tnpA promoter, the transposase levels in any wild-type system will still sample from the same response function. That even this simple system exhibits complex dynamic behavior illustrates the necessity of using real-time single-cell measurements rather than population and time-averaged estimates of TE kinetics, a parallel to the way in which real-time single-molecule measurements have revolutionized our understanding of the rich dynamics hidden by population-averaged ensemble measurements (46). This quantification of genome plasticity in real time permits the development of a precise narrative of the role of TE activity in evolution and even epidemiology.

The single-cell response curves shown in Fig. 2 are consistent with existing molecular models of how TnpA binds to and excises the TE from the host DNA molecule (21). The response function displays qualitatively distinct behavior in the leading vs. lagging strand. Because the lagging strand of DNA is discontinuously replicated, the lagging strand leaves single-stranded DNA exposed while synthesis of Okazaki fragments is completed. Hence, it is more energetically favorable for the folded imperfect palindromic sequences recognized by TnpA to form in the lagging strand than the leading strand, where the energetically favored state is canonically base-paired double-stranded DNA (21). Consequently, the TE in the lagging strand is extremely sensitive to TnpA, with the first excisions occurring in the presence of only 1–2 TnpA dimers. Conversely, ∼10× higher TnpA numbers are required to initiate excision from the leading strand.

Real-time imaging allows us to track how TE activity varies from one cell to another within different colonies over time. We found that upon growth arrest, excision events are distributed nonuniformly within each colony. This nonuniformity can be described with a Luria–Delbrück process, suggesting that some stochastic, heritable trait predisposes a fraction of cells to TE activity. Additionally, the relative lack of excision activities observed near the edges of colonies may arise from local environmental variation, such as nutrient availability, between the edge and center of a colony. Together, these results demonstrate that the rate of TE excision is highly dynamic and depends upon the amount of transposase in the cell, the TE’s orientation within the genome, the growth state and life history of the host cell, and the cell’s local environment.

Though here we focus solely on excision, we note that because excision of a TE is required before reintegration, it is likely that integrations and the mutations they generate will occur with a rate that is dependent upon the excision rate measured here. Previous studies detecting transposition in vivo using time-averaged population-level methods have estimated the convolved transposition rates, i.e., the combined rates of both excision and integration, as a result of experimental or conceptual limitations in separating the two processes. Mating-out assays, for example, detect TE integration only into a conjugative plasmid which is then transferred to a virgin recipient strain for detection (47). These methods therefore only measure the combined rate of excision, integration to the plasmid, and conjugation of the plasmid merged together. From a mechanistic standpoint, excision and integration are two separate processes that should be understood independently. It is necessary to know excision rates independently of reintegration to understand how stable transposable elements are in the genome. Furthermore, an excision itself is a mutation carrying biological significance. Any genes carried by the TE will be lost, and if the TE has silenced a gene by interrupting it, then excision may restore its function.

One of the primary results of this work is the observed heterogeneity of TE activity rates in both space and time. In a sense, this is surprising; the design of the synthetic TE used here is extremely simple, and yet it shows complex spatial and temporal dynamics. Furthermore, since the fundamental experiments of Luria and Delbrück, the uniform randomness and homogeneity of mutation rates is frequently taken as a starting point for descriptions and models of mutation and evolution. However, as shown in Fig. 2, the activity of the TE is a direct function of the intracellular numbers of TnpA protein. Because it is well known that intracellular protein levels are strongly influenced by the cellular growth state (48), cell-to-cell and temporal heterogeneity in intracellular TnpA amounts and the resulting TE activity levels should perhaps be anticipated. Similar arguments can readily be made about any other mutational process that relies upon the activity of an expressed protein for its generation or repair—for example, the repair of nascent point mutations by the proteinaceous mismatch repair system (49).

It is difficult to draw direct and meaningful comparisons between our measurements of TE excision rates and previous measurements. Previously measured transposition rates (i.e., excision followed by reintegration) are on the order of 10⁻⁶–10⁻¹⁰ transpositions per cell per doubling (23), or transpositions per cell per hour (11), whereas the excision rates that we measure are several orders of magnitude greater. A variety of hypotheses can be proposed to reconcile these results. For example, it is possible that reintegration is extremely inefficient and only successful for a small fraction of excisions. However, we have observed that expression levels of Venus-TnpA in these and other longer time-scale measurements do not decrease over time, which suggests this is not the case. It is also possible that previous experiments underestimate TE activity rates as a result of insufficiently deep sampling, or the deleterious physiological effects of the TE leading to extinction of affected cells within the population. The reason for this discrepancy remains unclear and is a subject for future work.

Experimental Procedures

Detailed procedures for all constructs and experiments can be found in SI Experimental Procedures.

Strains.

Experiments were performed using E. coli K-12 MG1655 Δlac (41, 43, 50, 51) expressing the red fluorescent protein mCherry (37) from a strong P_lacIQ constitutive promoter integrated into the nth chromosomal locus located near the replication terminus (41, 50). Molecular cloning and plasmid manipulations were performed using DH5α as a host strain.

Plasmid Construction.

The low copy number plasmid pJK14 (38) was used to host the TE in all experiments. pJK14 has a pSC101 replication origin and is replicated unidirectionally, i.e., there is a well-defined leading and lagging strand. Plasmid copy number is tightly controlled through the positive feedback of the plasmid-encoded protein RepA (52). Additionally, pJK14 is actively segregated to daughter cells through the pSC101 par system (53).

Plasmid pJK14-ISLEAD was designed using Vector NTI software (Life Technologies) and synthesized de novo by GENEWIZ Gene Synthesis Services (GENEWIZ, Inc.). Variants including pJK14-ISLAG were generated through standard molecular cloning techniques, described in detail in SI Experimental Procedures.

Microscopy and Image Analysis.

To measure the TE excision response functions in Fig. 2, cells carrying the indicated version of the TE were grown overnight in Lysogeny broth (LB). An appropriate volume of the culture was added to M63 minimal medium + 0.5% (vol/vol) glycerol and 25 μg/mL kanamycin to yield an initial OD₆₀₀ = 0.0002. To these tubes, varying concentrations of aTc were added to titrate cells with inducer. These tubes were grown at 37 °C with vigorous shaking until OD₆₀₀ ∼1.5. At this point, samples were taken from each tube for imaging.

A Nikon Eclipse Ti-E fully automated inverted microscope was used for imaging. To generate the transposase response curves, cells were placed on a glass slide and squeezed with a coverslip to ensure that as many as possible were lying flat in the focal plane. For each slide, we took 200 images. Each image contains information captured from three fluorescent channels: mCherry (red), Venus (yellow), and mCerulean3 (blue), in that order. Fluorescent excitation was performed using HILO laser illumination (40) with 561nm (mCherry excitation; cell area), 514 nm (Venus excitation, Venus-TnpA levels), and 457 nm (mCerulean3 excitation, excision reporting) in that order. The 561-nm excitation was provided by a 50-mW Sapphire laser (Coherent); both 514-nm and 457-nm excitation were provided by a 40-mW Argon laser (CVI Melles Griot). Filter sets used were HQ560/55× ET645/75m (mCherry), ZET514/10× ET535/30m (Venus), and Z457/10× ET485/30m (mCerulean3). We observed no anomalous aggregation of mCherry, Venus-TnpA, or mCerulean3 (40), and the maturation times of Venus and mCerulean3 are both less than 10 min at 37 °C (36, 54, 55).

To directly quantify TE excision rates shown in Fig. 3, 5 μL of a MG1655 Δlac nth <P_lacIQ-mCherry> pJK14-ISLAG culture in exponential growth at OD₆₀₀ = 0.05 was placed on an M63 glycerol medium agarose pad containing the appropriate antibiotics, that was cast on a glass slide. The sample was covered with a glass coverslip and allowed to settle for 20 min before being sealed with epoxy glue to prevent drying.

For imaging, the slide was placed onto a Nikon Eclipse Ti-E inverted microscope. The sample was maintained at 37 °C in a temperature-controlled environmental chamber. Images consisting of 40–80 adjacent fields of view were taken every 20 min in each of three fluorescent channels: mCherry, Venus, and mCerulean3.

Image analysis was performed using custom image segmentation and analysis algorithms implemented in MATLAB (MathWorks). Cell identification and image segmentation was performed using the red channel, where all cells are homogeneously fluorescent with high signal-to-background noise ratio due to constitutive mCherry expression.

Quantitative PCR.

Average plasmid copy numbers per cell for uninduced pJK14-ISLAG, induced pJK14-ISLAG, and the control plasmid pJK14-mCerulean3 were determined by qPCR with a Bio-Rad CFX96 Touch Real-Time PCR thermal cycler using SsoAdvanced Universal SYBR Green Supermix (Bio-Rad). Cells were grown as described above for imaging. Once the appropriate density of each strain was achieved, samples were taken for plating to determine the number of cells added to each PCR.

qPCR was performed on each sample in triplicate. In the same plate, a standard curve was generated using purified pJK14-ISLAG plasmid with known molarity determined by measurement of absorbance at 260 nm in a NanoDrop 2000c spectrophotometer (Thermo Scientific). See SI Experimental Procedures for details.

To determine relative number of TE excisions per cell (Fig. 2C, large red points), qPCR was performed as described above on cells induced with different concentrations of aTc. See SI Experimental Procedures for details.