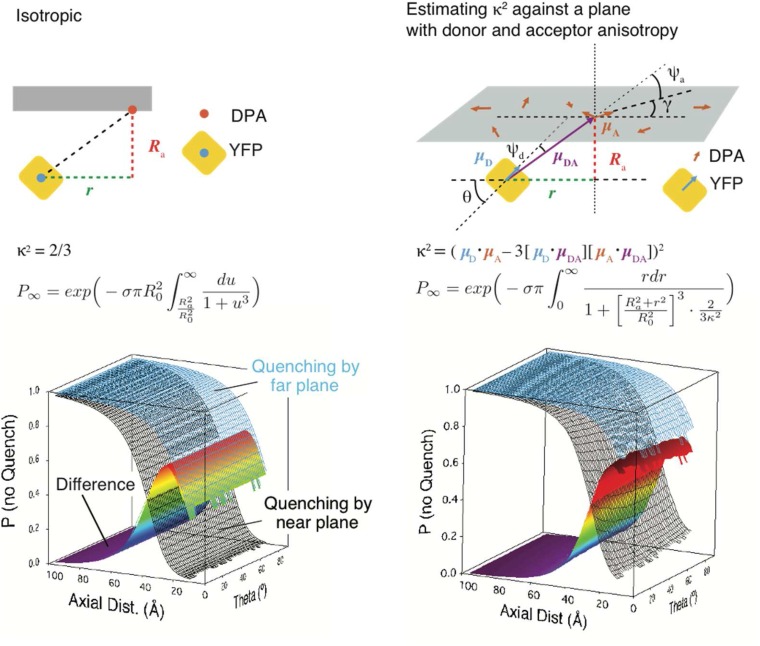
Fig. S8.

Isotropic and anisotropic treatments of FRET. Ignoring the dipole orientations of DPA and YFP leads to a simple 2D model of quenching (58). The substitution $u=(r^2+R_{\mathrm{a}}^2)/R_0^2$ was made. The theoretical quenching curves and their difference (equivalent to the curves in Fig. S6B) are plotted against a dummy variable, the orientation of the YFP dipole to the membrane plane (θ), for comparison with the anisotropic case. Considering the inclination of the YFP dipole (θ) to be fixed by steric factors and taking the DPA dipole to be randomly oriented (angle γ to the x axis) in the plane of the membrane forces calculation of the orientation factor κ. The donor vector (μ_D) is determined by θ, and the acceptor vector (μ_A) is determined by γ. Taking radial symmetry due to the random distribution of DPA, we consider μ_DA to be purely determined by the angle formed by r and R_a. The effect on the quenching curves as a function of axial distance (R_a) and donor dipole inclination (θ) is plotted. The major difference with the calculation of the isotropic case is that, for each function call during the numerical integration with respect to r, the average orientation factor κ was estimated from 200 random values of γ. The effect of anisotropy is limited to the effective decrease of R₀, which is more pronounced at low values of θ. This reduction eliminates the hump in the ∆F curve that is pronounced in our data.