Varying timescales of stimulus integration unite neural adaptation and prototype formation

Summary

Human visual perception is both stable and adaptive. Perception of complex objects, such as faces, is shaped by the long-term average of experience as well as immediate, comparative context. Measurements of brain activity have demonstrated corresponding neural mechanisms, including norm-based responses reflective of stored prototype representations, and adaptation induced by the immediately preceding stimulus. Here, we consider the possibility that these apparently separate phenomena can arise from a single mechanism of sensory integration operating over varying timescales. We used functional MRI to measure neural responses from the fusiform gyrus while subjects observed a rapid stream of face stimuli. Neural activity at this cortical site was best explained by the integration of sensory experience over multiple sequential stimuli, following a decaying-exponential weighting function. While this neural activity could be mistaken for immediate neural adaptation or long-term, norm-based responses, it in fact reflected a timescale of integration intermediate to both. We then examined the timescale of sensory integration across the cortex. We found a gradient that ranged from rapid sensory integration in early visual areas, to long-term, stable representations towards higher-level, ventral-temporal cortex. These findings were replicated with a new set of face stimuli and subjects. Our results suggest that a cascade of visual areas integrate sensory experience, transforming highly adaptable responses at early stages to stable representations at higher levels.

Introduction

Neural responses to stimuli are modulated by recent sensory history over varying timescales. On short timescales, neural responses are reduced if sensory input is similar or identical to preceding stimuli (i.e., neural adaptation [1]). At longer timescales, integration over many stimuli is required to generate “prototype” representations (the central tendency of sensory experience [2–4]). The presence of a prototype representation is inferred from the finding that the amplitude of a neural response reflects the distance of a stimulus from the center of a stimulus space (a “norm-based” response [4–6]).

These effects of sensory history have been measured separately in single unit studies in animal models [5–7] and in neuroimaging responses in humans [4]. They can seemingly co-occur, as for example both types of neural response have been observed to faces within macaque inferotemporal cortex [5–8] and the human fusiform gyrus [4, 6, 9]. While it is possible that neural adaptation and norm-based responses are manifestations of separate neural mechanisms that overlap at points of the visual hierarchy, we consider here the possibility that these neural responses represent the action of a single mechanism. Specifically, both neural adaptation and norm-based responses reflect the deviation of a current stimulus from a neural prior that is formed from stimulus history. Temporal integration that operates at an intermediate timescale might both manifest neural adaptation and generate a prior that produces apparent norm-based responses, with the degree of one effect or another depending on the intrinsic timescale of neural processing. We take as our inspiration recent work that has shown a hierarchy of timescales of integration in macaque cortex [10], and that norms are not stationary but continuously updated by experience [11].

We collected blood oxygen level dependent (BOLD) functional MRI data from fifteen subjects while they viewed a continuous stream of face stimuli. After characterizing the perceptual similarity of the faces, we modeled neural responses to the stimuli based upon an exponential integration of stimulus history (as has been observed in retinal ganglion cells [12]). Using this model, we can characterize the timescale of temporal integration in neural responses that show modulatory effects of stimulus history. We then tested if neural responses within the fusiform gyrus are better explained by separate neural adaptation and norm-based mechanisms, or if a single temporal integration mechanism can better account for the data. We also measured for each point on the cortical surface the time constant of temporal integration, and determined if there is a systematic organization to cortical responses as a function of our measure of temporal history (as has been found with other approaches [13]). Finally, we repeated the study with a different set of face stimuli and subjects to examine the replicability of our results.

Results

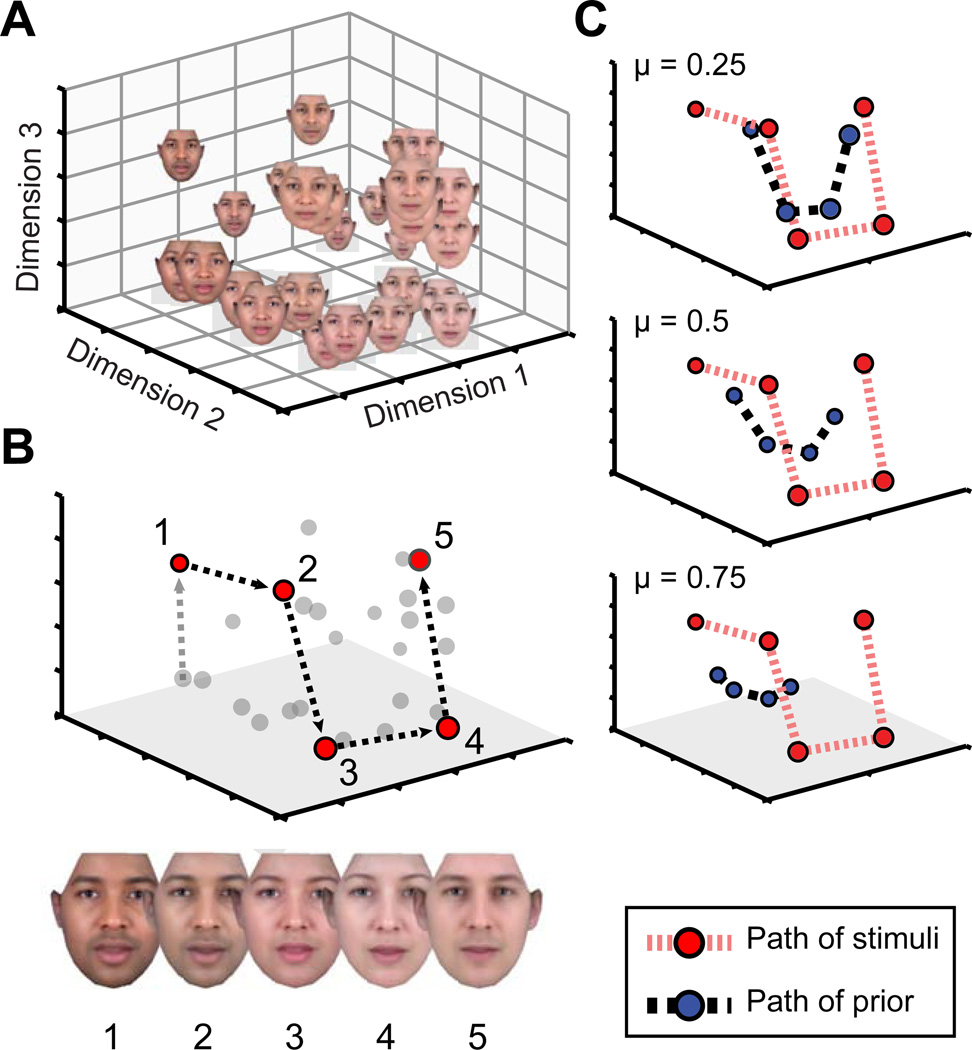
We measured neural temporal integration by obtaining fMRI responses to a set of 27 computer-generated faces. In separate behavioral studies, we assessed the perceptual organization of these stimuli and found that the mutual similarity of the faces is well described by three dimensions (Figure 1A, S1A). The Euclidean distance between any pair of faces within this space reflects the perceptual dissimilarity of the pair.

Figure 1.

Stimuli and neural modeling. (A) Synthetic faces varied in identity, skin tone, and gender (see Fig S1A). Behavioral ratings of pair-wise face similarity were used to obtain the three-dimensional perceptual similarity space via multi-dimensional scaling. (B) An example series of five stimulus presentations are plotted as a path through the perceptual similarity space. (C) A “prior” can be calculated as a function of the temporal integration parameter (μ) applied to the sequence of previous stimuli, and plotted as a point in the perceptual space. The prior will be shifted to a varying degree by each subsequent stimulus. Stimuli are integrated over longer durations for larger values of μ, and the prior stays close to the center of the stimulus space. For smaller values of μ the prior more closely tracks the path of presented stimuli. See also Figure S1.

We then considered the behavior of a neural system that is exposed to a series of faces. The sequential stimuli trace a path through the perceptual space (red points; Figure 1B). We propose that the system retains a memory of the weighted, average history of these stimuli. This neural “prior” is described as a point in the perceptual space. When a new stimulus is presented, the face is integrated into the running average and thus the prior is updated to a new position (blue points; Figure 1C).

In studies of retinal ganglion cells, the influence of past pulses of light upon the current state of the system is well described by a decaying exponential in time [12]. The exponential integration of cone input, for example, has a time constant of seconds and accounts for the perception of color after-images [14]. In such a system, a single parameter describes the degree to which the prior is updated by the presentation of each subsequent stimulus (here expressed as the temporal integration parameter μ; see Methods). For systems with μ close to one, the prior will equally weigh the entire history of stimuli, and thus tend to remain at the center of the stimulus space. For μ close to zero, the system has a shorter “memory”, and the prior is updated continuously to the location of the just-presented stimulus. A model with an intermediate temporal integration parameter will show an intermediate tendency for the prior to trail the sequentially presented stimuli.

To test this model of neural representation, we studied 15 subjects with functional MRI while they viewed a continuous, counter-balanced stream of stimuli [15] (Figure 2A). Subjects performed a continuous perceptual judgment task, but crucially this judgment regarded an aspect of the stimulus that was unrelated to its position within the perceptual space: the appearance of the face on each trial was randomly set to appear slightly older or younger in age, and the subject was asked to report this age appearance by button press. The age change was subtle (similarity ratings for young and old face sets were highly correlated: r = 0.95); mean accuracy across subjects was slightly, but significantly, above chance for this demanding attention task (mean 58% ± 2% SEM; chance 50%). Blank trials occurred in the stream of stimuli at counter-balanced intervals during which the subject withheld a response.

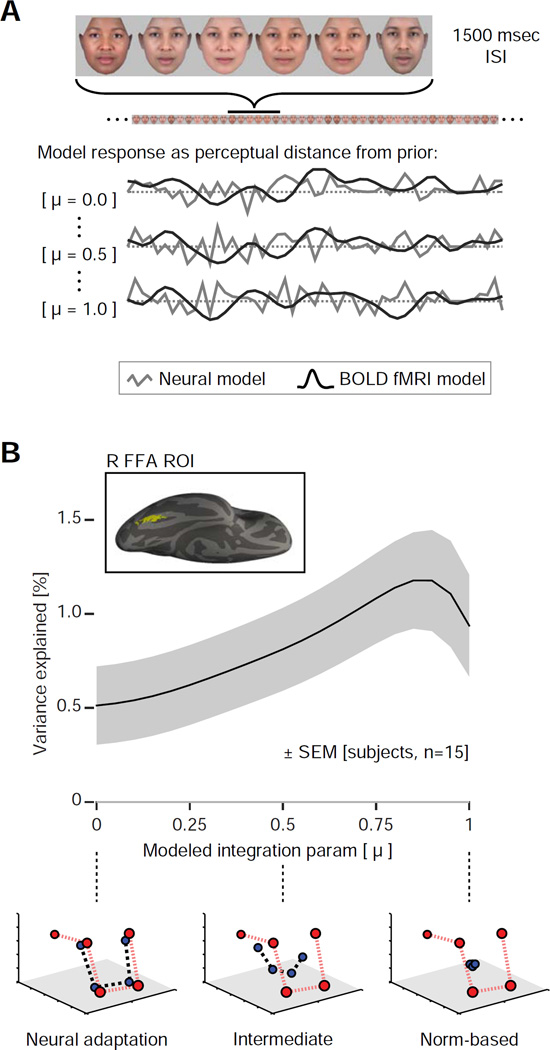
Figure 2.

Experimental design and ROI analysis. (A) During scanning, subjects observed a continuous stream of face stimuli while performing an unrelated attention task. Neural responses were modeled using continuous covariates that tracked the distance between the current stimulus and the calculated “prior” on every trial. A set of 21 models with different values of the temporal integration parameter (μ) were evaluated. (B) Average across-subject (n = 15) fit to the neural data for the range of models, within an across-subject, face-responsive region of interest (ROI) in the right fusiform gyrus (inset). The shaded region represents SEM calculated by bootstrap resampling across subjects. The peak corresponds to a model with an intermediate temporal integration parameter (μ = 0.85). The shape of this curve is dictated by the sampling of models on the x-axis, here a linear scale of μ. An alternative scaling based on the half-life of the underlying exponential is presented in Figure S3C. Schematics below the plot demonstrate the behavior of the prior for three representative values of μ. See also Figure S3.

In prior studies of neural adaptation, it has been found that the response to a stimulus is proportional to its dissimilarity from the immediately preceding stimulus [9, 16]. Separately, studies of norm-based coding have found that the response to a stimulus is proportional to its distance from the center of a stimulus space [4, 5]. These results can also be described as a neural response that is proportional to distance from a stored prior. Within this framework, tests for norm-based coding are sensitive to systems that show long temporal integration properties, while tests for neural adaptation are sensitive to systems that integrate over shorter timescales. A prior that integrates information over intermediate timescales would in principle show both of these modulatory effects.

We measured the influence of stimulus history upon neural response in our data. To do so, we created a family of models, each of which assumed a different time constant of a decaying exponential integration of the sequential face stimuli. We then modeled the neural response to each face as linearly proportional to the Euclidean distance between the continuously updated prior and the current stimulus, similar to a prediction error signal [17, 18], and convolved these neural models with a hemodynamic response function [19] to obtain predictors for effects within the BOLD fMRI data (Figure 2A). Importantly, the models with assumed temporal integration parameters of μ = 0 and μ = 1 correspond exactly to tests for one-back neural adaptation and norm-based coding, respectively. We confirmed in a series of simulations (Figure S2) that the temporal integration value measured using this approach is robust to variations in incidental aspects of the data, including variation in the shape of the hemodynamic response and nonlinearities in the transformation of neural response to BOLD signal.

Within the right fusiform face area (FFA) we measured the amount of variance that each model explained in the BOLD fMRI data as a function of the assumed temporal integration (Figure 2B). Across subjects, a significant amount of variance was explained by the model that assumed a μ of one (i.e., for which the prior is fixed at the center of the stimulus space), which could be interpreted as a norm-based coding response [variance explained: 0.94%, t(14) = 3.3, p = 0.005]. Essentially the same results are obtained if the norm-based effect is modeled as relative to the running average of all presented stimuli up to that point in the sequence, as opposed to being fixed in the center [variance explained: 0.91%, t(14) = 3.3, p = 0.005]. This illustrates that the central tendency of a random sampling of stimuli quickly converges upon the center of the stimulus space. Separately, we found that a significant amount of variance was explained by the model that assumed a μ of zero, which could be interpreted as a neural-adaptation effect [variance explained: 0.51%, t(14) = 2.4, p = 0.03]. These modulatory effects are reliable across subjects, albeit small (compared with an average of 6.0% variance explained by the main effect of the stimuli versus a blank screen).

Across the entire range of modeled windows of temporal integration, however, the best fit to the data was found for an intermediate parameter of μ = 0.85 [variance explained: 1.25%]. This implies that the influence of previously presented faces upon an updated neural prior drops by about half every 4 stimuli (Figure S3C) or 7 seconds (presuming an exponential integration function; considered in Figure S3). Importantly, a system that demonstrates this intermediate level of temporal integration gives rise to modulatory neural responses that can appear both as sequential neural adaptation and as norm-based responses.

Perhaps the FFA actually has separate neural mechanisms: one that implements a neural adaptation response relative to the last presented stimulus, and one that implements a norm-based coding response relative to a stored, central prototype. We used a cross-validation approach to test if this “dual mechanism” model better accounts for the BOLD fMRI data than a model with a single mechanism of intermediate temporal integration. The data from n−1 subjects were submitted to two analyses. First, an average, best fitting value for μ was derived (the single mechanism model). Second, the average parameter estimates for separate μ = 0 and μ = 1 covariates were obtained, and then used to construct a single covariate that combined both effects (the dual model). We then examined the variance explained in the reserved data from the nth subject. We observed that the proportion of variance explained by the single mechanism model was greater than the variance explained by the dual model (variance explained by a single mechanism model: 1.18% ± 0.27% SEM; variance explained by the dual model: 0.85% ± 0.26% SEM; difference paired t-test: t(14) = 3.4, p = 0.005). A left-hemisphere fusiform region showed the same effect (Figure S3B; variance explained by a single mechanism model: 1.24% ± 0.21% SEM; variance explained by the dual model: 0.96% ± 0.22% SEM; difference paired t-test: t(14) = 2.9, p = 0.0119). Similar results were also obtained when the test was conducted as the number of subjects with a better fitting model (in right FFA, the single mechanism model explains more variance than the combined model in 12 out of the 15 subjects; one-sided binomial test: p = 0.0176; in left FFA, the single mechanism model explains more variance than the combined model in 11 out of 15 subjects; one-sided binomial test: p = 0.0592). Therefore, not only is the single temporal integration model conceptually parsimonious, but it also provides a better fit to the data within the FFA.

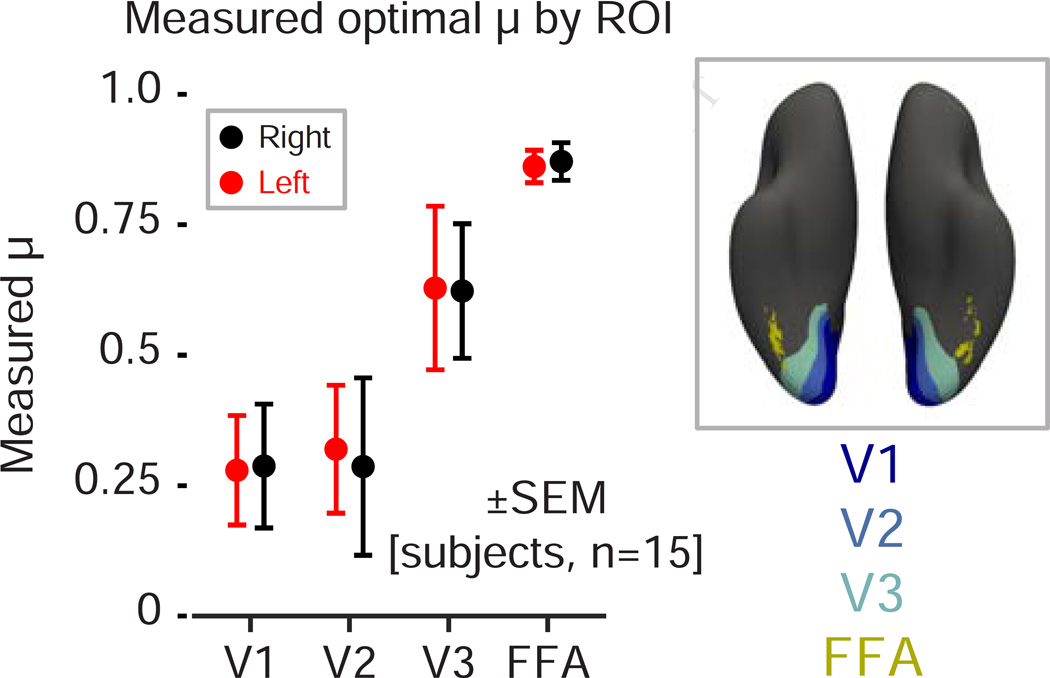
While the FFA is notable for having selective responses to faces, our stimuli evoke broad responses throughout the ventral visual cortex as compared to the blank trials. The same measurement of temporal integration that we performed within the FFA region of interest may be conducted at other locations across the visual cortex. Prior studies have examined the relative sensitivity of visual cortex to information that varies on shorter or longer timescales and a gradient of temporal sensitivity is generally found, with the shortest timescale of representation present within the primary visual cortex [13, 20]. We defined areas V1–V3 using a surface-based anatomical template [21] and calculated the mean, across-subject temporal integration parameter that best fit the modulatory effect in these areas (Figure 3). We observed an increase in temporal integration along the visual hierarchy, with mean integration parameters ranging from μ = 0.29 ± 0.12 to μ = 0.62 ± 0.13 between areas V1 and V3, corresponding to half-lives of approximately 0.5 trial (~ 0.8 seconds) and 1.5 trial (~ 2.2 seconds), respectively (in contrast to μ = 0.87 ± 0.04 and a half-life of ~ 7.5 seconds in the FFA).

Figure 3.

Temporal integration in the visual hierarchy. Measured temporal integration parameter (μ) across subjects in V1, V2, V3 and FFA. We observed increasingly long temporal integrations along the visual hierarchy, ranging from μ = 0.29 ± 0.12 in area V1, μ = 0.62 ± 0.13 in area V3, and μ = 0.87 ± 0.04 in FFA. Means and standard errors were obtained by bootstrap resampling.

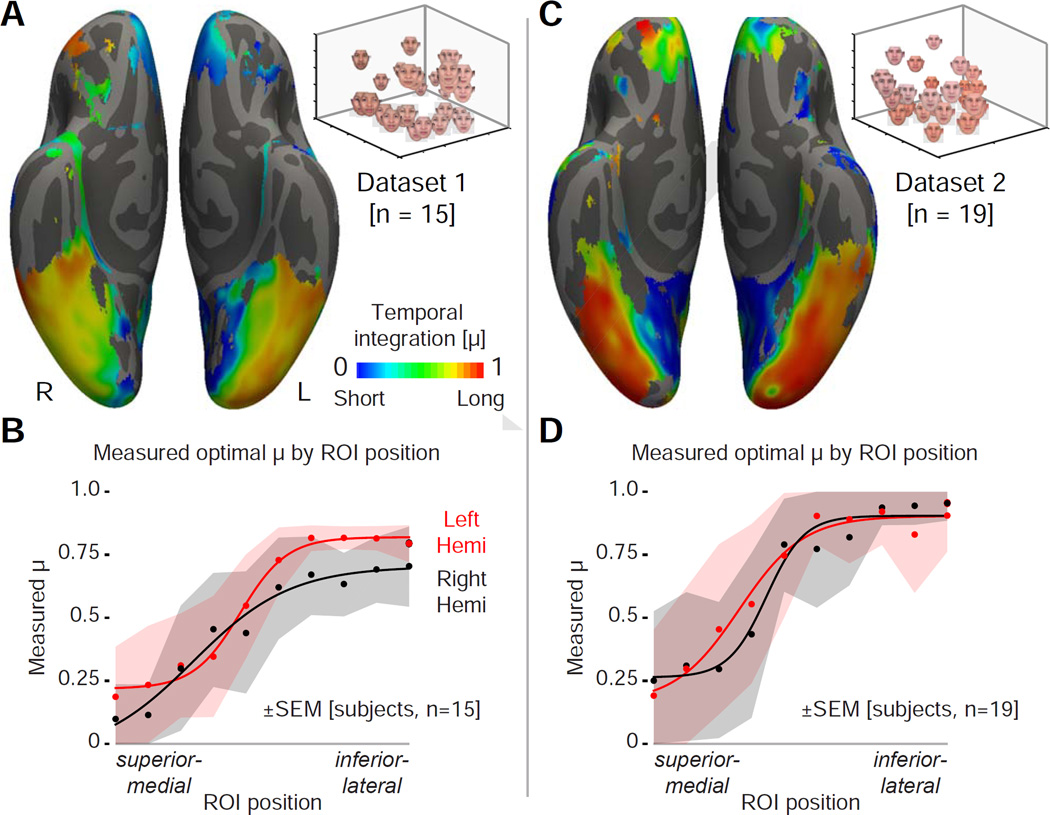
We then calculated the mean, across-subject temporal integration parameter, μ, that best fit the modulatory effect at each point on the cortical surface (constrained to those points for which the model explained more than 0.2% of the fMRI signal variance; Figure S4A). We observed a clear gradient of temporal integration across the cortical surface in both hemispheres (Figure 4A). In the medial and posterior areas of the visual cortex, values of μ close to zero were found, indicating a short temporal integration window and a modulatory effect consistent with immediate (1-back) neural adaptation effects. Moving inferiorly and laterally, the measured μ steadily increases, reflecting an ever-greater degree of integration of stimulus history, approaching norm-based effects of central tendency. Along a single trajectory (Figure 4B) the temporal integration value is found to be consistent across observers relative to the change across cortex. Across the surface of the cortex, variation in temporal integration is quite similar in the two hemispheres (correlation between hemispheres of the intersection of thresholded vertices on FreeSurfer-sym surface: r = 0.79).

Figure 4.

A gradient of temporal integration. (A) Measured temporal integration parameter (μ) across subjects at each cortical point that showed a modulatory effect of stimulus history (> 0.2% fMRI signal explained). White overlays indicate the points sampled in panel B. (B) Plot of across-subject average, regional μ from the set of sampled points ranging from superior-medial to inferior-lateral. Data points fit with a four-parameter sigmoid function. Means and standard errors were obtained by bootstrap resampling. (C–D) The corresponding measures from a second, independent dataset. See also Figure S4.

We tested if this result is reproducible and can be generalized beyond our initial stimuli. We collected a separate dataset from 19 subjects using a different set of face stimuli that varied in skin tone, aspect ratio, and internal facial features (Figure S1E). Measures of perceptual similarity again suggested a three-dimensional perceptual space (Figure S1F, G). We repeated the fMRI experiment and analysis. The proportion of variance explained by the single mechanism model was greater than the variance explained by the dual model in the left FFA (variance explained by a single mechanism model: 1.18% ± 0.24% SEM; variance explained by the dual model: 1.00% ± 0.27% SEM; difference paired t-test: t(18) = 2.3, p = 0.0352), but not in the right FFA (variance explained by a single mechanism model: 0.95% ± 0.25% SEM; variance explained by the dual model: 0.95% ± 0.27% SEM; difference paired t-test: t(18) = 0.05, p = 0.9643). When the test was conducted as the number of subjects with a better fitting model, the single mechanism model explained more variance than the combined model in 13 out of the 19 subjects (one-sided binomial test: p = 0.0835) within both the left and right FFAs (Figure S3E). A cortical gradient of temporal integration was also found in this dataset (Figure 4C), replicating our initial finding. The pattern of temporal integration values across the cortex (Figure 4D) was similar between hemispheres in this dataset (correlation between hemispheres of the intersection of thresholded vertices on FreeSurfer-sym surface: r = 0.82), and similar to that found in our first dataset (correlation between datasets of the intersection of thresholded vertices: r = 0.69).

Discussion

Our study begins with the observation that a single temporal integration mechanism could theoretically produce both short-term adaptation and norm-based responses, as each phenomenon reflects the similarity of a current stimulus to a continuously updated neural prior. Based upon work in retinal ganglion cells [12] we assumed an exponential integrator, which is characterized by a single parameter. Our empirical results demonstrate that neural responses to faces within the FFA are better described by this single mechanism operating over intermediate timescales, as opposed to separate adaptation and norm-based responses. We previously demonstrated that adaptation and norm-based responses can be confounded in measurement, and have proposed analytic techniques to estimate their separate influence [22]. Here we test our prior assumption that the two effects reflect separable processes, and instead find that they can be manifestations of a single underlying mechanism.

We note that our findings do not challenge the existence of stable, norm-based representations of faces, which are supported by a wealth of empirical neural [3, 4, 23] and behavioral [2, 11] results. We do find an intermediate degree of temporal integration in the FFA, suggesting that responses that appear norm-based at this location reflect a prior that is subject to modification on a time scale of seconds to minutes. In other regions, particularly more anterior and lateral in the ventral temporal lobe, we find temporal integration parameters that approach μ = 1, consistent with stimulus representations that are stable over longer timescales. Indeed, within the right FFA for our second dataset, we cannot reject a pure, norm-based mechanism on the basis of average variance explained (Figure S3E). Relatedly, we do not have imaging signal available from the most anterior portions of the temporal lobe (Figure S4A, C); it is possible that these sites contain stimulus representations that are stable on a time scales of months to years. We note as well that our stimulus sequences are not designed to address the subtle question of norm-based versus exemplar coding [24].

We view our results instead as an explanation for the emergence of new prototype representations at the center of a previously unseen stimulus space [25] and for the updating of existing prototypes [11], without the need to invoke a qualitatively novel system of temporal integration. Under our theoretical framework, any relatively long temporal integrator will construct a neural prior near the center of a perceptual space after presentation of a few randomly selected stimuli. This accords with experimental demonstrations of norm-based effects that vary during measurement of neural response [5, 6] or behavior [26]. Prior work on cortical timescales has measured autocorrelations [27] or the dependence of neural response on stimulation duration [13]. Here we quantify the effect of stimulus history relative to a specific temporal integration function, and again find a cortical gradient [13, 20]. While the gradient we observe does not perfectly align with the position of visual areas, we do find ever-longer timescales of neural integration towards ventral occipito-temporal cortex. In agreement with theoretical models [10] and electrophysiologic studies in primates [27], we expect that sequential cortical areas act as a cascade of temporal integrators to represent stable properties of the visual environment. We observe in our data as well some alignment of the gradient with the eccentricity axis of visual cortex, with shorter temporal integration at greater eccentricities. Perhaps relatedly, psychophysical and retinal ganglion cell sensitivity is also shifted to shorter temporal integration at greater eccentricities (e.g., [28]). We consider it an intriguing possibility that early specialization in the visual pathway gives rise to variation in temporal integration across the cortex.

Our analysis assumes an exponential form for integration. In simulations (Figure S2), we find that our approach (assuming an exponential form) accurately recovers relative temporal integration for other monotonically decreasing functions (e.g., linear; or power law [29, 30]). We view a key finding of our work to be the superiority of a single-mechanism model within the fusiform face area. We concede that demonstrating this superiority over one dual-mechanism model does not disprove all possible multi-mechanism models that combine varying timescales, though we feel any such proposals must now justify added mechanisms. We are receptive to the possibility that another single temporal integration function could provide a still-better fit to the data, and note that any such function would also have the property of being superior to the dual-mechanism alternative tested here. Different functions would lead, however, to different quantitative interpretations of an integration parameter in units of seconds or stimuli. Relatedly, we cannot determine from our data if the integration function is indexed by stimuli, seconds, or some combination. In single-unit studies in early sensory systems (e.g., the fly H1 visual neuron or mouse retinal ganglion cell [31, 32]), integration varies with the timing of stimulus changes, and thus is more reflective of stimuli than seconds. Further, it is possible to interpret the neural “prior” in our approach as a rolling sensory prediction and the modeled response as an error signal. It could be that the exact form of the integration function is related to the minimization of free energy [33]. Future studies could employ the approach we have described here to examine the effects of stimulus spacing and duration upon measures of temporal integration to directly address these questions.

Overall, our results demonstrate that varying timescales of stimulus integration are present across the cortex and can account for different modulatory effects of stimulus history. While a parsimonious explanation for some effects, there are phenomena that do not fit within our account. Most notably, our model does not easily accommodate the modulation of neural response produced by identical repetitions of a stimulus after multiple intervening stimuli [7, 34]. These effects can persist not only across stimuli, but across sessions [35] and days [36]. There is evidence that this “long-lag” repetition response arises from a different mechanism than the “short-lag” response that is the primary focus of the current work [34, 37, 38]. Such a dichotomy also manifests behaviorally. For instance, while orientation judgments are biased away from “short-lag” sensory history established on a timescale of seconds to minutes, judgments are biased towards “long-lag” sensory history [39]. We consider it likely that the integrated representation of recent stimulus history we have characterized here co-exists with additional neural mechanisms for the learning, identification, and comparison of visual objects.

Our work is part of a growing set of studies that find a distributed, hierarchical organization of temporal integration across the cortex [10, 13, 20, 27]. Here, we bring the idea of a hierarchy of timescales into contact with a well-established literature on neural adaptation and norm-based coding, showing that the intrinsic timescale of a cortical region predicts the degree to which it exhibits norm-based responses. Flexible access of this temporal hierarchy could be the mechanism by which visual behavior is both sensitive to novelty and captures the stability of visual experience.

Experimental Procedures

Stimuli and Experimental Design

Synthetic faces were generated with GenHead v1.2 (Genemation) using 3 primary axes with 3 points along each axis, resulting in 27 distinct stimuli. For Dataset 1, the three axes were gender, skin tone, and internal facial features, and for Dataset 2, skin tone, aspect ratio, and internal facial features (Figure S1A, E). All stimuli were created in a slightly older and younger version (a slight change in the skin texture and internal features in the stimulus generation software); this fourth dimension was used in an attention task. Stimuli (subtending 5°×5° of visual angle) were presented in a counterbalanced order [15] of 1624 trials. Each trial lasted 1500 ms (1400 ms stimulus, 100 ms blank screen); blank trials (with no stimulus) were doubled in length to 3000 ms. On each stimulus trial, the presented face was randomly set to appear in the older or younger version. Subjects were directed to judge the age of each face and respond with a bilateral button press, and received several minutes of training with example old and young faces prior to scanning.

Data Collection

A total of forty-one subjects were scanned for Dataset 1 (20 subjects) and Dataset 2 (21 subjects). From Dataset 1, 3 subjects were excluded for excessive head motion (recurrent transients of pitch > 2°), 1 because of loss of the behavioral data, and 1 due to poor performance in the cover task (> 15% trials with no response), leaving a total of fifteen subjects (10 female, 12 right handed), aged 19–25 years. From Dataset 2, 2 subjects were excluded for excessive head motion (recurrent transients of pitch > 2°), leaving a total of nineteen subjects (7 female, 15 right handed), aged 19–35 years. All subjects underwent magnetic resonance imaging on a 3.0-T on a Siemens Trio equipped with an 8-channel head coil. All subjects provided written informed consent and the study protocol was approved by the Institutional Review Board of the University of Pennsylvania. Echo-planar images (time repetition [TR] = 3 sec, time echo [TE] = 3 ms, voxel size = 3.00 mm isotropic, 64 × 64 in-plane resolution, 45 axial slices) were acquired during 6 scans (duration 408 sec each, final scan 396 sec). An MPRAGE image from each subject was reconstructed in surface space and mapped to the fsaverage template using FreeSurfer; functional data were transformed to the surface space and smoothed with a 10mm FWHM kernel. The fusiform region-of-interest (ROI) was defined by a group contrast of the main effect of stimuli versus blank screen, cropped using the FreeSurfer fusiform label, and narrowed to the top 400 vertices (approximately 400 mm² of surface area). ROIs for visual areas V1, V2, and V3 were defined using an atlas of cortical surface topology [21].

General Linear Model

Statistical analyses were performed upon the time-series data from each subject after removing the effects of covariates of no interest by regression. The covariates of no interest included: a main-effect covariate modeling the mean response to all face stimuli as compared to the blank trials and its temporal derivative; a covariate modeling the effect of a stimulus following a blank trial and its temporal derivative; six rigid-body motion parameters; and motion outliers. The effect in the data of an identical stimulus repetition and its temporal derivative was also removed. This correction was motivated by the observation that perfect stimulus repeats produce responses that are non-continuous with even small stimulus changes [15, 16].

The average residual time-series within each region of interest (V1, V2, V3, and the fusiform area) was modeled with a set of modulation regressors. Each modulation regressor was constructed using the measured, three-dimensional perceptual similarity of the sets of faces (Figure 1A, S1) and an assumed temporal integration parameter (μ). The neural response to the face presented on each trial was modeled as linearly proportional to the Euclidean distance of that face from a continuously updated prior. A Euclidean distance metric was assumed as the dimensions of face variation are perceived as integral [40]. The prior was positioned at the center of the stimulus space for the first trial, and the position of the prior on each subsequent trial (t) was given by:

$${\mathit{r}}_t={\mathit{r}}_{t-1}+(1-\mu )({\mathit{s}}_t-{\mathit{r}}_{t-1})$$

where r_t represents the coordinates of the position of the prior within the three-dimensional perceptual space on trial t, r_t−1 is the position of the prior in the previous trial, s_t is the position of the current stimulus, and μ is the time constant scaled between zero and unity. The fMRI BOLD time series was modeled using a set of regressors with values of μ ranging from 0 to 1 in steps of 0.05. Each covariate was mean centered, and convolved with a canonical hemodynamic responses function [19], and scaled to have unit variance.

Whole Brain Mapping

For each of 21 values of μ, we combined the individual surface maps from each of the six scans for a subject in their native surface space, and then combined these into a single group map after projecting the individual surface maps to fsaverage space with an additional 10 mm smoothing kernel (for the purpose of visualizing the low spatial frequency cortical gradient). The resulting group maps contained at each vertex the μ with the largest weight from the 21 possible. From this surface map, we cropped all vertices for which the temporal integration regressor with largest weight had a negative modulatory effect or where less than 0.2% of the total variance was explained (Figure 4A). To illustrate across-subject variation, 10 circular ROIs with a 2-vertex radius were plotted on the fsaverage surface in a continuous representative trajectory, running from area V1 to inferior occipito-temporal cortex. The mean and standard errors of μ within each of the 10 ROIs (and within the four regions of interest in Figure 3) were obtained by bootstrap resampling, with 10,000 samples from the subject pool with replacement.

Model description

Let r_t be the position of the prior at time t. Given a stimulus s_t presented at time t, s_t follows the update rule:

$${\mathit{r}}_t={\mathit{r}}_{t-1}+(1-\mu )({\mathit{s}}_t-{\mathit{r}}_{t-1})$$ (1)

i.e., the prior moves by (1 − μ) in the direction of s_t. Expanding this recursive expression, the position of the prior can be written as:

$${\mathit{r}}_t=(1-\mu ){\mathit{s}}_t+\mu (1-\mu ){\mathit{s}}_{t-1}+{\mu }^2(1-\mu ){\mathit{s}}_{t-2}+\cdots$$

We assume, without loss of generality, that the prior position at time t = 0 is in the center of the perceptual space, i.e. r₀ = 0. Thus, the position of the prior can be written as:

$${\mathit{r}}_t=(1-\mu )\sum _{i=0}^{t-1}{\mu }^i{\mathit{s}}_{t-i}$$ (2)

i.e., at each time step the stimulus influence on the prior position decays by a factor of μ. We can rewrite equation (2) as:

$${\mathit{r}}_t=(1-\mu )\sum _{i=0}^{t-1}{e}^{i\text{ ln}(\mu )}{\mathit{s}}_{t-i}=(1-\mu )\sum _{i=0}^{t-1}{e}^{-\lambda i}{\mathit{s}}_{t-i}$$

where we see that the stimulus influence on the prior position decays exponentially with rate λ = − ln μ. The half-life of this decay is given by:

$$t_{1/2}=\frac{\text{ln }2}{\lambda }=-\frac{\text{ln }2}{\text{ln }\mu }$$ (3)