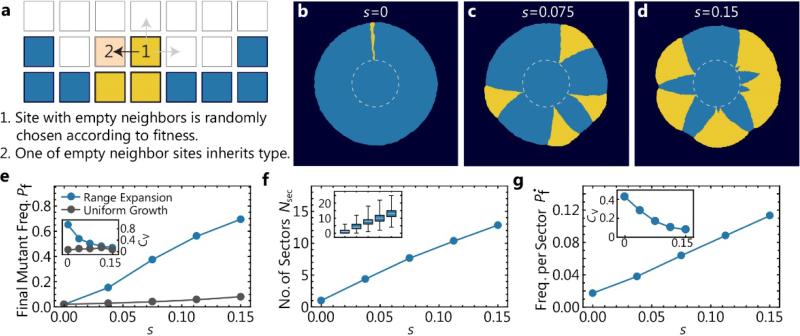
Fig. 2. Adaptation from standing variation emerging in a meta-population model of population growth.

(a) Illustration of the algorithm underlying our coarse-grained simulations (Methods). A lattice site at the population frontier is chosen and copied into an empty neighboring lattice site. The newly occupied site inherits the state of the parent site. (b-d) State of the lattice at the end of three simulations.

To mimic our experiments in Fig. 1, we initiated the expanding population as an occupied disk (dashed line) of radius R_i ≈ 550 such that a random fraction P_i = 0.02 of lattice sites is of the mutant type, and simulated until the final radius R_f ≈ 3R_i was reached. (e) Final mutant frequency P_f and corresponding coefficient of variation C_v (inset) as a function of selective advantage s determined in range expansions (blue, 500 simulations per condition) and corresponding simulations of uniform growth (gray, 3 simulations per condition, see Methods for algorithm) for the same parameters. Both final frequency and variation are larger for range expansions. (f) Number and standard error of mean of sectors at the end of range expansions as a function of selective advantage for the same simulations. Inset illustrates the spread of data points as a box plot. (g) Frequency per sector $P_{\mathrm{f}}^{\ast }$, calculated from colonies with only a single sector, which were simulated using a low initial mutant fraction P_i = 0.005.